Примеры решения задач

Задача 2.1. Через блок, массой которого можно пренебречь, перекинута невесомая и нерастяжимая нить. На ней висят два груза массой и соответственно. Пренебрегая трением, определить ускорение системы и давление на ось блока F.

На связанные нитью грузы действуют силы тяжести и сила натяжения нити как указано на рис. 2.1. Учитывая замечания п. 4 методических указаний, запишем II закон Ньютона в проекции на вертикальную ось, считая, что :

Рис. 2.1

Вычитая из первого уравнения второе, получаем . Отсюда

Найдём силу натяжения нити:

.

Очевидно, что при условиях невесомости блока давление его на ось .

З адача 2.2. Каков вес тела, имеющего массу , в вертикальном лифте, движущемся с ускорением ? Рассмотреть случаи и .

1. Лифт опускается с ускорением . Относительно ИСО тело движется с ускорением под действием силы тяжести и силы реакции опоры (рис. 2.2,а):

.

В данном примере вес (сила, с которой тело давит на опору) согласно III закону Ньютона равен по модулю силе опоры: , т.е. вес тела в этом случае меньше силы тяжести.

2. Лифт поднимается с ускорением. Теперь решим задачу относительно лифта – неинерциальной системы отсчета.

Рис. 2.2

В этом случае II закон Ньютона выполняется, если дополнительно ввести силу инерции как показано на рис. 2.2,б . Но относительно лифта тело покоится, тогда в проекции на вертикальную ось . И вес тела равен . В поднимающемся с ускорением лифте вес больше силы тяжести.

Задача 2.3. Сила зависит от времени по закону . Как изменятся импульсы и скорости тел массами  кг и кг, если такая сила будет действовать на каждое из них в течение с в направлении их движения?

По II закону Ньютона для первого и второго тела

(Нс).

Изменение импульса не зависит от величины самого импульса.

Найдем изменение скорости или . Тогда для первого тела м/с²; для второго м/с².

Задача 2.4. Оцените потери механической энергии пули массой кг, попадающей в висящий на нерастяжимой нити ящик с песком массой кг и застревающей в нем.

При неупругом ударе выполняется закон сохранения импульса в проекции на горизонтальную ось (рис. 2.3):

.

Откуда скорость ящика с пулей

.

Потери механической энергии происходят только в результате неупругого соударения, с учётом :

.

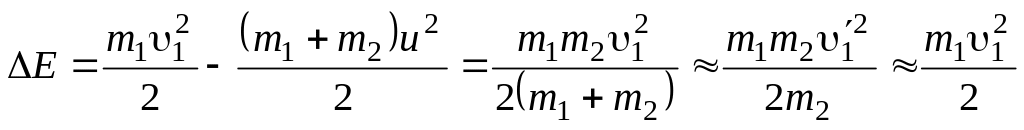То есть почти вся механическая энергия пули теряется.

Задача 2.5. Воронка имеет форму полусферы радиусом см и частично заполнена водой. Расстояние от поверхности земли до поверхности воды м. Какую работу нужно совершить, чтобы откачать воду на поверхность земли?

По мере откачивания воды высота, на которую поднимают очередную порцию, растет от до (рис. 2.4). При этом слой воды толщиной , который поднимают с глубины имеет массу

. (2.23)

Рис. 2.4

Работа подъема такого слоя равна приращению потенциальной энергии:

. (2.24)

Величины , зависят угла от следующим образом. Из рис. 2.4 очевидно, что

и . (2.25)

Взяв дифференциал от первого выражения в формуле (2.25), получаем

. (2.26)

Подставляем в (2.24) (2.23), (2.25), (2.26).

.

Итак, получаем интеграл по переменной , при этом нижний предел интегрирования равен , а верхний - ,

(кДж).

Задача 2.6. На наклонной плоскости с основанием b и углом наклона лежит груз массой , связанный нитью, перекинутой через блок, с другим грузом . Коэффициент трения между телом и наклонной плоскостью равен . Найти силу натяжения нити, ускорение грузов и время движения груза по наклонной плоскости.

Как показано на рис. 2.5, на груз , двигающийся вертикально, действуют сила тяжести и сила натяжения нити , на груз, находящийся на наклонной плоскости, – силы и , реакции опоры и трения . Направление последней силы заранее не известно, так как не известно, при каком условии первое тело будет двигаться вниз.

Рис. 2.5

Сила трения не может изменить направление движения, поэтому найдем условие соскальзывания первого тела без ее учета. Для этого случая уравнения движения первого и второго грузов имеют вид

.

Введем оси координат, как указано на рисунке. Спроецируем на них полученные уравнения, учитывая нерастяжимость нити и пренебрегая массами нити и блока :

_(2.27)

.

Первое тело будет соскальзывать с наклонной плоскости ( ) при условии .

Учтем теперь, что сила трения направлена в сторону, противоположную движению, и запишем II закон Ньютона для первого тела при наличии трения:

,

а в проекциях на oси

(2.28)

(2.29)

Решая совместно уравнения (2.27) – (2.29), с учётом , получим

Для соскальзывания первого груза с учетом трения достаточно выполнить условие

Отвечая на последний вопрос задачи, надо обратиться к законам равноускоренного движения . Отсюда время соскальзывания груза по наклонной плоскости длиной равно:

Отметим, что если выражение в квадратных скобках знаменателя равно нулю, то это соответствует состоянию покоя.

З адача 2.7. Муфта А массой  г может свободно скользить вдоль гладкого стержня, изогнутого в форме полукольца радиусом см. Систему привели во вращение с постоянной угловой скоростью об/с вокруг вертикальной оси ОО'. Найти угол , соответствующий устойчивому положению муфты, и силу реакции стержня для этого угла.

, (2.30)

. (2.31)

Учитывая, что модуль центростремительного ускорения и разделив первое уравнение на второе, получаем . Для угла находим соотношения:

а) – что соответствует положению равновесия (система покоится);

б) Подставим числовые значения: ; .

Модуль силы реакции опоры найдём из (2.31):

Н.

Задача 2.8. На горизонтальной плоскости лежит клин массой М. На грань клина кладут тело массой . Все поверхности соприкасающихся тел гладкие. Найти горизонтальные ускорения обоих тел и силу Р, с которой тело давит на клин.

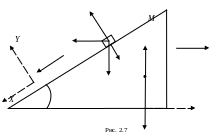
Рассмотрим сначала движение клина массой М относительно горизонтальной плоскости (рис. 2.7). На клин действуют силы тяжести , давления со стороны тела массой и реакции плоскости . Уравнение движения клина имеет вид:

.

Поскольку ускорение имеет лишь горизонтальную составляющую, введем ось Х₀ в направлении ускорения и спроецируем на нее полученное уравнение:

. (2.32)

Для нахождения силы Р рассмотрим движение тела массой . При этом в качестве системы отсчета удобно выбрать клин, который сам движется с ускорением , т.е. данная система отсчета неинерциальная. На тело массой в таком случае действуют силы тяжести , реакции клина и инерции . Уравнение движения тела имеет вид Спроецируем его на выбранные оси (х – в направлении ускорения , у – в перпендикулярном направлении):

(2.33)

. (2.34)

По III закону Ньютона искомая сила давления тела на клин равна:

. (2.35)

Решая совместно (2.33), (2.34), (2.35) и (2.32) получим

,

.

Горизонтальное ускорение а тела массой m относительно горизонтальной плоскости складывается из ускорения клина и проекции вектора на ось х (см. рис. 2.7):

.

Задача 2.9. Велосипедист едет по круглой горизонтальной площадке, радиус которой , а коэффициент трения зависит только от расстояния до центра площадки по закону , где – постоянная. Найти радиус окружности с центром в точке , по которой велосипедист может ехать с максимальной скоростью. Какова эта скорость?

Примем велосипедиста за материальную частицу, движущуюся по окружности в горизонтальной плоскости с центростремительным ускорением . Очевидно, что на тело действуют сила тяжести, сила трения и сила реакции опоры. Запишем уравнение II закона Ньютона:

.

В проекции на выбранные оси координат, согласно рис. 2.8, получим

Ох: ,

Оу: ,

,

т.е. Тогда ,

,

Рис. 2.8

очевидно, что . Скорость будет максимальной если а После дифференцирования получаем, что радиус окружности, при которой скорость максимальна, . Тогда максимальная скорость .

Задача 2.10. На покоящуюся частицу массы в момент начала действовать сила, меняющаяся со временем по закону , где – постоянный вектор, – время, в течение которого действует данная сила. Найти импульс частицы после окончания действия силы и путь, пройденный частицей за время действия силы.

Воспользуемся основным уравнением динамики материальной точки (II законом Ньютона):

,

тогда

,

с учетом заданного закона изменения силы получим

.

Проинтегрировав данное уравнение с учетом того, что в начальный момент времени частица покоилась, получим

,

при условии , . Скорость получим из импульса частицы :

.

Вектор скорости сонаправлен с постоянным вектором , поэтому модуль вектора скорости .

Путь, пройденный частицей за время , равен:

(м).

З адача 2.11. На покоящийся шар налетает со скоростью другой шар, одинаковой с ним массы. В результате абсолютно упругого удара двигавшийся шар изменил направление своего движения на угол . Найти скорость шаров после удара.

Для абсолютно упругого удара выполняются законы сохранения импульса (рис. 2.9) и энергии:

,

Из второго уравнения очевидно, что

. (2.36)

Уравнение закона сохранения импульса дает сумму двух векторов, модуль которого можно найти исходя из теоремы косинусов:

. (2.37)

Сравним (2.36) и (2.37). По условию задачи, очевидно, что и , тогда

, , .

Спроецируем уравнение закона сохранения импульса на выбранные оси с учётом :

Ох: ,

Оу: ,

.

Итак,

, .

Задача 2.12. Два тела с массами и прикреплены к нитям одинаковой длины и общей точкой подвеса. Тела отклонили на один и тот же угол в разные стороны и отпустили без толчка. Найти высоту, на которую поднимутся тела в результате абсолютно неупругого удара и тепловые потери механической энергии при этом.

При данном угле отклонения и длине нити очевидно (рис. 2.10), что

.

Движение тел вниз происходит без потерь механической энергии, поэтому

. (2.38)

Для абсолютно неупругого соударения справедлив закон сохранения импульса в проекции на ось х:

,

. (2.39)

Направление движения тел после удара зависит от соотношения масс и .

Можно считать, что движение тел на высоту не сопровождается потерей механической энергии, тогда

.

При абсолютно неупругом ударе механическая энергия не сохраняется, тогда

где – тепловые потери. С учётом (2.38) и (2.39)

.

Задача 2.13. Небольшое тело массой начинает скользить с высоты по наклонному желобу, переходящему в “мертвую петлю” радиуса . Найти вес тела и ускорение в точке, высота которой равна . На какой высоте находится точка желоба, из которой тело выпадает? Трением пренебречь.

В отсутствие силы трения уравнение движения тела по желобу имеет вид

.

Проецируя уравнение на выбранные оси (рис. 2.11), получаем систему

,

,

где проекция является центростремительным ускорением, а , соответственно, центростремительной силой.

Вес тела или сила давления тела на опору, по III закону Ньютона равен по модулю силе нормальной реакции опоры , т.е.

.

Как явствует из рис. 2.11 для точки 2 , тогда .

Теперь найдем скорость тела в точке 2. Отсутствие силы трения (неконсервативной силы) позволяет применить закон сохранения полной механической энергии. Поэтому энергия тела в первой и во второй точках равны:

таким образом,

.

Тогда вес тела

.

Полное ускорение тела в точке 2

,

где

,

.

Тогда

.

Теперь находим высоту точки 3, из которой тело выпадает. Геометрически , где – угол, определяющий положение точки на «мертвой петле». Проекция уравнения движения тела на ось в точке 3 имеет вид

Условие, когда тело покинет желоб, определяется т.е.

.

Согласно закону сохранения энергии, можно записать:

,

откуда

.

Тогда

, , а

т.е. при данных условиях тело не сможет пройти верхнюю точку “мертвой петли”.

Далее рассмотрим задачи на закон всемирного тяготения

Приведенные выражения для силы тяготения (2.20) и потен-циальной энергии гравитационного взаимодействия (2.22) справедливы тогда, когда расстояние между двумя телами много больше их линейных размеров. Если же тела обладают сферической симметрией (например, шар), то формулы справедливы при любых расстояниях между телами, но тогда равно расстоянию между центрами сфер.

Задача 2.14. Две звезды массами m и М движутся по окружности и находятся на неизменном расстоянии друг от друга. Найти периоды их обращения.

Первая звезда притягивает вторую силой (рис. 2.12)

,

сила, с которой вторая притягивает первую, равна:

. (2.40)

Р ис. 2.12

Запишем уравнение движения (II закон Ньютона) для каждой звезды, выразив центростремительное ускорение через период вращения:

(2.41)

. (2.42)

Приравняем полученные уравнения:

,

откуда, учитывая, что звезды находятся все время на одинаковом расстоянии друг от друга, т.е. получим

Из полученной системы найдём радиусы орбит

, . (2.43)

Для того чтобы определить период обращения подставим в уравнение движения первой звезды (2.41) выражение для силы тяготения (2.40):

.

Окончательно с учётом (2.43)

Задача 2.15. Тело, вращаясь по круговой орбите радиусом ( – радиус Земли), получает радиальный импульс, который сообщает ему дополнительную скорость направленную от центра Земли по радиусу. Каково должно быть минимальное значение дополнительной скорости, чтобы тело могло покинуть область земного тяготения?

На Землю и тело действуют лишь силы взаимного притяжения (действием других тел можно пренебречь), поэтому система «тело–Земля» замкнута и можно использовать ЗСЭ. Полная энергия тела на орбите радиусом R (благодаря тому, что масса Земли М много меньше массы тела т, пренебрегаем изменением кинетической энергии Земли) складывается из его кинетической энергии и потенциальной энергии взаимодействия :

Потенциальная энергия тела, покинувшего область земного притяжения, равна нулю, кинетическую энергию также можно положить нулевой, так как требуется найти минимальное значение дополнительной скорости, поэтому полная энергия в данном случае Из ЗСЭ

откуда

(2.44)

На орбите радиуса в момент сообщения дополнительной скорости тело приобретает скорость, модуль которой определяется (рис. 2.13)

(2.45)

– скорость движения спутника по стационарной орбите. Из уравнения движения (II закон Ньютона)

или ,

отсюда

(2.46)

Подставив соотношения (2.46) и (2.45) в (2.44), найдем

.

Для радиальной составляющей скорости получим

,

где – вторая космическая скорость.