
- •Л.И. Васильева, н.А. Иванова, д.Л. Федоров, с.Н. Соколова механика пособие к решению задач
- •1. Кинематика поступательного движения материальной точки. Кинематика вращательного движения абсолютно твердого тела Основные определения и формулы
- •Методические указания
- •Примеры решения задач
- •2. Динамика материальной точки Основные определения и формулы
- •Методические указания
- •Примеры решения задач
- •3. Динамика твердого тела Основные определения и формулы
- •Методические указания
- •Примеры решения задач
- •Законы сохранения момента импульса и энергии
- •Примеры решения задач
- •Поступательного и вращательного движений
- •Механика
- •190005, С.-Петербург, 1-я Красноармейская ул., д.1
Методические указания
Решение задачи необходимо начинать с выбора системы отсчета, которая включает в себя тело отсчета, систему координат и часы. Следует помнить, что в классической механике пространство и время «абсолютны», т.е. масштабы длин и промежутков времени не изменяются от одной системы к другой.
Следует уяснить из текста задачи, о каком способе описания движения материальной точки идет речь. Существует три способа: а) векторный, когда закон движения, определяющий положение точки, задается уравнением r = r(t), где r – радиус-вектор исследуемой точки, проведенный из неподвижной точки О выбранной системы координат; б) координатный, когда закон движения, например, для декартовой системы координат задается уравнениями: х = х(t), y = у(t), z = z(t), где х,у,z – проекции радиуса-вектора точки на оси координат относительно начала координат в момент времени t; в) траекторный, когда закон движения задается уравнением s = s(t). При этом известны траектория движения, точка начала отсчета О и положительное направление дуговой координаты s вдоль траектории.
При решении «прямой» задачи кинематики по известному закону движения путем дифференцирования находятся кинематические характеристики: скорость, ускорение и др.
При решении «обратной » задачи по заданному ускорению путем интегрирования можно найти скорость и положение точки в момент времени t, при этом необходимо дополнительно знать начальные условия, т.е. скорость и положение точки в момент времени t = 0.
При решении задач на относительную скорость целесообразно использовать закон сложения скоростей, записанный в векторной форме. При этом важно понимать, как движется подвижная система координат относительно неподвижной.
В кинематике твердого тела можно выделить пять видов движения твердого тела: а) поступательное; б) вращение вокруг неподвижной оси; в) плоское; г) движение вокруг неподвижной точки; д) свободное. При этом основными видами являются поступательное и вращательное движение вокруг неподвижной оси. Более сложные движения можно рассматривать как совокупность основных.
При поступательном движении твердого тела все точки за одинаковые промежутки времени совершают одинаковые переме-щения, поэтому задачу можно свести к кинематике поступательного движения точки.
Кинематическими характеристиками вращательного движения твердого тела вокруг неподвижной оси являются угол поворота, угловая скорость, угловое ускорение. Следует помнить, что это аксиальные векторы. Векторы угла поворота и угловой скорости совпадают и связаны с направлением поворота правилом правого винта. Вектор углового ускорения сонаправлен с угловой скоростью в случае ускоренного движения и направлен противо-положно при замедленном движении.
В ряде задач необходимо знать и использовать связь между линейными и угловыми кинематическими величинами 1.16-1.19 и 1.20-1.23.
Примеры решения задач
Задача 1.1.
Тело брошено вертикально вверх с
начальной скоростью
![]() м/с. Определить максимальную высоту его
подъема над землей
м/с. Определить максимальную высоту его
подъема над землей
![]() и длину пути
,
пройденного им за
и длину пути
,
пройденного им за
![]() с от начала движения. На какой высоте
находится тело в конце третьей секунды?
с от начала движения. На какой высоте
находится тело в конце третьей секунды?
Движение прямолинейное:
при подъеме – равнозамедленное с
ускорением
![]() и начальной скоростью
и начальной скоростью
![]() ,
при спуске – равно-ускоренное с начальной
скоростью
,
при спуске – равно-ускоренное с начальной
скоростью
![]() .
.
Длина пути
складывается из максимальной высоты
подъёма
![]() и пути
и пути
![]() ,
которое тело прошло на спуске от верхней
точки траектории.
,
которое тело прошло на спуске от верхней
точки траектории.
Время подъема
![]() определяется условием
определяется условием
![]()
![]() (с);
(с);
![]() м,
м,
![]()
где
![]() отсчитывается от начала спуска:
отсчитывается от начала спуска:
![]() с,
тогда искомый путь
с,
тогда искомый путь
![]() м.
м.
Высота подъема в данной задаче совпадает с вектором перемещения за 3 с движения:
![]() м.
м.
Задача 1.2.
Зависимость пути от времени задана как
![]() .
Определить скорость тела, ускорение
.
Определить скорость тела, ускорение
![]() к концу второй секунды движения.
к концу второй секунды движения.
По определению,
![]() (м/с),
(м/с),
![]() (м/с2).
(м/с2).
Задача 1.3.
Путь задан функцией времени
![]() Найти среднюю скорость движения между
Найти среднюю скорость движения между
![]() с и
с и
![]() с. Какова средняя скорость на первых
восьми метрах пути тела?
с. Какова средняя скорость на первых
восьми метрах пути тела?
По определению,
![]() где
где
![]()
![]()
![]() с.
с.
Подставляя числовые
значения, получаем
![]() м/с; а модуль мгновенной скорости
определяется функцией
м/с; а модуль мгновенной скорости
определяется функцией
![]()
Первые восемь метров
пути
![]() тело проходит за
тело проходит за
![]() ,
тогда
,
тогда
![]() м/с.
м/с.
Задача 1.4. Материальная точка движется в плоскости XY по закону x = 3+2t, y = 2t - 4t2. Найти уравнение траектории движения и радиус кривизны траектории в начальный момент времени.
Уравнение траектории y = f(x) получаем, исключая t из системы уравнений
![]() ,
,
полученное уравнение
![]() соответствует параболе, ветви которой
направлены вниз.
соответствует параболе, ветви которой
направлены вниз.
Радиус кривизны
находим из (1.23)
![]() где
где
![]()
![]()
Далее
![]()
![]()
![]()
![]()
Тогда
![]() а при t = 0
а при t = 0
![]() Полное ускорение
Полное ускорение
![]() ,
,
с другой стороны
![]() где
где
![]()
В начальный момент времени
![]()
Итак, искомый радиус
кривизны в начальный момент времени
![]() (м).
(м).
Задача 1.5.
Тело брошено с поверхности Земли с
начальной скоростью
![]() м/с
под углом
м/с
под углом
![]() к горизонту. Определить, на каком
расстоянии от точки бросания находится
тело спустя время
к горизонту. Определить, на каком
расстоянии от точки бросания находится
тело спустя время
![]() от начала движения; какой угол составляет
вектор скорости с горизонтом и величины
нормальной и тангенциальной составляющих
ускорения в этот момент времени.
от начала движения; какой угол составляет
вектор скорости с горизонтом и величины
нормальной и тангенциальной составляющих
ускорения в этот момент времени.
Движение тела
происходит по параболе, ускорение
постоянно и равно ускорению свободного
падения
![]() .
Пусть тело в момент времени
.
Пусть тело в момент времени
![]() с
находится в точке А
(рис. 1.3). Запишем основные уравнения
(1.9) и (1.11) для вектора
с
находится в точке А
(рис. 1.3). Запишем основные уравнения
(1.9) и (1.11) для вектора
![]() и скорости
:
и скорости
:
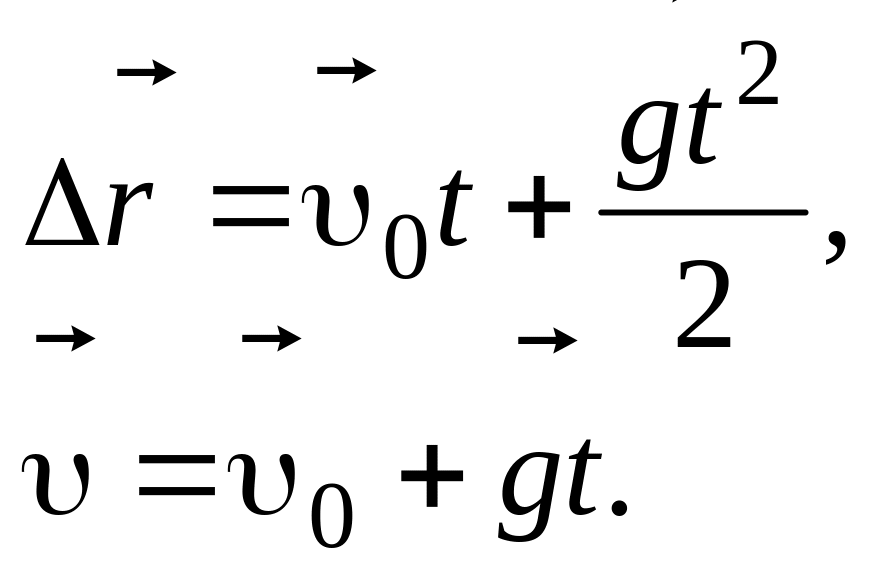
Спроецируем эти
уравнения на оси
![]() и
и
![]() :
:
![]()
 (1.24)
(1.24)
где
![]() – координаты точки А,
в которой находится тело в момент времени
– координаты точки А,
в которой находится тело в момент времени
![]() с.
Используя уравнения (1.24), находим искомое
расстояние
с.
Используя уравнения (1.24), находим искомое
расстояние
 м.
м.

При
решении задач на определение составляющих
ускорения
![]() (тангенциальной и нормальной) или радиуса
кривизны траектории R
проще всего использовать тот факт, что
вектор скорости
всегда направлен по касательной к
траектории и угол
(тангенциальной и нормальной) или радиуса
кривизны траектории R
проще всего использовать тот факт, что
вектор скорости
всегда направлен по касательной к
траектории и угол
![]() между вектором
и осью Х
как функция времени
определяется
условием
между вектором
и осью Х
как функция времени
определяется
условием
![]() . (1.25)
. (1.25)
Угол между вектором полного ускорения и его нормальной компонентой также равен , т.е. для компоненты ускорения согласно рис. 1.4:
![]()
![]() . (1.26)
. (1.26)
Используя (1.25) находим, что через 1 с после начала движения:
![]() т.е.
т.е.
![]()

Далее, согласно (1.26):
![]() м/с2
,
м/с2
,
![]() .
.
Для данных начальных условий тело через 1 с находится в верхней точке траектории.
Задача 1.6.
Тело брошено с вышки, высота которой
![]() м, со скоростью
м, со скоростью
![]() м/с под углом
к горизонту. Найти радиус кривизны
траектории как функцию времени. Вычислить
радиус кривизны через 4 с после начала
движения? Какова максимальная высота,
которой достигнет тело и какова дальность
его полета? Сопротивлением воздуха
пренебречь.
м/с под углом
к горизонту. Найти радиус кривизны
траектории как функцию времени. Вычислить
радиус кривизны через 4 с после начала
движения? Какова максимальная высота,
которой достигнет тело и какова дальность
его полета? Сопротивлением воздуха
пренебречь.
Проекции скорости
на выбранные (рис. 1.5) оси координат
![]()
![]() .
Время подъема
определяется условием
.
Время подъема
определяется условием
![]() в верхней точке траектории:
в верхней точке траектории:
![]() ,
отсюда
,
отсюда
![]() с.
с.

Рис. 1.5
Высота подъема над
уровнем
![]() определяется из уравнения для координаты
y
системы (1.24)
определяется из уравнения для координаты
y
системы (1.24)
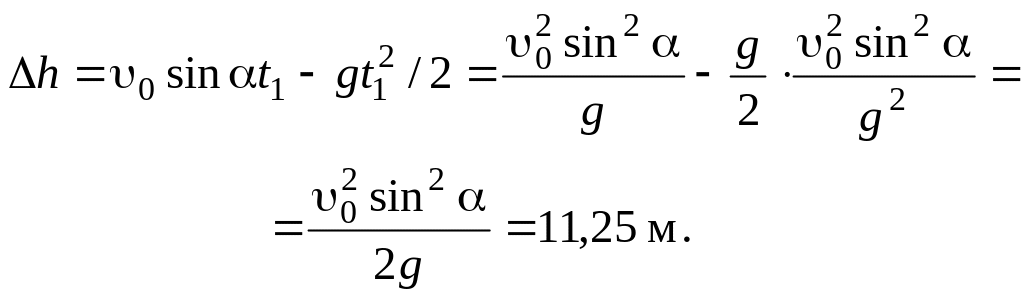
Согласно рис. 1.5
максимальная высота подъема
![]() =61,25 м.
=61,25 м.
Время всего движения
определяется из условия y = 0,
т.е.
![]() .
.
Полученное квадратное
уравнение
![]() имеет два
корня: 5 и -2, тогда время полёта тела
равно 5 с.
имеет два
корня: 5 и -2, тогда время полёта тела
равно 5 с.
Теперь можно вычислить
дальность полёта
![]() м.
м.
Радиус кривизны
может быть определен из
где
из (1.26)
![]() Тогда
Тогда
![]()
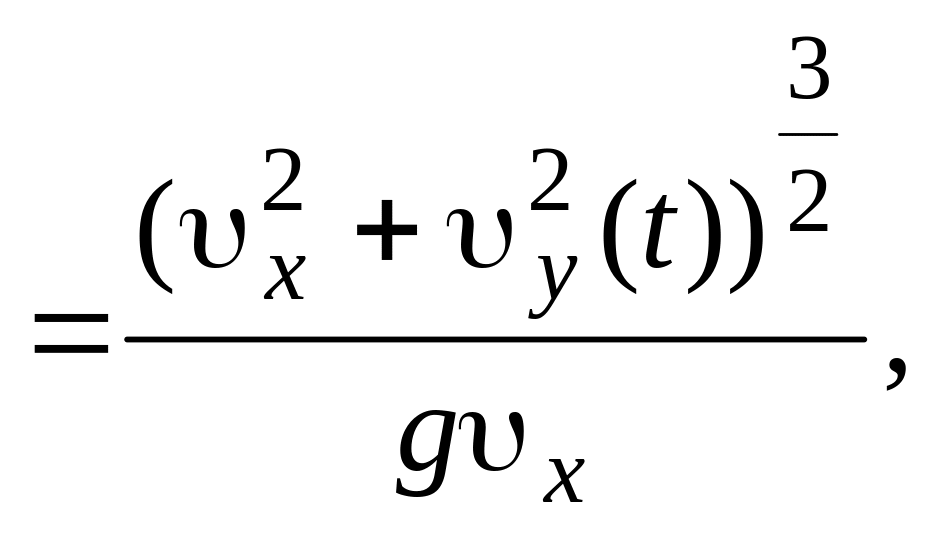 в момент времени
= 4 с получаем
в момент времени
= 4 с получаем
![]() м.
м.
Задача 1.7.
Тело, брошенное под углом
![]() к горизонту, спус-тя время
имело нормальное ускорение
к горизонту, спус-тя время
имело нормальное ускорение
![]() а через
время
а через
время
![]() упало на Землю. Под каким углом было
брошено тело?
упало на Землю. Под каким углом было
брошено тело?
Зная значение нормального ускорения в момент времени , из (1.26) находим угол (рис. 1.6):
![]()
или
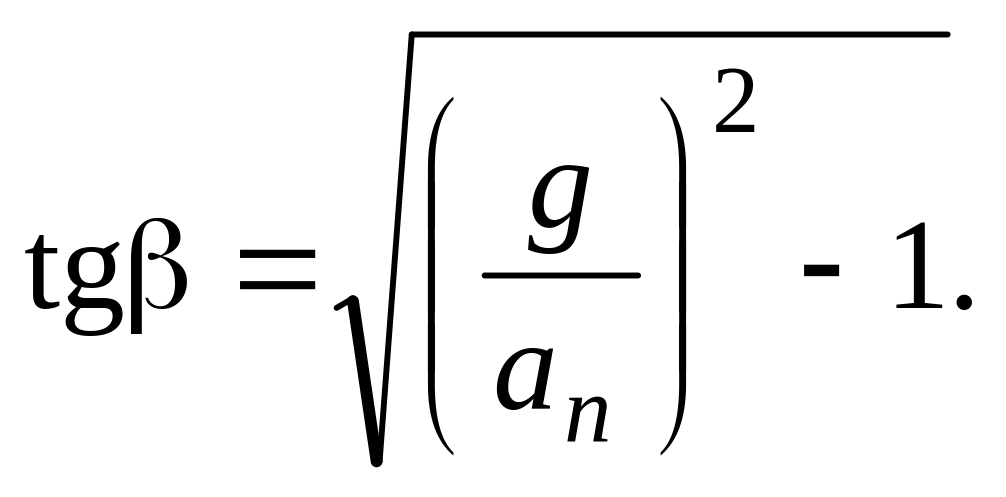
Рис.
1.6
С другой стороны, согласно (1.25),
![]()
Согласно условию
задачи полное время движения
![]() ,
откуда
,
откуда
![]()
Тогда
![]() а
а
![]() .
.
Искомый угол
определяется выражением
![]()
Задача
1.8.
Из одного пункта в одинаковом направлении
выходят два тела с начальными скоростями
![]() м/с и
м/с и
![]() м/с. Второе выходит на
м/с. Второе выходит на
![]() с позже первого. С каким предельным
(одинаковым у обоих и постоянным во
времени) ускорением они могут двигаться,
чтобы второе тело смогло догнать первое?
с позже первого. С каким предельным
(одинаковым у обоих и постоянным во
времени) ускорением они могут двигаться,
чтобы второе тело смогло догнать первое?
Второе тело сможет догнать первое, если к моменту выхода второго скорость первого не будет превышать начальной скорости второго, так как они движутся с одинаковыми ускорениями, т.е.
![]() и
и
![]()
![]() м/с2.
м/с2.
Задача 1.9.
Тело вращается относительно неподвижной
оси с постоянным угловым ускорением
![]() рад/с2.
Определить
,
,
рад/с2.
Определить
,
,
![]() точек тела, находящихся на расстояниях
R=2
м от оси вращения. Найти угловую и
линейную скорости этих точек через 3 с
от начала вращения. Сколько оборотов
совершило тело за это
время?
точек тела, находящихся на расстояниях
R=2
м от оси вращения. Найти угловую и
линейную скорости этих точек через 3 с
от начала вращения. Сколько оборотов
совершило тело за это
время?
Угловая скорость
для любой точки тела одинакова и равна:
![]() рад/с. Линейная скорость зависит от
расстояния точки до оси вращения:
рад/с. Линейная скорость зависит от
расстояния точки до оси вращения:
![]() (м/с).
(м/с).
Нормальная и тангенциальная составляющие ускорения согласно (1.23) и (1.22) соответственно равны:
![]() (м/с2)
и
(м/с2)
и
![]() (м/с2).
(м/с2).
Найдём полное
ускорение
![]() (м/с2).
(м/с2).
Угол, на который
повернётся тело за 3 с, определяется
согласно (1.14):
![]() (рад),
тогда число оборотов тела
(рад),
тогда число оборотов тела
![]() .
.
Задача 1.10.
Колесо вращается вокруг неподвижной
оси (рис. 1.7) так, что угол
![]() его поворота зависит от времени, как
его поворота зависит от времени, как
![]() где
где
![]() рад/с2.
Найти полное ускорение точки А
на ободе колеса в момент
рад/с2.
Найти полное ускорение точки А
на ободе колеса в момент
![]() с, если линейная скорость точки А
в этот момент
с, если линейная скорость точки А
в этот момент
![]() м/с.
м/с.

Рис. 1.7
Модуль полного
ускорения точки А
определяется значениями тангенциального
и нормального ускорений в соответствии
с выражением
![]() .
.
Определяем тангенциальное ускорение (1.22):
![]() .
.
Нормальное
ускорение связано с угловой скоростью
и радиусом окружности
соотношением (1.23):
![]() где
где
![]()
Радиус окружности находим, используя связь между линейной и угловой скоростями (1.21):
![]()
Тогда
![]() м/с2.
м/с2.
Задача 1.11.
Шарик радиусом
![]() см может вращаться относительно
горизонтального стержня 00,
который, в свою очередь, вращается
относительно вертикальной оси, при этом
шарик катится по горизонтальной
поверхности без проскальзывания.
Расстояние от вертикальной оси до центра
шара
см может вращаться относительно
горизонтального стержня 00,
который, в свою очередь, вращается
относительно вертикальной оси, при этом
шарик катится по горизонтальной
поверхности без проскальзывания.
Расстояние от вертикальной оси до центра
шара
![]() см.
Линейная скорость центра масс шарика
см.
Линейная скорость центра масс шарика
![]() см/с.
Определить вектор угловой скорости
шарика.
см/с.
Определить вектор угловой скорости
шарика.
Шарик имеет две
степени свободы: вращение относительно
вертикальной оси с угловой скоростью
![]() и относительно горизонтальной оси –
и относительно горизонтальной оси –
![]() .
Тогда как видно на рис. 1.8 вектор
угловой скорости в этом движении
определяется
.
Тогда как видно на рис. 1.8 вектор
угловой скорости в этом движении
определяется
![]() .
.
Линейная скорость
центра шарика
![]() связана с
соотношением
связана с
соотношением
![]() ,
откуда
,
откуда
![]() .
За один оборот относительно вертикальной
оси шарик повернется относительно
горизонтальной оси
.
За один оборот относительно вертикальной
оси шарик повернется относительно
горизонтальной оси
![]() раз.
раз.

Рис. 1.8
Так как проскальзывания нет, число оборотов равно
![]()
Отсюда частота
вращения шарика относительно горизонтальной
оси
![]() ,
а
,
а
![]() .
.
Модуль вектора
угловой скорости
![]() равен:
равен:
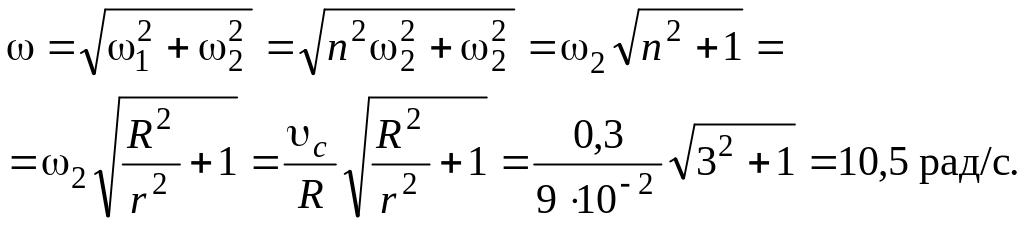
Угол между вектором угловой скорости и горизонтальной плоскостью определяется соотношением
![]()
Задача 1.12.
В момент времени
![]() частица начала двигаться из начала
координат в положительном направлении
оси
(рис. 1.9). Ее скорость меняется со
временем по закону
частица начала двигаться из начала
координат в положительном направлении
оси
(рис. 1.9). Ее скорость меняется со
временем по закону
![]() где
– вектор начальной скорости, модуль
которого
где
– вектор начальной скорости, модуль
которого
![]() м/с,
м/с,
![]() с2.
Найти путь
с2.
Найти путь
![]() ,
пройденный частицей за время
,
пройденный частицей за время
![]() с.
с.
Рис. 1.9
Найдем выражение
для вектора
![]() ,
используя известную зависимость скорости
от времени (1.9):
,
используя известную зависимость скорости
от времени (1.9):
![]()
Модуль вектора
перемещения за полное время движения
![]() .
.
Путь
,
пройденный точкой за 5 с складывается
из пути частицы до остановки в точке А
и пути в обратном направлении до точки
В.
Из рисунка очевидно, что искомый путь
можно вычислить как
![]() где
– время, прошедшее от начала движения
до поворота в точке А.
Время
определяем из условия
где
– время, прошедшее от начала движения
до поворота в точке А.
Время
определяем из условия
![]() откуда
откуда
![]() ,
или
,
или
![]() с. Подставив
и
в выражение для
с. Подставив
и
в выражение для
![]() получим
получим
![]() м.
м.
Задача 1.13. Точка движется, замедляясь по окружности радиусом , так, что ее тангенциальное ускорение все время равно нормальному. Найти закон изменения величины скорости, полагая, что в начальный момент времени точка имела скорость . Определить зависимость пройденного пути от времени.
Запишем условие равенства тангенциального (1.7) и нормального (1.6) ускорений в виде
![]() .
.
Знак “минус”
соответствует замедленному движению
![]() Перепишем это равенство в виде
Перепишем это равенство в виде
![]()
Интегрируя по времени от 0 до , получаем с учетом начальных условий
![]()
откуда выражаем
как функцию времени
:
![]()
Зависимость пройденного телом пути от времени находим, используя (1.8):
![]()
