2.2. Задания на самостоятельную работу

• Исследовать на экстремум функции:

1) y = 2 + x – x²; 2) y = 2x² – x⁴; 3) y = – x; 4) y = x∙e^–x.

• Найти полные дифференциалы функций:

1) u =  sin²y; 2) u = e^x/y; 3) u = ; 4) u = 2x

• Решить задачи:

1) Реакция организма R на введение некоторой дозы лекарственного вещества в зависимости от времени t, отсчитываемого от момента введения, описывается выражением: R₁(t) = ate^–t, где а  1 – постоянный коэффициент. Реакция организма на введение другого лекарства в той же дозе определяется: R₂(t) = at²e^–t. На действие какого из лекарств максимальная реакция организма выше? Какое из лекарств действует медленнее?

2) На сколько изменится объем цилиндра с радиусом основания 2 м и высотой 1 м, если радиус уменьшится на 2 см, а высота увеличится на 3 см?

3) На сколько процентов изменится мощность, выделяемая в проводнике, если его сопротивление увеличится на 2 %, сила тока уменьшится на 3 %?

Занятие №3. Основы интегрального исчисления

3.1. Основные свойства интегралов

1) ;

2) , где С = const;

3) , где а = const;

4) ∫ [v (x) + u(x)] dx = ∫ v (x)dx + ∫ u (x)dx;

5) – формула Ньютона-Лейбница;

6) ;

7) .

3.2. Таблица некоторых основных интегралов

( x ≠ – 1)

3.3. Примеры нахождения интегралов непосредственным интегрированием

1) ;

2) ;

3) ;

4) .

3.4. Примеры нахождения интегралов методом замены переменной

1) ;

2) ;

3) .

3.5. Примеры вычисления определенных интегралов

1)

2)

3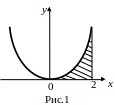 .6. Примеры вычисления площадей фигур, ограниченных линиями

1) Найти площадь фигуры, ограниченной линиями y_{1 ­­}= 2 x², y_{2 ­­}= 0, x = 0, x = 2

Решение. На рисунке 1 искомая площадь S заштрихована

2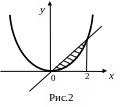 ) Найти площадь фигуры, ограниченной линиями y_{1 ­­}= x², y_{2 ­­}= x.

Решение. На рисунке 2 искомая площадь S заштрихована. Пределы интегрирования определяются из условия x² = х; х (х – 1) = 0. Таким образом, нижний предел x₁ = 0, а верхний предел x₂ = 1. Искомая площадь определяется интегрированием:

.

3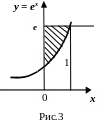 ) Найти площадь фигуры, ограниченной линиями y_{1 ­­}= e^x, y_{2 ­­}= e, x = 0.

Решение. На рисунке 3 искомая площадь S заштрихована. Из рисунка видно, что нижний предел интегрирования x₁ = 0. а верхний x₂ = 1 ( из условия e^x = е). Таким образом, искомая площадь определяется интегрированием:

3.7. Задания на самостоятельную работу

• Найти интегралы:

1. ; 2. ; 3. ;

4. ; 5. ; 6. .

• Вычислить определенные интегралы:

1. ; 2. ; 3. ;

4. ; 5. ; 6. .

• Вычислить площади фигур, ограниченных линиями:

1. у = 4 –х², у = 0; 2. у = х² – 2, у = 6 – х²; 3. у = х³, х = 2, х =3.

Занятия №4 и №5. Дифференциальные уравнения

1. Основные определения

Дифференциальным называют уравнение, связывающее аргумент х, искомую функцию у и ее производные у’,у”, ...,у⁽ⁿ⁾ различных порядков. В общем виде дифференциальное уравнение можно записать:

F (x, y, у’,у”, ...,у⁽ⁿ⁾) = 0.

Порядок дифференциального уравнения определяется наивысшим порядком входящей в него производной.

Решением дифференциального уравнения является такая функция, которая обращает это уравнение в тождество.

Общее решение дифференциального уравнения содержит столько производных постоянных, каков порядок дифференциального уравнения.

Если наряду с исходным дифференциальным уравнением заданы некоторые добавочные сведения (начальные условия), то они позволяют определить произвольные постоянные, входящие в общее решение и получить частное решение дифференциального уравнения, которое не содержит произвольных постоянных.