
- •Занятие №1 Основы дифференциального исчисления. Производная функции
- •1.1. Таблица некоторых производных элементарных функций.
- •1.2. Правила дифференцирования
- •1.3. Примеры нахождения производных
- •1.4. Найти производные функций
- •1 .5. Решить задачи
- •Занятие №2. Экстремумы функций. Дифференциал функции. Частные производные и полный дифференциал
- •2.1. Примеры и задачи с решениями.
- •2.2. Задания на самостоятельную работу
- •3.7. Задания на самостоятельную работу
- •Занятия №4 и №5. Дифференциальные уравнения
- •Основные определения
- •Примеры решения дифференциальных уравнений методом разделения переменных
- •Примеры решения задач, требующих составления дифференциальных уравнений
- •5.1. Задания на самостоятельную работу
- •Занятие №6. Элементы теории вероятности
- •6.1 Основные определения
- •6.2. Примеры решения задач
- •6.3. Задания на самостоятельную работу
- •Занятие №20. Электропроводимость биологических тканей и жидкостей Лабораторная работа: «Определение зависимости импеданса биологической ткани от частоты тока»
- •20.1. Ток в электролитах
- •20.2. Особенности электропроводимости биологических тканей
- •20.3. Гальванизация и лекарственный электрофорез.
- •20.4. Полное сопротивление (импеданс) цепи переменного тока
- •20.5. Электропроводимость биологических тканей для переменного тока. Импедансные методы в биологических и медицинских исследованиях
- •Порядок выполнения лабораторной работы
- •20.7. Задания на самостоятельную работу
Занятие №1 Основы дифференциального исчисления. Производная функции
1.1. Таблица некоторых производных элементарных функций.
1) (С)
′ = 0; С = const
2)
![]()
3)
![]() 3а)
3а)
![]()
4)
![]() 4а)
4а)
![]()
5)
![]() 6)
6)
![]()
7)
![]() 8)
8)
![]()
1.2. Правила дифференцирования
Пусть u( x ) и v( x ) – произвольные функции аргумента x. Тогда:
1)![]()
![]()
2)
![]()
3)
![]()
![]()
5) Производная сложной функции y = f (u), где u = f(x) :
![]()
1.3. Примеры нахождения производных
1)
![]() ;
;
2)
![]() ;
;
3)
![]() ;
;
4)
![]() ;
;
5)
![]() .
.
6) Зависимость пути S (в метрах), проходимого телом, от времени t (в секундах) определяется законом S = 2 + t3– 3t2 + 2t. Найти скорость v и ускорение а через 2 секунды после начала движения тела.
Решение. Скорость тела представляет собой производную от пути по времени: v = (S)′ = (2 + t 3– 3t2 + 2t)′ = 3 t2 – 6 t + 2. Через 2 секунды v (t = 2) = 2 м/с.
Ускорение – это «скорость изменения скорости движения», т.е. ускорение определяется первой производной от скорости или второй производной от пути по времени: a (t) = v (t)′ = S (t) ″ = 6 t – 6.
Через 2 секунды a (t = 2) = 6 м/с2.
7) Атмосферное давление P с увеличением высоты h над поверхностью Земли изменяется по закону: P = P0 e–kh, где P0 – давление на поверхности Земли, k - коэффициент, который можно считать постоянным для данной температуры. Определить градиент давления.
Решение. Упрощенно, градиент некоторой величины, зависящей от расстояния, представляет собой производную от этой величины по пространственной координате h:
grad P = (P)′h = – kP0 e–kh..
Знак «минус» в полученном результате указывает на то, что давление убывает с увеличением высоты над поверхностью Земли.
1.4. Найти производные функций
1. у
= 2 а х3; 2.![]() ;
3. у = sin2 3 x;
;
3. у = sin2 3 x;
4. у = х3 ∙ ln x;
5.
![]() ;
6.
;
6.
![]() ;
;
7. ![]() ;
8. у = (sin2 x
+ 8 x)9.
;
8. у = (sin2 x
+ 8 x)9.
1 .5. Решить задачи
1. График функции имеет вид трапеции (см. рисунок). Построить график производной этой функции.
2. Количество электричества Q (в кулонах), протекшего через проводник за время t (в секундах) определяется формулой: Q = 2t2 + 3t + 1. Найти силу тока в конце пятой секунды.
3. Смещение l мышечного волокна в ответ на одиночный электрический импульс зависит от времени t по закону: l = tе – t. Найти зависимость скорости смещения волокна от времени.
4.
Концентрация С некоторого вещества
убывает с увеличением толщины х слоя
биоткани по закону:
![]() ,
где С0 – концентрация
на поверхности слоя, к – постоянная.
Определить градиент концентрации.
,
где С0 – концентрация
на поверхности слоя, к – постоянная.
Определить градиент концентрации.
Занятие №2. Экстремумы функций. Дифференциал функции. Частные производные и полный дифференциал
2.1. Примеры и задачи с решениями.
1)
Исследовать на экстремум функцию
![]() .
.
Решение.
Находим производную заданной функции:
![]()
Так как в точке максимума или минимума функции ее производная равна нулю, находим корни уравнения х2 – х = 0. х (х – 1) = 0
 х1 = 0, х2
= 1.
х1 = 0, х2
= 1.Чтобы определить, где функция имеет максимум, а где минимум, находим вторую производную заданной функции:
у″ = (х2 – х) ′ = 2х – 1.
При х1 = 0 у″ (х1 = 0) = –1 < 0. Значит, в точке х = х1 = 0 функция имеет максимум.
При х2 = 1 у″ (х2 = 1) = 1 > 0. Значит, в точке х = х2 = 1 функция имеет минимум.
График функции имеет вид:
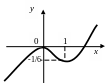
2) Путь S (в метрах), проходимый движущимся телом, зависит от времени (в секундах) по закону: S = 5 – 13t + 12t2 – t3. Определить максимальную скорость тела.
Решение: По заданной зависимости пути от времени установим как скорость движения (производная от пути по времени) зависит от времени:
v (t) = S ′ = (5 – 13t + 12t2 – t3)′ = –13 + 24 t – 3 t2.
Для получения ответа на поставленный в условии вопрос необходимо исследовать на экстремум функцию v (t). Для этого находим производную от скорости и приравниваем ее нулю:
v ′ = (– 13 + 24 t – 3 t2 ) ′ = 24 – 6 t = 0 t = 4.
Следовательно, скорость движения экстремальна в момент времени t = 4с. Так как вторая производная от скорости отрицательна (v" = –6) , то через 4 с после начала движения скорость достигает максимального значения vmax = 35 м/с.
3) Найти дифференциал функции y = x ∙sin 2x + x2.
Решение. Дифференциал функции – это произведение производной функции на приращение (дифференциал) аргумента: dy = y' dx. Для заданной в условии функции:
dy =d ( x ∙sin 2x + x2) = ( x ∙sin 2x + x2)′∙dx = (sin 2x + 2 x cos 2x +2x) dx.
4) Количество энергии R, теряемое телом человека при испускании им инфракрасных лучей, пропорционально четвертой степени температуры Т:
R = aT 4 , где а – постоянная. На сколько процентов увеличилось количество энергии R, если температура тела увеличилась на 2 %?
Решение. При небольшом изменении аргумента (температуры Т) приращение функции (количества энергии R) можно считать примерно равным ее дифференциалу:
∆ R ≈ d R = ( aT 4)′ dT = 4 aT 3 dT .
Разделив левую и правую части полученного равенства на R = aT 4, получим:
![]() .
.
Значит,
если относительно изменение температуры
![]() ,
то изменение количества излучаемой
энергии
,
то изменение количества излучаемой
энергии
![]() .
.
5) Найти частные производные функции двух переменных u = y3 sin2 x + 2 y.
Решение.
![]() ;
;
![]() .
.
6) Найти полный дифференциал функции u = x2 e–x 2y + y2 sin x.
Решение.
![]() =
=
![]() .
.
7) Тело массой m = 1 кг движется со скоростью v = 1 м/с. На сколько джоулей изменится кинетическая энергия тела, если его массу уменьшить на 20 г, а скорость увеличить на 4 см/с?
Решение.
Кинетическая энергия
![]() является
функцией двух переменных. При малых
изменениях массы (∆m
= – 0,02 кг) и скорости
(∆v
= 0,04 м/с) изменение кинетической энергии
примерно равно ее полному дифференциалу:
является
функцией двух переменных. При малых
изменениях массы (∆m
= – 0,02 кг) и скорости
(∆v
= 0,04 м/с) изменение кинетической энергии
примерно равно ее полному дифференциалу:
![]()
8)
Реакция R (x,t)
на x
единиц лекарства спустя t
часов после его приема описывается
зависимостью:
![]() ,
где а – постоянный коэффициент для
данного лекарства и данного пациента.
,
где а – постоянный коэффициент для
данного лекарства и данного пациента.
При каком значении дозы x реакция окажется максимальной? Когда наступит максимальная реакция?
Решение. Математически, задача
сводится к нахождению экстремумов
функции R![]() .
Для нахождения максимальной дозы
(максимума по x) необходимо найти
частную производную
.
Для нахождения максимальной дозы
(максимума по x) необходимо найти
частную производную
![]() ,
приравнять ее к нулю и решить полученное
уравнение относительно х:
,
приравнять ее к нулю и решить полученное
уравнение относительно х:
![]()
Это уравнение имеет два корня : х1
=0 и х2 =![]()
Первый из них соответствует минимуму реакции организма (если доза равна нулю – ничего не вводили), а второй – максимуму. В справедливости этого утверждения легко убедиться и чисто математически, используя правила исследования функций на экстремум.
Таким образом, доза лекарства,
обеспечивающая максимальную реакцию:
х =
![]() .
.
Для нахождения времени наступления
этой максимальной реакции найдем частную
производную
![]() и опять же решим соответствующее
уравнение относительно t:
и опять же решим соответствующее
уравнение относительно t:
![]() =
(2x - 3х2) 2 t
e-t
- (2ax-
3x2) t2
e-t
= 0.
=
(2x - 3х2) 2 t
e-t
- (2ax-
3x2) t2
e-t
= 0.
Это уравнение имеет корни t1= 0, t2 = 2. По смыслу задачи и из математического анализа, следует, что первый корень (t1 = 0) соответствует минимуму реакции, а второй – максимуму. Если, например, в уравнении время определялось в часах, то максимальная реакция наступит через 2 часа.
