Примеры решения задач.

1. Сплошной однородный диск радиуса R = 10см, имевший начальную угловую скорость ω₀ = 50рад/с (относительно оси, перпендикулярной плоскости диска и проходящей через центр масс), кладут основанием на горизонтальную поверхность. Сколько оборотов сделает диск до остановки, если коэффициент трения между основанием диска и горизонтальной поверхностью μ = 0,1 и не зависит от угловой скорости вращения диска.

Р ешение.

Физическая система состоит из одного тела – диска. Диск нельзя считать материальной точкой. Примем его за твёрдое тело. Физическое явление заключается во вращательном движении твёрдого тела относительно неподвижной оси под действием силы трения (остальные силы взаимно уравновешивают друг друга). Начальное и конечное состояние системы известны. Необходимо определить один из параметров этого движения (число оборотов N до остановки). Это основная задача динамики твёрдого тела.

Применим динамический метод. Центр масс диска находится в покое, а диск вращается. Из уравнения движения получаем

,

г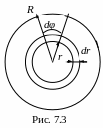 де m = πR²hρ – масса диска.

Сила трения приложена к каждому участку диска, и так как эти участки находятся на различных расстояниях от оси, то и моменты сил трения, приложенных к этим участкам, различны. Для нахождения М применим метод ДИ (дифференцирования и интегрирования). Разделим диск на достаточно узкие кольца (рис. 7.3), а каждое кольцо двумя соседними радиусами, образующими достаточно малый угол dφ, – на малые элементы. На рисунке один такой элемент заштрихован. Сила трения, действующая на выделенный элемент,

dF_mp = μdφrdrhρg

Момент этой силы трения

dM = rdF_mp = μdφr²drhρg

Интегрируя по углу φ в пределах от нуля до 2π и по r от нуля до R, получаем суммарный момент сил трения:

Подставляя это значение суммарного момента сил в уравнение движения, находим угловое ускорение диска:

Решая далее обратную задачу кинематики (кинематический метод), определяем закон изменения угловой скорости

ω = ω₀ – εt

и закон движения:

Учитывая, что конечная угловая скорость равна нулю, находим время движения:

с

Подставляя это значение в закон движения и учитывая, что φ = 2πN, получаем

Решим теперь эту задачу методом законов сохранения. В физическую систему включим два тела: диск и Землю. Система этих тел замкнута и можно было бы применять закон сохранения энергии в механике, но в системе действуют неконсервативные силы трения. Считая эти силы внешними, находим:

,

где - момент инерции диска, А – работа неконсервативных сил трения. Т.к. момент этих сил уже найден, то получаем:

Подставляя это выражение работы в предыдущую формулу, и учитывая, что φ = 2πN, получаем

,

что совпадает с формулой, найденной динамическим методом.

Ответ: N ≈ 15.

2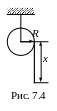 . Однородный сплошной цилиндр массы m₀ и радиуса R может без трения вращаться вокруг неподвижной оси О (рис. 7.4). На цилиндр в один ряд намотан тонкий нерастяжимый шнур длины l и массы m. Найти угловое ускорение цилиндра в зависимости от длины х свешивающейся части шнура. Считать, что скольжения нет и центр масс намотанной части шнура находится на оси цилиндра.

Р ешение.

Воспользуемся уравнением моментов относительно оси О. Для этого найдём момент импульса системы относительно данной оси, L_z, и соответствующий момент сил M_z. Момент импульса

,

где учтено, что момент инерции цилиндра и υ = ω_zR (отсутствие скольжения шнура). Момент внешних сил тяжести относительно оси О

.

Продифференцировав L_z по времени и подставив и M_z в уравнение моментов, получим:

.

Ответ: .

3. На гладкой горизонтальной плоскости лежит однородный диск радиуса r₀. На него осторожно опустили другой такой же диск, предварительно сообщив ему угловую скорость ω₀. Через сколько времени оба диска будут вращаться с одной и той же угловой скоростью, если коэффициент трения между дисками равен μ?

Р ешение.

Сначала найдём установившуюся угловую скорость вращения ω. Из закона сохранения момента импульса следует, что

Jω₀ = 2 Jω,

где J- момент инерции каждого диска относительно общей оси вращения. Отсюда

.

Теперь рассмотрим поведение одного из дисков, например, нижнего. Его угловая скорость меняется под действием момента M сил трения. Вычислим M. Для этого выделим на верхней поверхности диска элементарное кольцо с радиусами r, r + Δr. Момент сил трения, действующих на данное кольцо, равен:

,

где m - масса каждого диска. Проинтегрировав это выражение по r от 0 до r₀, получим:

.

Приращение угловой скорости нижнего диска на величину dω за время

Интегрируя это уравнение по ω от 0 до , находим, что искомое время

.

Ответ: .

4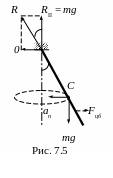 . Тонкий однородный стержень массы m и длины l вращается с постоянной угловой скоростью ω вокруг вертикальной оси, проходящей через его точку подвеса О (рис. 7.5). При этом стержень описывает коническую поверхность с некоторым углом полураствора . Найти угол , а также модуль и направление силы реакции R в точке О.

Р ешение.

Рассмотрим систему отсчёта, вращающуюся вокруг вертикальной оси вместе со стержнем. В этой системе на стержень действует кроме силы тяжести mg и силы реакции R ещё центробежная сила F_цб. Так как стержень покоится в данной системе отсчёта, т.е. находится в состоянии равновесия, то это значит, что результирующий момент всех сил относительно любой точки и результирующая всех сил равны нулю.

Относительно точки О момент создают только сила тяжести и центробежные силы инерции. Из равенства моментов этих сил следует

(1)

Вычислим M_цб. Элементарный момент сил инерции, который действует на элемент стержня dx, находящийся на расстоянии х от точки О, равен:

.

Проинтегрировав это выражение по всей длине стержня, получим:

(2)

Из (1) и (2) следует, что

(3)

Найдём модуль и направление вектора R. В системе отсчёта, в которой стержень вращается с угловой скоростью ω, его центр масс (точка С) движется по горизонтальной окружности. Поэтому из уравнения движения центра масс сразу следует, что вертикальная составляющая вектора R есть R_II = mg, а горизонтальная составляющая определяется уравнением , где a_n - нормальное ускорение центра масс С. Отсюда

(4)

Модуль вектора R есть

,

а его направление – угол между вектором R и вертикалью определяется формулой . Интересно, что , т.е. вектор R не совпадает по направлению со стержнем. В этом легко убедиться, выразив через :

Отсюда видно, что , т.е. . Это и показано на рисунке.

Заметим, что равнодействующая сил инерции F_цб проходит не через точку С, а ниже. Действительно и определяется формулой (4), а результирующий момент M_цб - формулой (2). Из этих формул следует, что плечо вектора F_цб относительно точки О равно (рис. 7.5).

Ответ: ; ; .

5. Имеются два цилиндра: алюминиевый (сплошной) и свинцовый (полый) - одинакового радиуса R = 6см и одинаковой массы m = 0,5кг. Поверхности цилиндров окрашены одинаково. Как, наблюдая поступательные скорости цилиндров у основания наклонной плоскости, можно различить их? За какое время t каждый цилиндр скатится с наклонной плоскости? Высота наклонной плоскости h = 0,5м, угол наклона плоскости α = 30⁰, начальная скорость каждого цилиндра υ₀ = 0.

Р ешение.

При скатывании тела с наклонной плоскости его потенциальная энергия переходит в кинетическую. Т.е.

,

но . Подставляя, выразим поступательную скорость цилиндров в нижней точке наклонной плоскости:

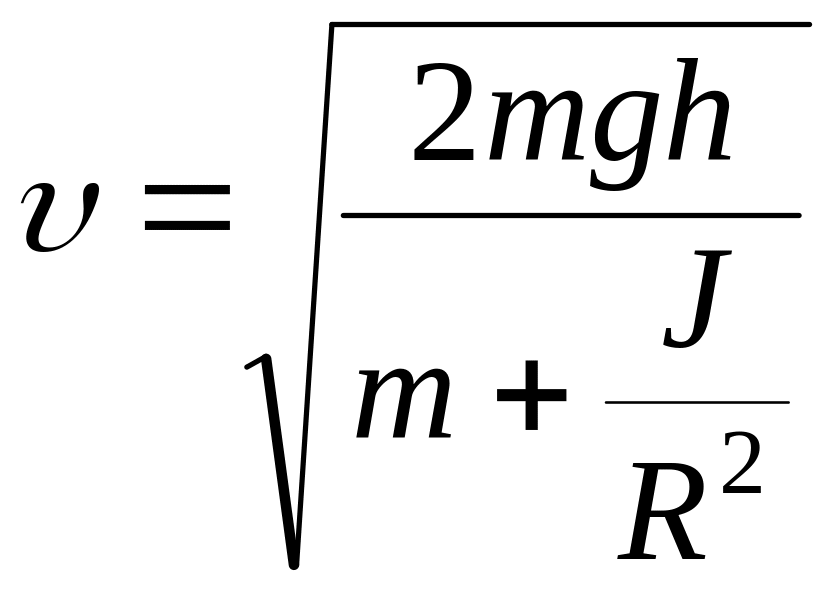(1)

Момент инерции алюминиевого цилиндра – (2). Момент инерции свинцового цилиндра: . Найдём внутренний радиус R₀ свинцового цилиндра. По условию массы обоих цилиндров равны, следовательно,

,

Где ρ₁ и ρ₂ - плотности, соответственно, алюминия и свинца; L – длина цилиндра. Тогда момент инерции свинцового цилиндра

(3)

Подставляя числовые данные, получим: J₁ = 9 ∙ 10⁴ кг^.м² и J₂ = 15,9 ∙ 10⁴ кг^.м². Т.к. скатывание цилиндров происходит под действием постоянной силы, то υ = at и . Отсюда

(4)

Подставляя (4) в (1), получим:

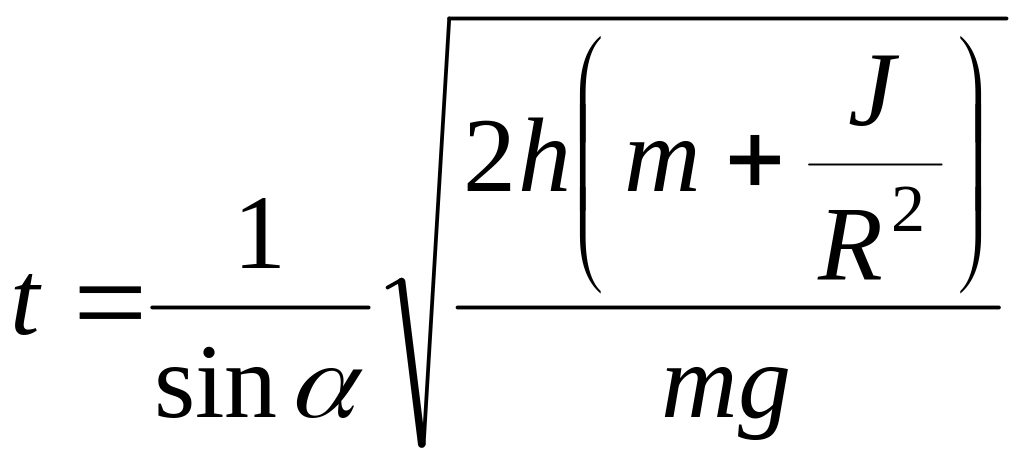(5)

С учётом (2) и (3), получим соответственно для алюминиевого и свинцового цилиндров:

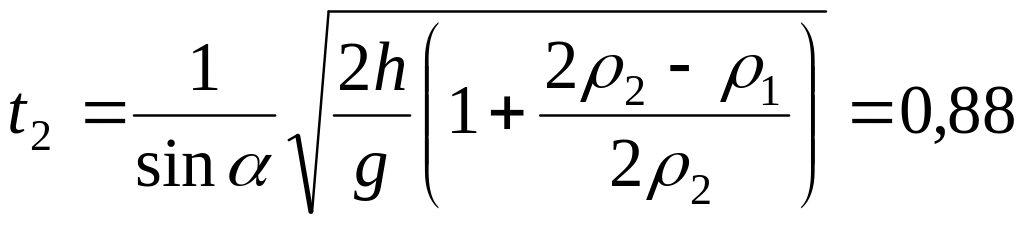с

с

Ответ: t₁ = 0,78с; t₂ = 0,88с.