62. Дайте определение однородной функции нескольких переменных. Приведите пример однородной функции f (X, y) степени 3, не являющейся рациональной функцией.

Пусть D из Rⁿ – область в Rⁿ, содержащая с каждой своей точкой (x₁, x₂, …., x_n) и все точки вида (tx₁, tx₂, …., tx_n) при t>0 функция f(x₁, x₂, …., x_n) с такой областью определения D называется однородной степени λ, если для любого t>0 выполнятся равенство f (tx₁, tx₂, …., tx_n)=t^λ f(x₁, x₂, …., x_n).

Пример однородной функции степени 3:

F (x,y)=x²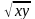

F (tx, ty)=t²x²√(tx*ty)=t³ F (x,y)

63. Докажите, что если однородная степени . функция f (x, y) дифференцируема в точке (x0 , y0 ), то выполнено равенство x0 fx.(x0 , y0 ) + y0 f y.(x0 , y0 ) =. f (x0 , y0 ).

f (tx,ty)=t^λf(x,y)

Продифференцируем левую и правые части этого равенства по t. В результате приходим к тождеству:

F^’_x(tx, ty)x+F^’_y(tx, ty)y=λt^λ-1f(x,y)

Положив здесь t=1,олучим формулу Эйлера:

F^’_x(x, y)x+F^’_y(x, y)y=λf(x,y)

64. Дайте определение локального экстремума функции двух переменных. Является ли равенство нулю частных производных функции в некоторой точке достаточным условием ее локального экстремума в этой точке?

Пусть z=f(x;y) определена в некоторой области D и точка М(х₀;у₀) – внутренняя точка D (М принадлежит D), тогда данная функция в данной точке будет иметь локальный минимум (максимум), если найдется  - окрестность точки М, что для всех внутренних точек этой окрестности, отличных от М(х₀;у₀) выполняются неравенства:

f(x;y)>f(х₀;у₀) – min

f(x;y)<f(х₀;у₀) – max

65. Имеет ли функция f (x, y) = x² y⁴ локальный экстремум в точке (0,0)?

M_o(x_o,y_o) – точка локального min (max)

Для любой M(x,y) из окрестности f(M_o)≤f(M) (f(M_o)≥f(M))

f(x,y)=x 2y4 Mo(0,0)

M(Δx, Δy)

f(Mo)=f(0,0)=0

f(M)= Δx2Δy4

f(M)-f(Mo)= Δx2Δy4-0= Δx2Δy4≥0

f(M) ≥f(Mo) для любого M(x,y) из окрестности Mo

Следовательно, Mo(0,0) – точка локального min

66. Имеет ли функция f (x, y) = x y² локальный экстремум в точке (0,0)?

f(x,y)=xy² M_o(0,0), M(Δx, Δy)

f(0,0)=0, f(M)= ΔxΔy²

f(M)-f(M_o)= ΔxΔy²

f(M)-f(M_o) ≥0 если Δx≥0 ➽ M_o(0,0) не является точкой

f(M)-f(M_o)≤0 если Δx≤0 локального экстремума (по определению)

67. Докажите, что функция f (x, y) = x² + y² : а) не имеет локального экстремума в точке (1, 1), б) имеет в этой точке условный локальный экстремум при наличии связи x + y = 2.

Функция f(x,y)=x²+y²

а) F’_x=2x

F’_y=2y

В точке (1,1) первые производные данной функции не обращаются в ноль, следовательно точка (1,1) не является точкой локального экстремума (не выполняется необходимое условие).

б) Дано уравнение связи x+y=2.

Запишем функцию Лагранжа:

L(x,y)= x²+y²+λ(x+y-2)

L’_x=2x+λ x=y x=1

L’_y=2y+λ ⃗ 2x=2 ⃗ y=1

L’_λ=x+y-2

Следовательно, точка (1,1) является условным экстремумом данной функции при наличии связи.

68. Дайте определение линии уровня функции f (x, y). Рассмотрев множество линий уровня функции f(x, y) = xy, выясните, в каких точках прямоугольника D = {(x, y) | 3  x 6, 4  y 6} она принимает наибольшее и наименьшее значения, и найдите эти значения.

Линией уровня функции z=f(x,y) называется такая линия f(x,y)=c на координатной плоскости, в точках которой функция f(x,y) принимает постоянное значение z=с.

Множество линий уровня функции f(x,y)=xy:

y=c/x – множество гипербол.

D={(x,y)〡3≤x≤6, 4≤y≤6}

f(x,y)=xy

f’ _x=y ⇒ y=0

f’ _y=x x=0

I Найдем стационарные точки внутри области:

(0,0) не является стационарной точкой, т.к. не принадлежит области

II. Найдем стационарные точки на границе области:

а) x=3

z=3y

z’_y=3 – не явл. стационарной точкой

б) x=6

z=6y

z’_y=6 - не явл. стационарной точкой

в) y=4

z’_x=4 - не явл. стационарной точкой

г) y=6

z’_x=6 - не явл. стационарной точкой

III Найдем угловые точки области:

A(3,4), B(6,3), C(6,6), D(4,6)

Z(3,4)=12 – наименьшая точка

Z(6,3)=18

Z(4,6)=24

Z(6,6)=36 – наибольшая

69. Сформул осн св-ва непрерывных ф-ий, заданных на замкнутом ограниченном множестве в R2 . Найдите наибольшее и наим значения функции f (x, y) = x2 + y2 на множестве

D = {(x, y) | (x -5)² + y2 4}.

Свойства непрерывных функций:

1. Если функция u=f(М) определена и непрерывна на замкнутом ограниченном множестве {M} точек Евклидова пространства Rⁿ , то она ограничена на этом множестве, т.е. существует такое с>0, что для любых точек М, принадлежащих {M} выполняется неравенство |f(M)|<c.

2. Если функция u=f(М) непрерывна на замкнутом ограниченном множестве {M}, то она достигает на этом множестве своих верхних и нижних граней множества.

3. Если функция u=f(M) непрерывна на замкнутом ограниченном множестве {M}, то она принимает все промежуточные значения между своими min и max значениями.

4. Результатом алгебраических операций непрерывных функций являются непрерывные функции.

f(x,y)=x²+y²

а) D={(x,y)〡(x-5)²+y²≤4} – круг с центром в (5,0) и радиусом 2 – компакт

б) f’_x=2x x=0 ⇒ не принадлежит области

f’_y=2y y=0

в) (x-5)²+y²=4

y²=4-(x-5)²

z=x²+4-( x²-10x+25)

z= x²+4- x²+10x-25

z=10x-21

z’=10 – не имеет стационарных точек на границе