32. Следует ли из существования производной функции в точке ее непрерывность в этой точке?

Если функция U=f(x) дифференцирована в некоторый точке x=x₀, то она непрерывна в этой точке.

Это условии необходимое, но недостаточное.

Доказательство: пусть функция u= f(x) дифференцирована, тогда существует =а, тогда =а+(x), где (x) – б.м.

Тогда y=xа + x(x), y = ( f ’(x₀) x +x) = 0 в силу непрерывности.

33. Сформулируйте и докажите теорему о производной суммы двух функций.

Производная суммы двух функций равна сумме их производных.

Док-во: пусть f(x)= u + v – t, тогда

= = + -

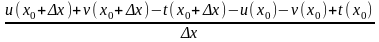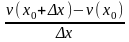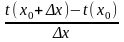
= u’+v’-t’ чтд

34. Сформулируйте и докажите теорему о производной произведения двух функций.

Если 2 функции U и V дифференцированы в некоторой точке, то тогда ф-я, равная Y=U+V, также будет иметь производную, равную Y’=U’V+UV’

Док-во:

Y= =

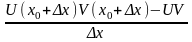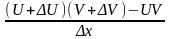
Т.к. U(x₀+x)= U + U = U(X₀)+U, аналогично для V

Раскрываем скобки и группируем

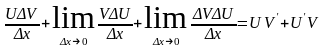
35. Сформулируйте теорему о производной обратной функции.С помощью этой теоремы найдите производную функции y=arcsinx в точке x₀ є (−1, 1).

Теорема. Если задана функция y=f(x) и для нее существует обратная функция x=g(y), которая в рассматриваемой точке у имеет производную g(x), не равную нулю, то в соответствующей точке x функция y=f(x) дифференцируема и f(x₀)=1/g(y₀)

y=arcsinx, x₀ є (−1, 1).

-/2 arcsinx/2, функция монотонная и непрерывна и меет обратную x=siny, x’=cosy, y’(x)=1/x(y) => y’(x)=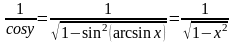

Дайте определение дифференциала функции f (x) в точке x0. Используя дифференциал, найдите приближенное значение величины:

36. .

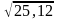Дифференциалом функции в точке х₀ называется главная линейная часть приращения функции в этой точке

При x0, dy=y’x или

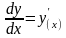
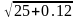= , 25= x₀, 0,12=x => f(x)= => f’(x)=1/10

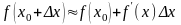
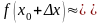5+0.1*0.12=5.012

37. ln1,09.

Дифференциалом функции в точке х₀ называется главная линейная часть приращения функции в этой точке

При x0, dy=y’x или

ln(1+0,09)= ln1+1*0.09=0.09

Дайте определение эластичности функции в точке. Найдите эластичность функции f (x) в точке x0:

38. f(x) = x⁴ , x₀ = 9.

Эластичностью функции y = f(x) в точке х₀ называется предел

f (x) = x⁴ => E(x)=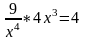 , при x₀ = 9.

39. f(x) = 3^x , x₀ = 5.

Э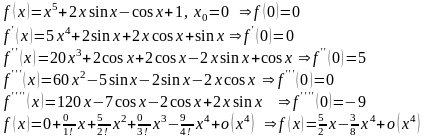 ластичностью функции y = f(x) в точке х₀ называется предел

E(x)=

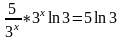
40. Докажите, что эластичность произведения двух функций равна сумме их эластичностей.

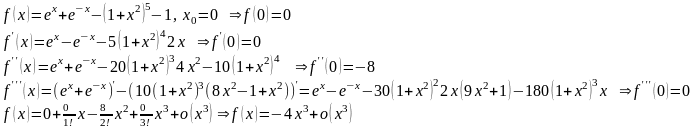Э ластичность произведения ф-и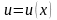й и 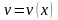в точке 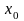равна сумме эластичностей ф-ций в этой же точке: 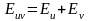. Эластичность равна E_y=x(lny)

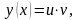Док-во: Пусть тогда .

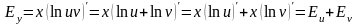41. Дайте опред и сформул необх усл лок экстремума ф-ии одной переменной. Прив прим ф-ии, для котор это усл выполнено в нек т, но экстремум отсутствует.

Точками локального экстремума явл. точки локального максимума (минимума). Точкой локального максимума точка явл. если существует окрестность т. М_о, в которой для любой точки М(x,y) выполняется неравенство f(M)f(M₀)

Необходимое условие: если f’(x,y) имеет частные производные 1-ого порядка в точке локального экстремума M₀(x,y), то

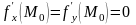
Пример: y=x³

42. Сформулируйте теорему Ролля. Можно утвержд, что производная функции f(x) = (x-2)(x-3)(x-4)(x-5) обращается в нуль в трех точках интервала (2,5)?

Пусть ф-ция 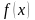непрерывна на отрезке [a;b], дифференцируема на интервале (a;b) и , то найдётся хотя бы одна точка , в которой .

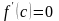Можно.

f(2)=0, f(3)=0, f(4)=0, f(5)=0 => существует С1из (2;3), такое, что f'(C1)=0, и тд 2, 3, 5, 4

43. Сформулируйте теорему Лагранжа. Докажите, что если f ′(x) = 0 на интервале (a,b), то функция f (x) постоянна на этом интервале.

Пусть функция f(x)

1. непрерывна на отрезке [a, b];

2. дифференцируема в интервале (a, b).

Тогда существует точка с О (a, b) такая, что f(b) − f(a) = f '(c) · (b − a)

 

=>

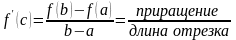
44. Используя теорему Лагранжа, докажите, что если f ‘(x) >0 на интервале (a,b) , то функция f (x) возрастает на этом интервале.

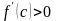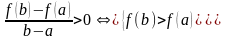=> возрастает.