11.Задачи приводящие к уравнению Лапласа

К уравнениям эллиптического типа приводит изучение стационарных, не меняющихся от времени, процессов различной физической природы. Это, например, стационарное тепловое поле, стационарная диффузия, электростатическое поле, стационарное магнитное поле, поле постоянного электрического тока, потенциальное движение несжимаемой жидкости.

В неоднородной, но изотропной среде основное уравнение стационарного поля – уравнение эллиптического типа

div(k grad u) = 0   

или, что то же самое,

,

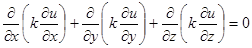где   – характеристика среды.

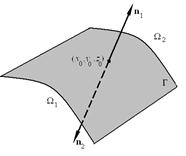
Если коэффициент   терпит разрыв на некоторой поверхности  , то на этой поверхности выполняются условия сопряжения

,

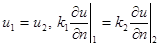где  ,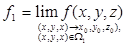

  .

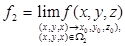Простейшие уравнения эллиптического типа – уравнение Лапласа

 и уравнение Пуассона  .

Функции, удовлетворяющие уравнению Лапласа, называются гармоническими функциями.

Если   – аналитическая функция комплексного переменного, то её действительная  и мнимая  части (  и  ), удовлетворяют уравнению Лапласа:  ,  .Такие функции  и   называют сопряжёнными гармоническими функциями.

В силу основной интегральной формулы Грина

,  ,  ,

,  , 

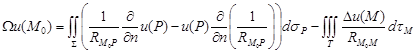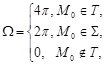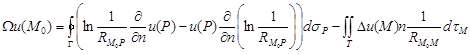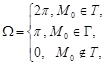
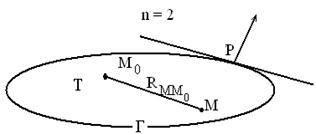
для гармонической в области  функции имеет место интегральное представление

:  , ,

:  ,

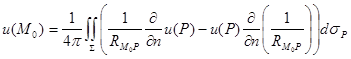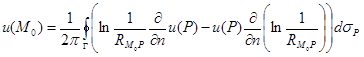Т.е. значение гармонической функции в любой внутренней точке области выражается через значение функции и её нормальной производной на границе области.

 

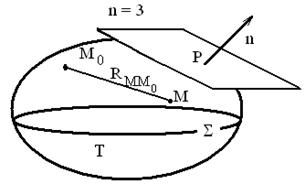
В зависимости от типа граничных условий для уравнений Лапласа и Пуассона формулируют три основные краевые задачи:

 

- первую краевую задачу (задачу Дирихле),     ;

- вторую краевую задачу (задачу Неймана,  ;

- третью краевую задачу,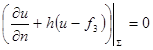         

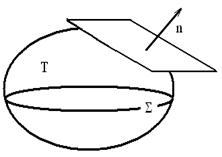
Здесь  ,  ,  ,   — функции, заданные на  ,   – производная в направлении внешней нормали к  .

12.Задачи Неймана и Дирихле

Задача Неймана

Зада́ча Не́ймана, вторая краевая задача — в дифференциальных уравнениях краевая задача с заданными граничными условиями для производной искомой функции на границе области — так называемые граничные условия второго рода. По типу области задачи Неймана можно разделить на два типа: внутренние и внешние.

Внутренняя задача Неймана

Внутренняя задача Неймана заключается в нахождении гармонической в ограниченной области G функции u,  , и удовлетворяющей на границе области G следующему краевому условию:

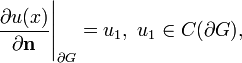
где n — внешняя единичная нормаль к границе области G.

Из теории потенциала известно, что необходимым условием разрешимости внутренней задачи Неймана является выполнение равенства

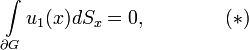
при этом решение внутренней задачи Неймана может быть найдено лишь с точностью до константы.

Внешняя задача Неймана

На неограниченных областях G в постановке задачи Неймана добавляется дополнительное условие ограниченности на бесконечности искомой функции u. Решение внешней задачи Неймана в пространстве размерности n>2 единственно, если на бесконечности функция u→0. В двумерном случае решение может быть найдено с точностью до константы, если выполняется условие (*).

Задача Дирихле

Задача Дирихле — задача отыскания в области   евклидова пространства гармонической функции  , которая на границе   области   совпадает с наперёд заданной непрерывной функцией  . Задачу отыскания регулярного в области решения эллиптического уравнения 2-го порядка, принимающего наперед заданные значения на границе области, также называют задачей Дирихле, или первой краевой задачей.