10.Распростронение тепла в неограниченном стержне. Интервал Пуасснова

Пусть в начальный момент задана температура в различных сечениях неограниченного стержня. Требуется определить распределение t в стержне в последующие моменты времени.

К таким задачам распространения тепла сводится физическая задачи в том случае когда стержень сталь длиной что температура во внутренних точках стержня мало зависит от условия на концах стержня.

Пусть стержень расположен по оси ОХ таким образом математическая задача формулируется следующим образом

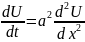(1)

В области ∞>х>-∞, t>0

Кроме этого должно удовлетворяться начальное условие

U(x,0)=U(x) (2)

Применим метод разделения переменных т.е будем искать частное решение уравнения (1)

U(x,t)=X(x)T(t) (3)

Подставим выражение (3) в (4)

X(x)T`(t)=a²X``(x)T(t) =>

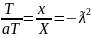(4)

Каждая из них не зависит не от х не от Т и обозначение их –ƛ²

Из (4)получим 2 уравнения

T`+ a²ƛ²T=0 (5)

x``+ƛ²x=0 (6)

Решаю уравнение (5)

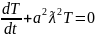
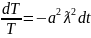
LnT=-a²ƛ²t+с

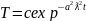
Решением (6) уравнения

Х=Аcosƛx+Bsinƛx

Подставляя в (3) получим

U(x,t)=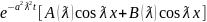 (7)

Постоянная с включена в А и В

Для каждой ƛ мы получим решение вида(7)

Произвольная постоянная для А и В каждого значения ƛ имеет определенное значение, поэтому А и В функция от ƛ

В силу линейности (1) решением является сумма решений вида (7)

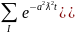
Проинтегрируем:

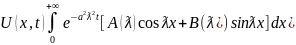(8)

Этот интеграл существует если производная по t и 2я производная по х существуют

Подберем A(ƛ) и В(ƛ) так чтобы U(x,t) удовлетворяет начальному условию (2)

Положим теперь в (8) t=0 и тогда используя условие (2) получим

U(x,0)= (9)

Предположим что такая что можно представить интегралом Фурье

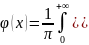
Разложим cos по формулам тригонометрии и получим

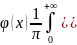(10)

Приравняем правые части (9) и (10) и получим

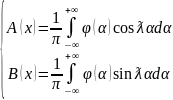(11)

Подставим найденное выражение в формулу для решения уравнения (8)

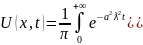или

(

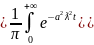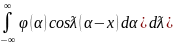
Или переставляя порядок интегрируя окончательно получим U(x,t)

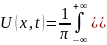(12)

Преобразуем (12) следующим образом:

Вычислим интеграл в круглых скобках

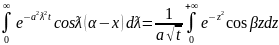(13)

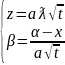(14)

Обозначаем данный интеграл через k(β)

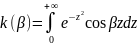(15)

Продифференцируем (15) как функцию β

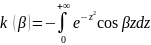
Проинтегрируем данный интеграл по частям:

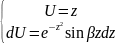
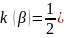
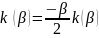
(16)

Определим постоянную С

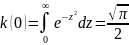
Следовательно в (16)

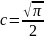
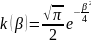(17)

Подставим (17) в (15) и получим

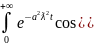
Заменим 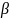по формуле (14) и получим

(18)

Подставим (18) в (12) и окончательно получим

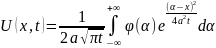(19)

Мы получили формулу (19) назыв интегралом Пуасона, представляющую собой решение представленной задачи в неограниченном стержне

Замечание: Можно доказать что функция U(x,t) определяется интегралом (19) является решением уравнения (1) и удовлетворяет условию (2) если 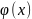ограничено на интервале (-∞;+∞)

Физический смысл (19)

Рассмотрим функцию

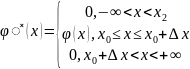(20)

Тогда функция

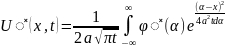(21)

Функция есть решение уравнения (1) принимает решение

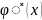
Принимаем во внимание (20) запишем что

U̽(x,t)=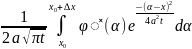

Применяя теорему о среднем получим

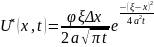(22)

X₀<𝞷<x₀+Δx

Сумма температур вида (22) дает решение (19)