
- •1.Уравнение в частных производных
- •2.Основные типы уравнений
- •3.Линейное однородное ду в частных производных первого порядка
- •4.Вывод уравнения колебаний струны методом Фурье
- •5.Задачи Коши
- •6.Решение уравнений колебаний струны методом Фурье
- •7.Решение волнового уравнения методом д′Аламбера
- •8.Уравнение теплопроводности для однородного стержня
- •9.Уравнение теплопроводности в пространстве
- •10.Распростронение тепла в неограниченном стержне. Интервал Пуасснова
- •11.Задачи приводящие к уравнению Лапласа
- •12.Задачи Неймана и Дирихле
- •Внешняя задача Неймана
- •13.Решение задачи Дирихле для уравнения Лапласа в круге методом Фурье
- •14.Случайное событие. Относительная частота случайного события. Вероятность события.
- •15.Теорема я.Бернулли
- •16.Совместные и несовместимые события. Полная группа парами несовместимых событий
- •17.Геометрическая интерпретация событий
- •18.Операции над событиями
- •19.Аксиомотическое определение вероятности
- •20.Теорема о сложении вероятностей. Примеры
- •21.Геометрическая интерпретация вероятностей. Вывод формулы для суммы совместимых событий
- •22.Умножение вероятностей
- •23.Условная вероятность
- •Определение
- •Замечания
- •24.Полная вероятность. Формула Байеса
- •25.Дискретные случайные величины и их характеристики
- •26.Относительная частота и вероятность для дискретных случайных величин
- •27.Математическое ожидание дискретной случайной величины
- •28.Дисперсия, средневековое отклонение, моменты дискретной случайной величины
- •Определение
- •Замечания
- •Свойства
- •29.Непрерывные случайные величины. Функция распределения и плотности вероятности
- •30.Теорема о связи функции распределения с плотностью вроятности
- •31.Интегральный закон распределения. Интегральная кривая
- •32.Числовые характеристики непрерывных случайных величин
- •33.Медиана и мода
- •34.Нормальный закон распределения
- •35.Медиана и мода нормального закона распределения
- •36.Интеграл вероятностей
- •37.Свойства интеграла вероятностей
- •38.Функция Лапласа
- •39.Среднее отклонение и средняя ошибка
- •40.Приведенная функция Лапласа
- •41.Правило трех сигм
- •42.Закон больших чисел. Предельные теоремы
- •43.Задачи математической статистики. Выборка, эмпирическая функция распределения
- •44.Статистический ряд и гистограмма
- •45.Среднее взвешенное и статистическая дисперсия
- •46.Точечные оценки
- •47.Распределение Пуасона
- •48.Распределение Стьюдента
- •49.Основные свойства точечной оценки
- •50.Исправленная выборочная дисперсия
- •51.Стандартная ошибка среднего арифметического
- •52.Интервальные оценки параметров распределения
- •53.Доверительный интервал, границы
- •54.Проверка статистических гипотез
- •55.Корреляционный анализ
- •56.Регрессионный анализ
25.Дискретные случайные величины и их характеристики
В
одном и том же случайном эксперименте
можно рассматривать не одну, а несколько
- n -
числовых функций, определенных на одном
и том же пространстве элементарных
событий. Совокупность таких функций
называется многомерной
случайной величиной или случайным
вектором и
обозначается ![]() .
.
Точнее.
На вероятностном пространстве ![]() заданы
случайные величины
заданы
случайные величины ![]() ;
каждому w
;
каждому w ![]() W эти
величины ставят в соответствие n-мерный
вектор
,
который называется n-мерным случайным
вектором (n-мерной
случайной величиной).
W эти
величины ставят в соответствие n-мерный
вектор
,
который называется n-мерным случайным
вектором (n-мерной
случайной величиной).
Многомерные случайные величины. Функции распределения многомерных случайных величин.
Функцией
распределения случайного
вектора
или совместным
распределением случайных величин ![]() называется
функция, определенная равенством
называется
функция, определенная равенством
![]() ,
,
где ![]() .
.
По
известной многомерной функции ![]() можно
найти распределение каждой из компонент
можно
найти распределение каждой из компонент ![]() .
.
Например,
если ![]() -
двумерная случайная величина, имеющая
совместное распределение
-
двумерная случайная величина, имеющая
совместное распределение ![]() ,
то распределения компонент
,
то распределения компонент ![]() и
и ![]() вычисляются
соответственно по формулам:
вычисляются
соответственно по формулам:
![]() ,
, ![]() .
.
В дальнейшем будем рассматривать двумерные случайные векторы.
Случайный
вектор ![]() называется непрерывным
случайным вектором,
если существует такая неотрицательная
функция
называется непрерывным
случайным вектором,
если существует такая неотрицательная
функция ![]() ,
что для любого прямоугольника W
на плоскости
,
что для любого прямоугольника W
на плоскости ![]() вероятность
события
вероятность
события ![]() равна
равна
![]() .
.
Функция в этом случае называется совместной плотностью распределения.
Легко
показать, что ![]() .
.
Если - совместная плотность распределения двумерного случайного вектора , то плотности распределения его компонент определяются равенствами:
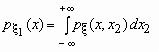 и
и 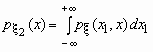 .
.
Если ![]() -
дискретный случайный вектор, то совместным
распределением случайных величин
-
дискретный случайный вектор, то совместным
распределением случайных величин ![]() и
и ![]() чаще
всего называют таблицу вида
чаще
всего называют таблицу вида
|
y1 |
y2 |
... |
ym |
x1 |
p11 |
p12 |
... |
p1m |
x2 |
p12 |
p12 |
... |
p2m |
... |
... |
... |
pij |
... |
xn |
pn1 |
pn2 |
... |
pnm |
где ![]() и
и ![]() .
.
По
этой таблице можно найти
распределения ![]() и
и ![]() компонентx и h .
Они вычисляются по формулам:
компонентx и h .
Они вычисляются по формулам:
![]() .
.
Независимость случайных величин
Решить обратную задачу, т.е. восстановить совместное распределение (x , h ) по распределениям величин x и h , вообще говоря, невозможно. Однако эту задачу можно решить, когда случайные величины x и h независимы.
Случайные величины x и h называются независимыми, если для любых x1, x2 R2справедливо равенство:
Fx ,h (x1, x2)= Fx (x1)Fh ( x2).
Для непрерывных случайных величин это определение эквивалентно следующему:
случайные величины называются независимыми, если
px ,h (x1, x2)= px (x1) ph (x2)
во всех точках непрерывности входящих в это равенство функций.
Для дискретных случайных величин x и h с матрицей совместного распределения {pij} условие независимости x и h имеет вид:
pij = P(x = xi, h = yj) = P(x = xi) P(h = yj),
для всех i = 1, 2, …, n, j = 1, 2, …, m.
Условные распределения случайных величин
Если две случайные величины x и h зависимы, то информация о том, какое значение на самом деле приняла одна из них, меняет наше представление о распределении другой. В связи с этим можно ввести понятие условного распределения.
Условные распределения дискретных случайных величин
Пусть дана двумерная случайная величина (x ,h ) с распределением
|
y1 |
y2 |
... |
ym |
x1 |
p11 |
p12 |
... |
p1m |
x2 |
p12 |
p12 |
... |
p2m |
... |
... |
... |
pij |
... |
xn |
pn1 |
pn2 |
... |
pnm |
Тогда распределения случайных величин x и h имеют соответственно вид:
x |
x1 |
x2 |
... |
xn |
p |
p1· |
p2· |
... |
pn· |
h |
y1 |
y2 |
... |
yn |
|
p· 1 |
p· 2 |
... |
p· n |
точка · в индексе означает суммирование по строкам или по столбцам:
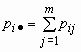 ,
, ![]() .
.
Условным
распределением случайной
величины
при
условии, что случайная величина
приняла
значение ![]() ,
называется распределение:
,
называется распределение:
x |
x1 |
x2 |
... |
xn |
p |
|
|
... |
|
Нетрудно
убедиться, что сумма вероятностей
величины
в
этом распределении равна единице: 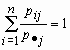 для
всех j =
1, 2, …, m.
для
всех j =
1, 2, …, m.
Совершенно
аналогично условным
распределением случайной
величины
при
условии, что случайная величина
приняла
значение ![]() ,
называется распределение:
,
называется распределение:
h |
y1 |
y2 |
... |
yn |
p |
|
|
... |
|
И  для
всех i =
1, 2, …, n.
для
всех i =
1, 2, …, n.
Если условные распределения случайных величин x и h отличаются от их безусловных распределений, то случайные величины x и h зависимы.
Условные распределения непрерывных случайных величин
Если ![]() -
плотность вероятностей совместного
распределения двумерной случайной
величины
,
то плотности вероятностей каждой ее
компоненты вычисляются по формулам:
-
плотность вероятностей совместного
распределения двумерной случайной
величины
,
то плотности вероятностей каждой ее
компоненты вычисляются по формулам:
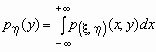 ,
, 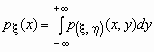 .
.
Условной плотностью распределения случайной величины x при условии, что случайная величина h принимает значение h = y0, называется функция переменной x, определяемая формулой
![]() .
.
Аналогично, условной плотностью распределения случайной величины при условии, что случайная величина x принимает значение x = x0, называется функция переменной y, определяемая формулой
![]() .
.
