1.Уравнение в частных производных

Определение: К ДУ частных производных относится уравнение относительных неизвестных функций нескольких переменных, ее аргумент и ее частн производная различных порядков

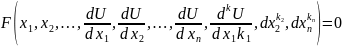
Порядком ДУ k›x производных называется порядок частных производных

Решением уравнения является некоторая функция U(x₁, x₂, ...., x_n) которая образует уравнение в тождество

Линейное однородное ДУ частных производных 1-го порядка

ДУ частных производных 1го порядка можно записать в виде

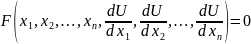
Линейное уравнение частных производных 1го порядка имеет вид

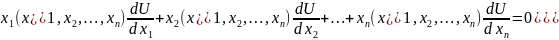(1)

Рассмотрим:

(2)

или

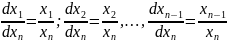(3)

Система (2) и (3) наз нормальной

Общее ренение имеет вид:

(1)

Если разрешить эти уравнения относительно постоянной С, мы получим:

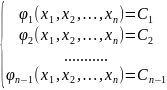(2)

Каждая из функций 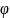является интегралом системы (2)

Теорема: Если 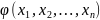есть интеграл системы (2) то функция является решением уравнения (1)

2.Основные типы уравнений

Основными уравнениями математической физики наз следующие ДУ с частными производными 2го порядка:

1.Волновое уравнение

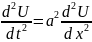(1)

a-некоторая константа

Это уравнение описывает множество физических процессов (поперечные колебания струны, продольные колебания стержня, электрические колебания в проводе, крутильные колебания вала и др.)

Это уравнение наз простейшим уравнением гиперболического типа

2.Уравнение теплопроводности(Фурье):

(2)

К исследованию этого уравнения приводит рассмотрение процессов распространения тепла, фильтрации жидкости и газа в пористой среде, в теории вероятности и др

это уравнение является простейшим уравнением параболического типа

3.Уравнение Лапласа

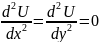(3)

Получено при рассмотрении задач в электрическом и магнитных полях, стационарным теплом состоянии, в задачах гидродинамики, диффузии и др. Является уравнением элиптического типа

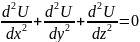
3.Линейное однородное ду в частных производных первого порядка

Пусть y ' = f (x, y) — дифференциальное уравнение. Пусть функция f (x, y) задана на некотором открытом множестве Г плоскости Р переменных х, у. Относительно функции f (x, y) будем предполагать, что она сама и её частная производная является непрерывными функциями на всём открытом множестве Г, тогда

для всякой точки (х0, у0) множества Г найдётся решение у = φ (х) уравнения, удовлетворяющее условию у0 = φ(х0);

если два решения у = φ (х) и у = ψ (х) уравнения совпадают хотя бы для одного значения х = х0, то есть, если φ(х0) = ψ(х0), то решения эти тождественно равны для всех тех значений переменного х, для которых они оба определены.

Числа (х0, у0) называются начальными значениями для решения y = φ(х), а соотношение у0 = φ(х0) — начальным условием этого решения.

Геометрическое содержание теоремы заключается в том, что через каждую точку (х0, у0) множества Г проходит одна и только одна интегральная кривая дифференциального уравнения.

Однородные дифференциальные уравнения первого порядка

Уравнение y ' = f (x, y) называется однородными, если правую часть уравнения можно преобразовать к виду

f(x, y) = g (y/x).

Алгоритм решения однородного уравнения:

y = u(x)·x.

u'·x + u = g(u).

u'·x = g(u) - u.

G(u) = ln | x | + ln c.