48.Распределение Стьюдента

Вторым из широко используемых специальных распределений является t-распределение Стьюдента, или просто t-распределение. Это распределение случайной величины:

где U — случайная величина, имеющая нормированное нормальное распределение; V — случайная величина с распределением  с v степенями свободы, t-распределение применяется при проверке статистических гипотез при малом объеме выборки. Эти вопросы рассмотрены в гл. 6. Форма t-распределения полностью определяется одним параметром — числом степеней свободы v.

Вид кривой плотности t-распределения показан на рис. 4.13. t-распределение симметрично при любом v и при v З0 переходит в нормальное с параметрами   = 0 и  .

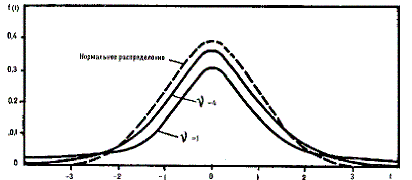
Рис. 4.13. t-распределение Стьюдента

Таблицы t-распределения обычно приводятся в приложениях к учебникам по ТВ.

49.Основные свойства точечной оценки

Свойства точечных оценок:

• Оценка 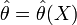называется несмещённой, если её математическое ожидание равно оцениваемому параметру генеральной совокупности:

,

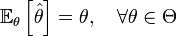• Оценка 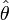называется эффективной, если она обладает минимальной дисперсией среди всех возможных несмещенных точечных оценок.

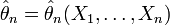• Оценка называется состоятельной, если она по вероятности с увеличением объема выборки n стремится к параметру генеральной совокупности: 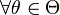, 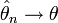по вероятности при .

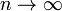• Оценка 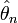называется сильно состоятельной, если , почти наверное при .

50.Исправленная выборочная дисперсия

Выборочная дисперсия является смещенной оценкой генеральной дисперсии, т.е. математическое ожидание выборочной дисперсии не равно оцениваемой генеральной дисперсии, а равно

  

  Для исправления выборочной дисперсии достаточно умножить ее на дробь

получим исправленную дисперсию S². Исправленная дисперсия является несмещенной оценкой.

В качестве оценки генеральной дисперсии принимают исправленную дисперсию.

Для оценки среднего квадратического генеральной совокупности используют исправленное среднее квадратическое отклонение

Замечание: формулы для вычисления выборочной дисперсии и исправленной дисперсии отличаются только знаменателями. При достаточно больших n выборочная и исправленная дисперсии мало отличаются, поэтому на практике исправленной дисперсией пользуются, если n<30.

 Вычислим выборочные характеристики по выборкам, рассмотренным в  лекции 12 пункт 3.1.(дискретный вариационный ряд и пункт 3.2.(интервальный вариационный ряд).

Пример 1. Для дискретного вариационного ряда:

Среднее выборочное

  

Выборочная дисперсия

  

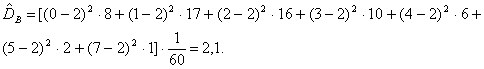
Выборочное среднее квадратическое отклонение

Исправленная дисперсия

Пример2. Для интервального вариационного ряда:

За  х_i примем середины частичных интервалов:

  

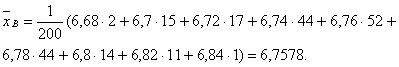
_{Для вычисления выборочной дисперсии воспользуемся формулой}

  

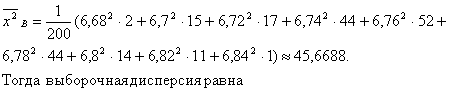
Выборочное среднее квадратическое отклонение :

51.Стандартная ошибка среднего арифметического

Отклонения оценок генеральных параметров от истинных значений этих параметров называются статистическими ошибками, или ошибками репрезентативности.

Величины статистических ошибок оценивают по среднему квадратическому (стандартному) отклонению выборочных характеристик. Если взять очень много независимых выборок объема n из одной и той же генеральной совокупности и определить для каждой из них среднее арифметическое, то окажется, что полученные средние арифметические варьируют вокруг своего среднего значения (равного μ) в раз меньше, чем отдельные варианты выборки. Т.е. стандартное отклонение выборочного среднего арифметического будет равно

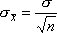
где σ — стандартное отклонение генеральной совокупности.

В качестве оценки стандартного отклонения выборочного среднего используется величина 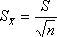называемая стандартной ошибкой среднего арифметического. В формуле (5.1) S — выборочное стандартное отклонение .

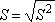Величина 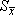показывает, какая ошибка в среднем допускается, если использовать вместо генерального среднего μ его выборочную оценку . Поэтому вычисленное среднее арифметическое часто указывают в виде чтобы оценить точность оценки х.

Из формулы (5.1) видно, как зависит стандартная ошибка от объема выборки n: с увеличением объема выборки n стандартная ошибка уменьшается пропорционально корню квадратному из n.