6.Решение уравнений колебаний струны методом Фурье

Метод разделения переменных или метод Фурье, является одним из наиболее распространенных методов решения уравнений с частными производными. Изложение этого метода мы проведем для задачи о колебаниях струны, закрепленной на концах.

Итак, будем искать решение уравнения ,

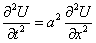(1)

удовлетворяющее однородным граничным условиямU(0, t) = U(l, t) = 0 U(0, t)= U(l, t) = 0 (2)

и начальным условиям.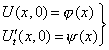 (3)

Уравнение (1) линейно и однородно, поэтому сумма частных решений также является решением этого уравнения. Будем искать решение уравнения в виде , 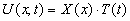(4)

где X(x)- функция только переменного ,

T(t)- функция только переменного .

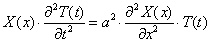
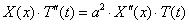
Подставим (4) в уравнение (1), получим: 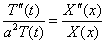(5)

Чтобы функция (4) была решением уравнения (1), равенство (5) должно удовлетворяться тождественно, то есть для всех значений независимых переменных , . Правая часть равенства (5) является функцией только переменного x, а левая- только .

Фиксируя, например, некоторое значение х и меняя t (или наоборот), получим, что правая и левая части (5) при изменении своих аргументов сохраняют постоянное значение, то есть.

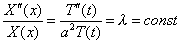(6)

Из соотношения (6) получаем обыкновенные дифференциальные уравнения для определения функций X(x) и T(t) .

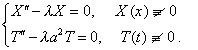(7) и(8)

Граничные условия (2) дают:

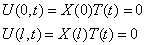
Отсюда следует, что функция X(x) должна удовлетворять дополнительным условиям X(0) =X(l) (9)

так как иначе мы имели бы T(t)≡0 и U(x, t)≡0, в то время как задача состоит в нахождении нетривиального решения.

Таким образом, в связи с нахождением функции X(x) мы приходим к простейшей задаче о собственных значениях: найти такие значения параметра λ, при которых существуют нетривиальные решения задачи: 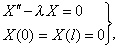(10)

а также найти эти решения. Такие значения параметра называются собственными значениями, а соответствующие им нетривиальные решения – собственными функциями задачи (10).

7.Решение волнового уравнения методом д′Аламбера

Найдем, в общем виде решение классической задачи Коши для однородного волнового уравнения в (уравнения свободных поперечных колебаний бесконечной струны)

в области с начальными условиями

Для справедливости дальнейших выкладок необходимо, чтобы и . Найдем функцию u(x,t) из класса , удовлеторяющую уравнению (1) и начальными условиями (2). Уравнение характеристик для уравнения (1) выглядит следующим образом

(dx)2 − a2(dy)2 = 0.

Его решение приводят к замене переменных

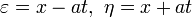
в результате которой исходное уравнение (1) принимает вид

Интегрируя два раза это уравнение (по и по η), находим

или

u(x,y) = I(x − at) + J(x + at),

где I,J - произвольные функции из класса .

Таким образом, решение задачи Коши (1)(2) является суммой прямой волны I(x − at)и обратной волны J(x + at).

Функции I и J легко выражаются через начальные условия (2):

I(x) + J(x) = u0(x)

− aI'(x) + aJ'(x) = u1(x)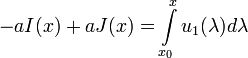

откуда

I(x) + J(x) = u0(x)

где x0 - произвольная фиксированная точка на прямой . Следовательно,

Итак, приходим к представлению

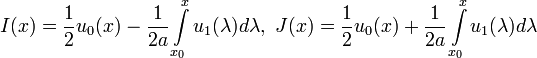
Эта формула, носящая имя Даламбера, и дает решение поставленной задачи.)