Расстояние между двумя скрещивающимися прямыми

В координатах

17. Взаимное расположение прямых (в одной плоскости, параллельно, скрещивающиеся)

2 ВАРИАНТА ОТВЕТА (НЕ ЗНАЮ, КАКОЙ ВЕРНЫЙ)

1.

Векторно-параметрическое уравнение прямой 

где   - фиксированная точка, лежащая на прямой;   - направляющий вектор (добавьте координаты z₀ и n в векторы r₀ и a соответственно).

Если прямые заданы уравнениями   и   то они:

1) параллельны (но не совпадают) 

2) совпадают 

3) пересекаются 

4) скрещиваются 

Если   то случаи 1 - 4 имеют место, когда (  - знак отрицания условия):

1)    

2)    

3)    

4)    

2.

Прямые   и  :

а) пересекаются 

б) параллельны (но не совпадают) 

в) совпадают 

Прямые   и  :

а) пересекаются 

б) параллельны (но не совпадают) 

в) совпадают 

Прямые   и  :

а) пересекаются 

б) параллельны (но не совпадают) 

в) совпадают 

18. Угол между прямыми, угол между прямой и плоскостью

Угол между двумя прямыми 

Угол между прямой и плоскостью 

19. Прямая на плоскости

Общее уравнение

Ax + By + C (  > 0).

Вектор   = (А; В) - нормальный вектор прямой.

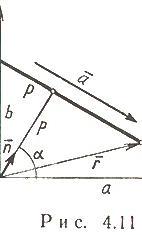
В векторном виде:   + С = 0, где   - радиус-вектор произвольной точки на прямой (рис. 4.11).

Частные случаи:

1) By + C = 0 - прямая параллельна оси Ox;

2) Ax + C = 0 - прямая параллельна оси Oy;

3) Ax + By = 0 - прямая проходит через начало координат;

4) y = 0 - ось Ox;

5) x = 0 - ось Oy.

Уравнение прямой в отрезках 

где a, b - величины отрезков, отсекаемых прямой на осях координат.

Нормальное уравнение прямой (рис. 4.11) 

где   - угол, образуемый нормально к прямой и осью Ox; p - расстояние от начала координат до прямой.

Приведение общего уравнения прямой к нормальному виду:

Здесь   - нормируемый множитель прямой; знак выбирается противоположным знаку C, если   и произвольно, если C = 0.

В координатах (параметрические уравнения):

Каноническое уравнение прямой 

Уравнение прямой по двум точкам (рис. 4.12) 

или

или

Уравнение прямой по точке и угловому коэффициенту (рис. 4.12)   или 

где   b - величина отрезка, отсекаемого прямой на оси Oy.

20. Кривые 2 порядка и их канонические уравнения

Канонические уравнения Окружность

Окружность радиуса R с центром в начале координат:

Уравнение касательной к окружности в произвольной точке  Параметрические уравнения: 

Окружность радиуса R с центром в точке C(a; b):

Эллипс (рис. 4.14) 

Пусть на плоскости заданы две точки   и     и дано число a (a > c). Эллипс - множество точек M плоскости, для каждой из которых сумма расстояний от точек   и   равна 2a. Точки   и   называются фокусами эллипса;   - большая ось;   - малая ось; O - центр;   - левый и правый фокусы;   - вершины; фокальные радиусы:

Каноническое уравнение: 

Гипербола (рис. 4.15) 

Пусть на плоскости заданы две точки   и     и дано число a (0 < a < c). Гипербола - множество точек M плоскости, для каждой из которых модуль разности расстояний от точек   и   равен 2a. Точки   и   называются фокусами гиперболы;   - действительная ось;   - мнимая ось; O - центр;   - левый и правый фокусы;   - вершины;   - фокальные радиусы: 

Каноническое уравнение: 

Парабола(рис. 4.16)

Пусть на плоскости заданы точка F и прямая  , не проходящая через F. Парабола - множество всех тех точек M плоскости, каждая из которых равноудалена от точки F и прямой  . Точка F называется фокусом, прямая   - директрисой параболы; (OF) - ось, O - вершина,   - параметр,   - фокус,   - фокальный радиус.

Каноническое уравнение: 

    

  

21. Обобщение рассмотренных ранее элементов. Линейное и векторное пространство (сформулировать аксиомы, привести примеры, арифметическое n-мерное векторное пространство)

22. Евклидово пространство (скалярное произведение и его свойства)

Нормированные векторные пространства

Понятие абсолютного значения распространяется на векторные пространства над нормированным полем K.

Нормой в векторном пространстве E называется отображение

удовлетворяющее следующим аксиомам:

1)  ;

2)  ;

3)   (неравенство треугольника).

Евклидово пространство

Пусть E - векторное пространство над полем R. Отображение

которое каждым двум элементам   ставит в соответствие действительное число, обозначаемое символом  , называется скалярным произведением, если   и   выполняются следующие аксиомы:

1)  ;

2)  ;

3)  ;

4)  .

Векторное пространство, в котором определено скалярное произведение, называется евклидовым пространством.

23. Скалярное произведение R_n. Неравенство Коши-Буняковского. Неравенство треугольника. Длина вектора и угол между векторами в R_n

Действительное линейное пространство E называется евклидовым, если каждой паре векторов  сопоставляется число   так, что   и   выполняются аксиомы:

     I. 

     II. 

     III. 

     IV. 

     Число   называют скалярным произведением векторов   и  ,   - скалярным квадратом вектора  (пишут  ). Введенная операция называется скалярным умножением векторов   и  .

     Длина вектора 

     Длина вектора   - число 

     Свойства:

     1) 

     2) 

     3)   (неравенство Коши-Буняковского);

     4)   (неравенство треугольника).

     Угол между векторами 

     Углом между векторами   и   называют угол  , для которого

ТУТ СРАЗУ 3 ВОПРОСА, ОНИ ФАКТИЧЕСКИ НЕРАЗДЕЛИМЫ

24. Понятие функции нескольких переменных (типы областей, ограничивающая точка, внутренние точки, геометрическая интерпретация функции нескольких переменных). Предел функции нескольких аргументов

25. Частные производные функции нескольких переменных

26. Дифференциал функции нескольких переменных. Правило дифференцирования сложных функций

Функции двух переменных  Приращение функции 

Функция, дифференцируемая в точке   

 при 

В этом случае дифференциал функции в точке  :

 - частные производные, вычисленные в точке  .

 Дифференцирование композиции 

1. Если   то

2. Если   то:

Однородная функция степени k 

Функции n переменных 

Приращение функции в точке   

Функция, дифференцируемая в точке     при 

 В этом случае дифференциал функции f в точке  :

 - частные производные первого порядка функции f.

Дифференцирование композиции  Если   то

27. Производная по направлению. Градиент функции

Градиент функции f 

Производная по направлению, определяемому вектором   

28. Уравнение касательной к плоскости и нормали к поверхности

Пусть дана некоторая поверхность, A — фиксированная точка поверхности и B — переменная точка поверхности, 

→

n

 — фиксированный вектор.

Обозначим j = j(M) — угол между векторами AB и 

Ненулевой вектор  называется нормальным вектором к поверхности в точке A, если

Точка поверхности F(x,y,z) = 0 называется обыкновенной, если в этой точке

1. частные производные F'_x , F'_y , F'_z непрерывны;

2. (F'_x)² + (F'_y)² + (F'_z)² ≠ 0 .

При нарушении хотя бы одного из этих условий точка поверхности называется особой точкой поверхности.

Теорема 1. Если M(x₀, y₀, z₀) — обыкновенная точка поверхности F(x,y,z) = 0 , то вектор

= grad F(x0, y0, z0) = F'x(x0, y0, z0)  + F'y(x0, y0, z0)  + F'z(x0, y0, z0)

является нормальным к этой поверхности в точке M(x₀, y₀, z₀) .

Нормалью к поверхности в некоторой ее точке называется прямая, направляющий вектор которой является нормальным к поверхности в этой точке и которая проходит через эту точку.

Канонические уравнения нормали можно представить в виде

Касательной плоскостью к поверхности в некоторой точке называется плоскость, которая проходит через эту точку перпендикулярно нормали к поверхности в этой точке.

Из этого определения следует, что уравнение касательной плоскости имеет вид:

F'x (x0, y0, z0)(x − x0) + F'y (x0, y0, z0)(y − y0) + F'z (x0, y0, z0)(z − z0) = 0.

Если точка поверхности является особой, то в этой точке нормальный к поверхности вектор может не существовать, и, следовательно, поверхность может не иметь нормали и касательной плоскости.