Министерство образования и науки Российской Федерации

Санкт-Петербургский национальный исследовательский

университет информационных технологий,

механики и оптики

(Университет ИТМО)

Региональная студенческая

математическая олимпиада

Санкт-Петербурга

2015 г.

Санкт-Петербург

2015

В 2000-2015 гг. студенческая олимпиада г. Санкт-Петербурга по математике проводилась Санкт-Петербургским национальным исследовательским университетом информационных технологий, механики и оптики (до 2011 года носившем название Санкт-Петербургский государственный университет информационных технологий, механики и оптики, СПбГУ ИТМО). В 2015 году каждый вуз мог выставить на олимпиаду одну или две команды по 3 человека (в командный зачет входили все участники команды) и студентов в личный зачет. В личном зачете участвовали все заявленные студенты. Результат вуза в командном зачете определялся по результату лучшей из его команд (если их две).

Олимпиада проводилась в воскресенье 25 октября 2015 года. На решение задач отводилось 4 часа. Пользоваться печатными или электронными справочниками не разрешалось. Студентам всех групп было предложено 12 задач. Каждая задача оценивалась в 10 баллов.

Председателем жюри был профессор В.Д. Лукьянов. В оргкомитет олимпиады входили: ректор Университета ИТМО чл.-корр. РАН Васильев В.Н., проректор по УО и АР проф., д.ф.-м.н. Колесников Ю.Л., руководитель СПИБ Гвоздев С.С., проф., д.ф.-м.н Попов И.Ю., доц., к.ф.-м.н. Фролов В.М., доц., к.т.н. Блинова И.В., к.ф.-м.н. Рыжков А.Е., к.ф.-м.н. Трифанова Е.С., к.ф.-м.н. Трифанов А.И.; ст. преп.: Родина Т.В., асс. Попов А.И., асс. Бойцев А.А., вед. инж. Коченюк Т.Г.

Составители: проф.: д.ф.-м.н. Лукьянов В.Д., д.ф.-м.н. Попов И.Ю.; доц.: к.ф.-м.н. Фролов В.М., к.ф.-м.н. Рыжков А.Е., к.ф.-м.н. Трифанова Е.С., к.т.н. Блинова И.В., к.ф.-м.н. Трифанов А.И.; ст. преп.: Родина Т.В., Петтай П.П.; асс. Попов А.И.

Задачи Региональной олимпиады с-Петербурга 2015 г.,

25.10.2015

1.Пусть и– некоторые точки. Известно, что. Найти скалярное произведение.

2. Найти все вещественные корни уравнения .

3. Найти все функции которые при любых действительныхудовлетворяют уравнению

4. Решить систему дифференциальных уравнений:

.

5. Вычислить интеграл .

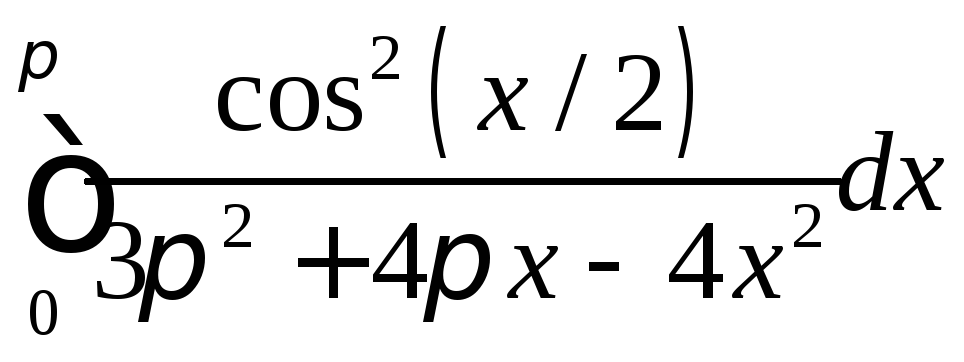6. Существует ли бесконечно дифференцируемая функция натакая, что последовательность, определенная рекуррентноудовлетворяет следующему условию при любых:

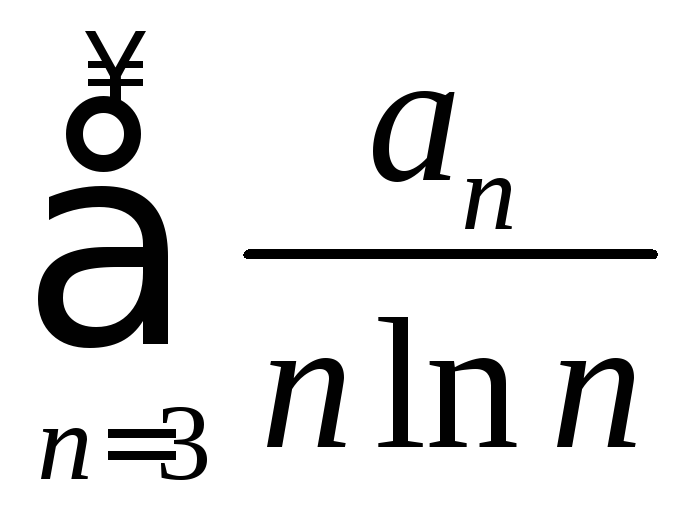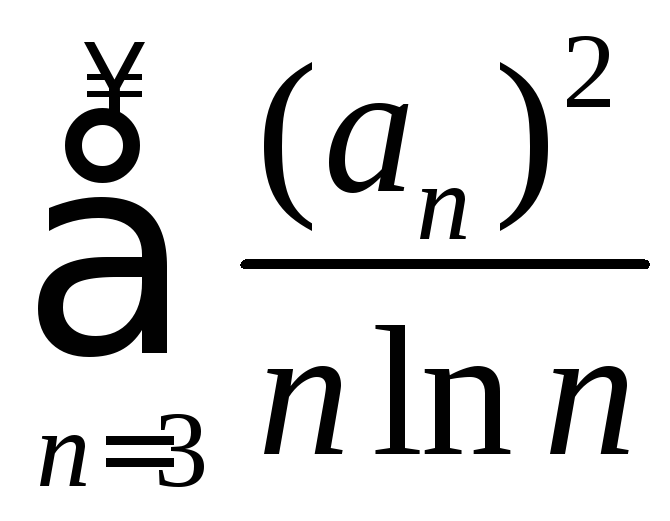- расходится, - сходится?

7. Доказать, что многочлен

имеет не более одного действительного корня.

8. Пусть функция определена и непрерывна на отрезке. Доказать, чтосуществует точкатакая, что.

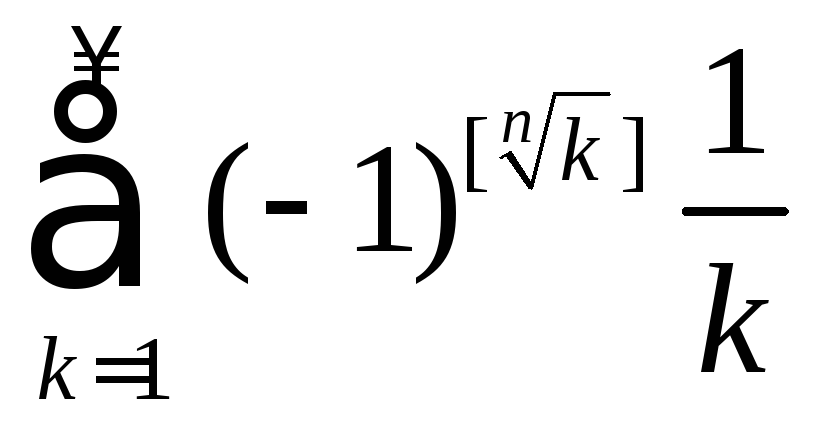9. Для каких натуральных ряд сходится? Здесь [z] обозначает наибольшее целое, меньшее или равное .

10. На плоскости с декартовыми координатами найти множество точек, из каждой из которых можно провести ровно три нормали к параболе .

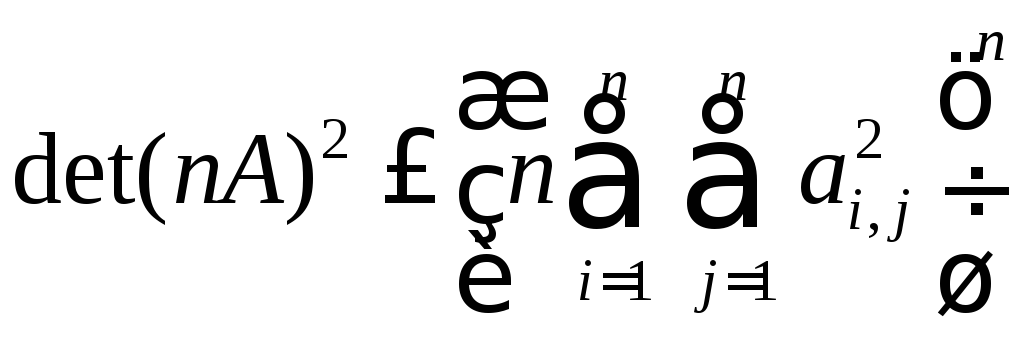11. Докажите, что для любой квадратной матрицы -ого порядка с вещественными элементамисправедливо неравенство:. Когда достигается равенство?

12. Найти все дважды дифференцируемые функции , удовлетворяющие уравнению, где.

Решения задач

1.Ответ:

Решение.

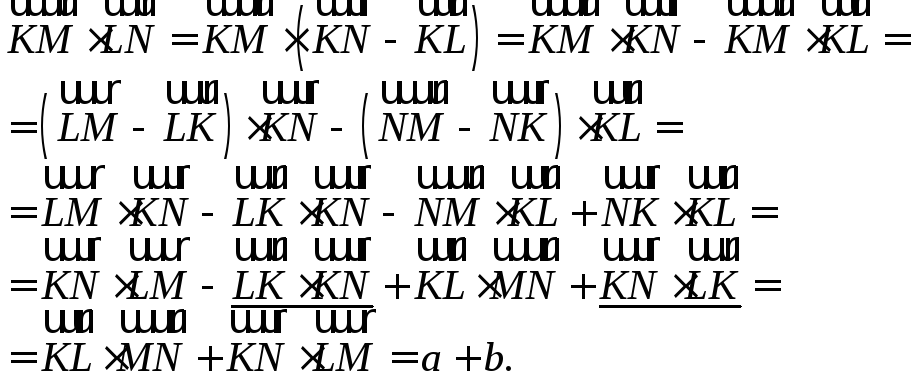
2. Ответ. Вещественных корней нет.

Решение. Очевидно, что ряд сходится абсолютно на всей вещественной оси.

.

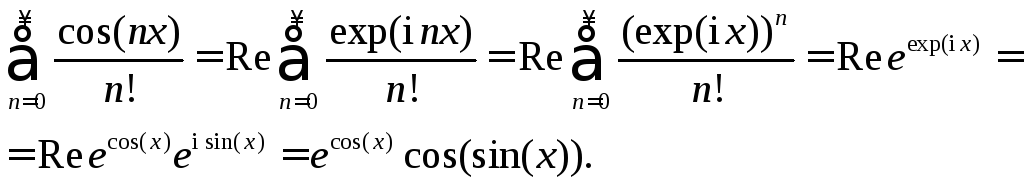Уравнение эквивалентно, однако, последнее уравнение вещественных корней не имеет, ибона вещественной оси по модулю не превосходит 1.

3.. Ответ: таких функций не существует.

Решение. Подставляя в данное функциональное уравнение, получаем. Это уравнение имеет два действительных корня:или. Полагая в функциональном уравненииполучаемилиЕслитоЕслитоПроверка показывает, что ни функцияни функцияне удовлетворяют данному функциональному уравнению, а, следовательно, это уравнение не имеет решений.

Замечание. Можно рассмотреть .

4. Ответ: .

Решение. Преобразуем данную систему, воспользовавшись свойством сложения пропорций:

Отсюда или

(2)

где произвольная константа.

Соотношение (2) – первый интеграл системы (1). Для того, чтобы найти ещё один первый интеграл данной системы, преобразуем второе уравнение системы (1):

, или в силу (2):.

Отсюда,

, (3)

где произвольная константа.

Очевидно, что первый интеграл (2) и первый интеграл (3) независимы. Следовательно, их система – общий интеграл данной системы дифференциальных уравнений.

5. Ответ:.

Решение.

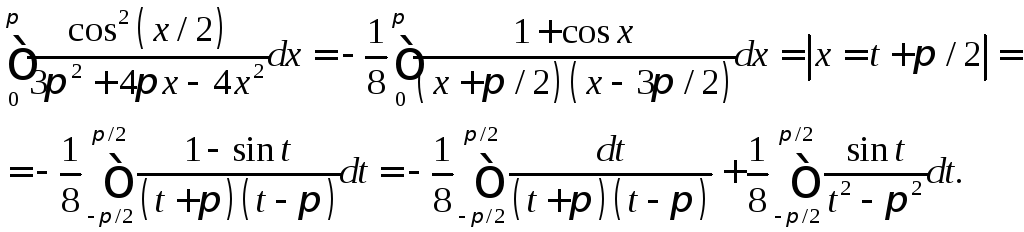
Поскольку

,

,

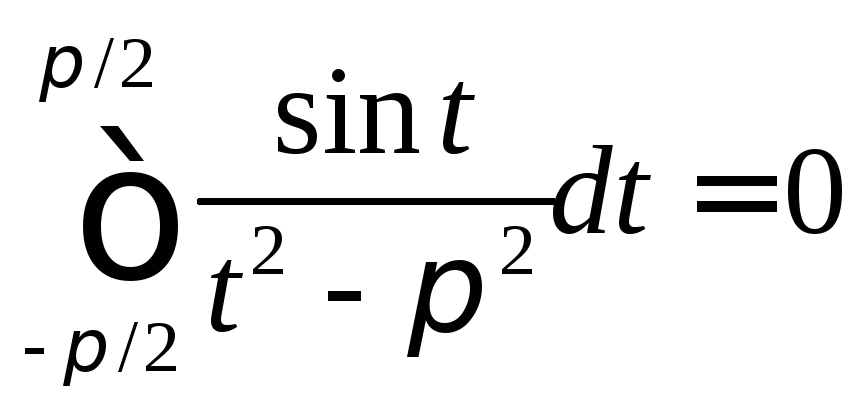то

.

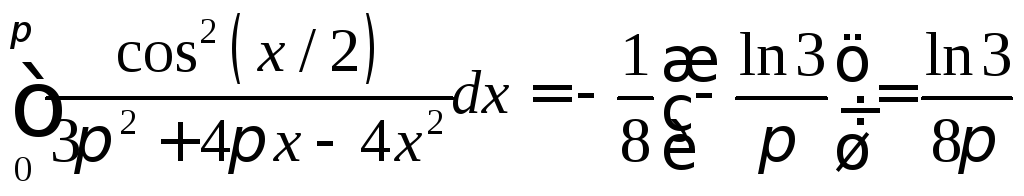6. Ответ. Да. Пример: .

Решение. Ясно, что последовательность обладает нужным свойством. (по интегральному признаку Коши). Построим функцию, которая генерирует последовательность с аналогичным поведением с помощью рекуррентного соотношения. Рассмотрим бесконечно дифференцируемую нафункциюи функциональное уравнение. Легко видеть, что функцияудовлетворяет этому уравнению. Здесь- это обратная функция к (она существует из-за монотонности ), - сдвиг на единицу аргумента функции. Соответственно,

.

Рекуррентное соотношение принимает вид .

Проверим, что это подходящая последовательность.

.

Это означает, что для любого . Выбранная функция подходит.

7. Решение. Пусть многочлен имеет более одного действительного корня (таких корней многочлен степенис действительными коэффициентами имеет не более чем), и пустьи– корни многочленатак что интервалне содержит других действительных корней данного многочлена. Отметим, чтои, так как многочленможет иметь лишь отрицательные корни. Поскольку

, то и, следовательно,,, а, значит, в точкахипроизводнаяимеет одинаковые знаки. Тогда в некоторой правой полуокрестности точкии некоторой левой полуокрестности точкимногочленбудет иметь разные знаки, а, следовательно, существует точкатакая, чтоПришли к противоречию. Это значит, что многочленимеет не более одного действительного корня, что и требовалось доказать.

8. Решение.

.

Так как функция непрерывна как функцияна отрезке, то согласно теореме о среднем для определённого интеграла существует точкатакая, что

.

Отсюда , где, что и требовалось доказать.

9. Ответ: Для любых натуральных .

Решение. Для это известно. Поэтому можно считать, что. Обозначим. Суммы групп последовательных слагаемых одинакового знака обозначим

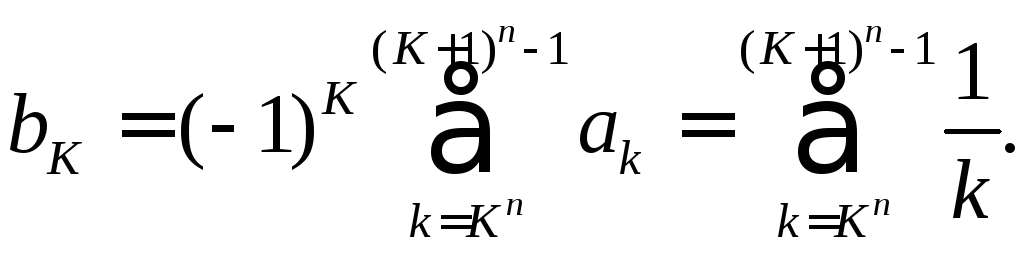
Покажем, что ряд 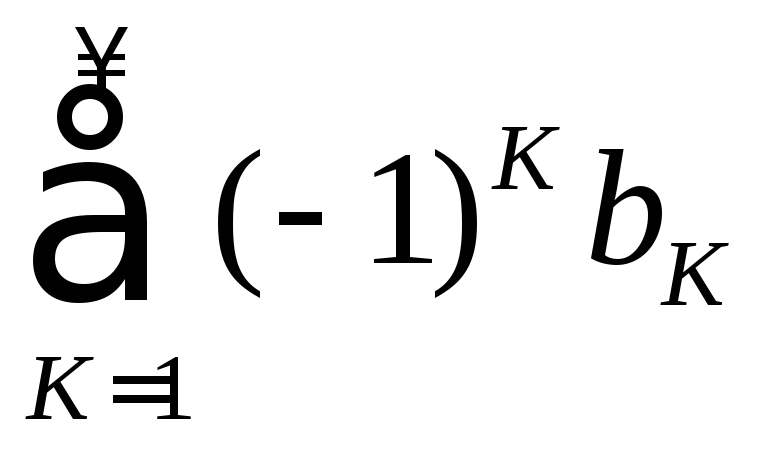сходится по признаку Лейбница и затем докажем из этого сходимость исходного ряда.

Требуется показать, что . для всех достаточно больших . Из-за монотонности функции имеем:

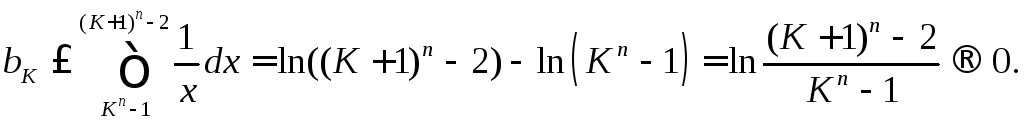
Предыдущая оценка для дает

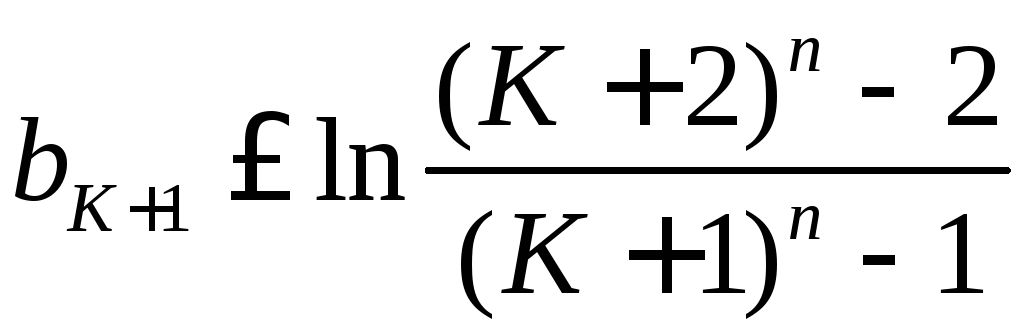
Аналогично находим

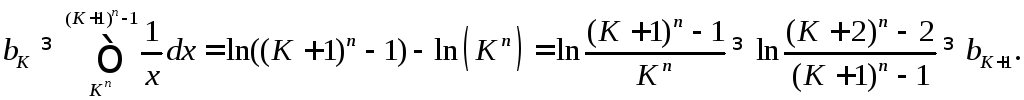Это следует из того, что

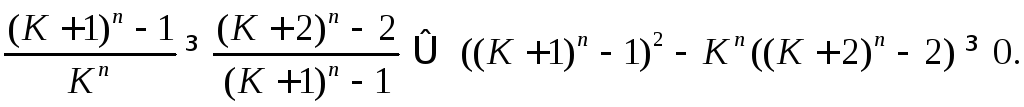
Если , то левая часть последнего неравенства равнаЕсли , то перепишем левую часть неравенства в виде

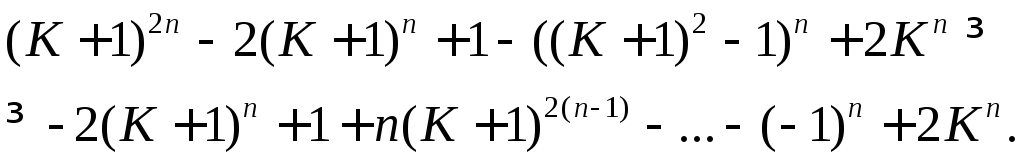
Последнее выражение положительно при достаточно больших , поскольку это полином от со старшим членом . Поэтому при достаточно больших и ряд сходится.

Чтобы показать сходимость исходного ряда, обозначим

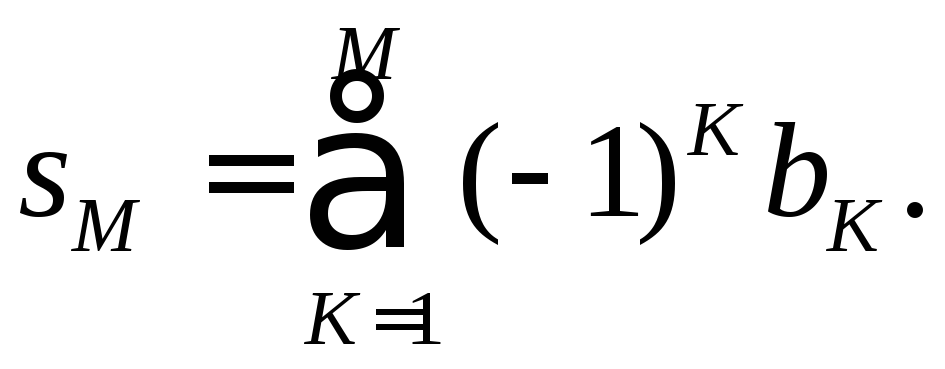
Фиксируем натуральное . Тогда для некоторого натурального имеем:Есличетно, тодля всех, и имеем

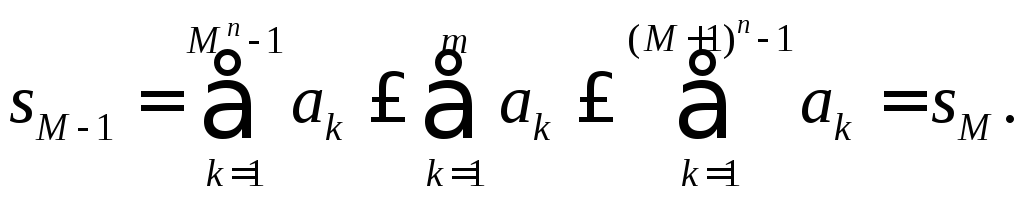
Если нечетно, тодля всех, и имеем противоположное неравенство

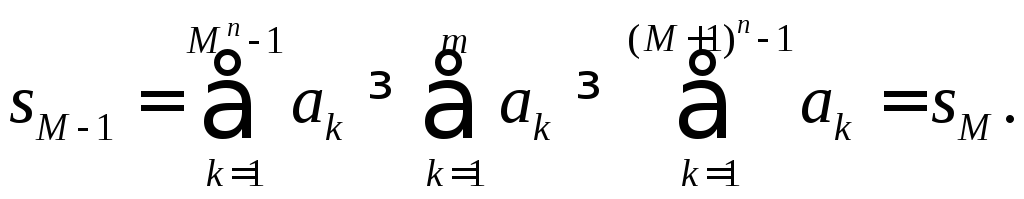
Итак, заключена между и , где при. Тогда

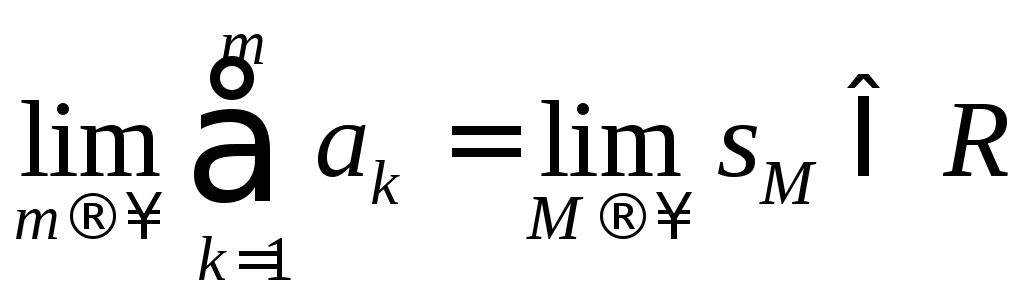
и сходимость ряда доказана.

10. Ответ: .

Решение. Проанализируем, для каких точек сколько нормалей имеется (это больше, чем спрашивается в задаче).

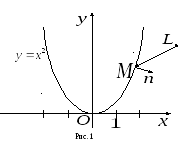
Пусть –произвольная точка плоскости, а –произвольная точка параболы (рис.1). За вектор нормали к параболе в точке можно взять вектор . Векторявляется вектором нормали к параболе в точке тогда и только тогда, когда векторы и коллинеарны, то есть если выполнено или . (1)

Подставляя в уравнение (1), получаем

. (2)

Таким образом, требуется найти множество точек ,для которых уравнение (2) имеет ровно три различных вещественных корня.

Если , тоуравнение (2) имеет ровно три различных вещественных корня при и один вещественный корень при(прикорень кратный).

Пусть .

Рассмотрим функцию .Тогда

Если , тозаисключением при.Тогда функция строго возрастает на всей числовой оси и поскольку , то прии произвольном уравнение (2) имеет один вещественный корень.

Если , топроизводная имеет два вещественных корня:

и .

В точке функцияимеет минимум, причем.

В точке функцияимеет максимум: .

Ясно, что уравнение (2) имеет ровно три различных вещественных корня тогда и только тогда, когда

, то есть ,или .

Если ,то есть ,или , тоуравнение имеет один вещественный корень, а если ,то есть ,или , то имеет ровно два различных вещественных корня.

Поскольку парабола симметрична относительно оси , то для получаются те же выводы, что и для .

Таким образом, в точке к параболе можно провести:

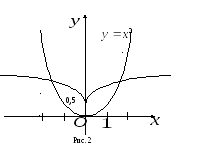
1) ровно три нормали тогда и только тогда, когда координаты точки удовлетворяют неравенствам

,;

2) ровно две нормали тогда и только тогда, когда координаты точки удовлетворяют равенствам

, .

3) ровно одну нормаль тогда и только тогда, когда координаты точки удовлетворяют неравенствам

, или (рис.2).