1. Матрицы. Линейные операции, их свойства

Матрицей размера называется прямоугольная таблица, содержащая m строк и n столбцов. Элементами матрицы могут быть числа, буквы (символы) и другие объекты.

Матрицы обозначают прописными (заглавными) буквами A, B, C, …, элементы матрицы – строчными буквами с двойной индексацией a_ij, где i - номер строки, j - номер столбца.

Виды матриц:

• матрица-строка;

• матрица-столбец;

• нулевая матрица;

• квадратная матрица;

• диагональная матрица (элементы по диагонали  0);

• единичная матрица (элементы по диагонали = 1, остальные = 0).

Операции над матрицами.

1. Умножение матрицы на число

Произведением матрицы A на число называется матрица ,элементы которой для Если , то (нулевая матрица того же размера).

2. Сложение матриц

Суммой матриц и одинакового размера называется матрица , элементы которой для

3. Вычитание матриц

Разность матриц одинакового размера определяется как .

4. Умножение матриц

Умножение матрицы на матрицу определено, когда число столбцов первой матрицы равно числу строк второй (условие согласованности). Тогда произведением матриц называется матрица , каждый элемент которой равен сумме произведений элементов -ой строки матрицы на соответствующие элементы -го столбца матрицы :

, где

Свойства операций сложения и умножения матриц.

1. .

2. .

3. .

4. .

5. .

6. .

7. .

8. (в общем случае). Кроме того, если существует, то может вообще не существовать.

9. , где - единичная квадратная матрица.

10. Произведение двух ненулевых матриц может равняться нулевой матрице, т.е. если , то не следует, что или .

2. Определители n-го порядка, их свойства, методы вычисления

Понятие определителя - число, характеризующее квадратную матрицу , необходимо для решения систем линейных алгебраических уравнений. Определитель матрицы обозначают , , .

Определителем матрицы 1-го порядка , называется элемент : ; Определителем матрицы 2-го порядка называется число, вычисляемое по формуле:

.

Произведения называются членами определителя 2-го порядка.

Определителем матрицы 3-го порядка называется число, вычисляемое по формуле:

.

Данная формула получила название правила треугольников или правило Сарруса.

При вычислении определителя 3-го порядка удобно пользоваться следующей схемой, показывающей произведения каких элементов берутся со знаком “+”, а каких со знаком “-“:

Определитель квадратной матрицы -го порядка (определитель -го порядка).

Рассмотрим квадратную матрицу n-го порядка. Зачеркнем элемент матрицы, стоящий на пересечении -й строки и -го столбца. В результате получается матрица порядка . Пусть дана матрица n-го порядка:

.

Минором элемента матрицы n-го порядка называется определитель матрицы -го порядка, полученной из матрицы вычеркиванием -й строки и -го столбца. Алгебраическим дополнением элемента матрицы -го порядка называется минор, взятый со знаком .

Теорема Лапласа. Определитель квадратной матрицы равен сумме произведений элементов любой строки (столбца) на их алгебраические дополнения:

(разложение по элементам -й строки; ).

(разложение по элементам -го столбца; ).

Свойства определителей.

1. Если какая-либо строка (столбца) матрицы состоит из одних нулей, то ее определитель равен 0.

2. Если все элементы какой-либо строки (столбца) матрицы умножить на число ,то ее определитель умножится на это число .

Замечание. За знак определителя можно выносить общий множитель любой строки (столбца) в отличие от матрицы, за знак которой можно выносить общий множитель всех элементов.

3. При транспонировании матрицы ее определитель не изменяется: .

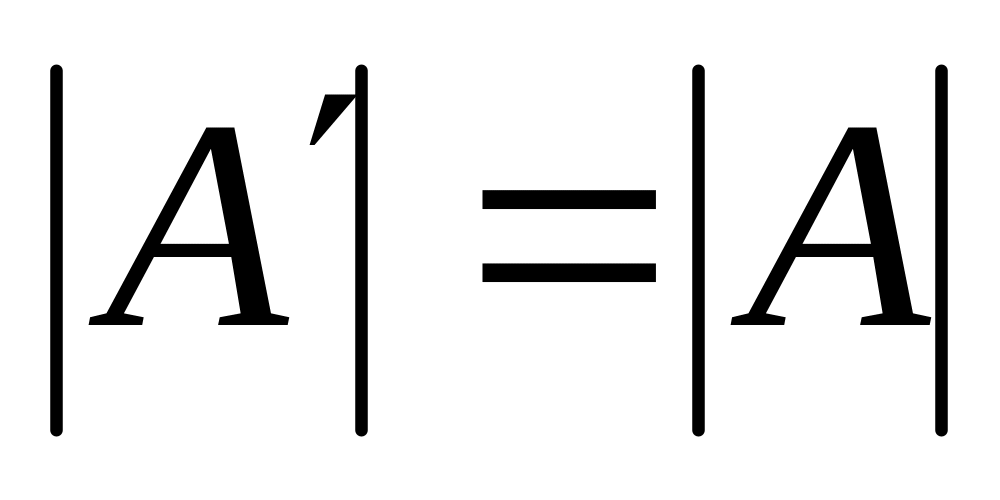4. При перестановки двух строк (столбцов) матрицы ее определитель меняет знак на противоположный.

5. Если квадратная матрица содержит две одинаковые строки (столбца), то ее определитель равен 0.

6. Если элементы двух строк (столбцов) матрицы пропорциональны, то ее определитель равен 0.

7. Сумма произведений элементов какой-либо строки (столбца) матрицы на алгебраические дополнения элементов другой строки (столбца) этой матрицы равна 0.

8. Определитель матрицы не изменится, если к элементам какой-либо строки (столбца) матрицы прибавить элементы другой строки (столбца), предварительно умноженные на одно и то же число.

9. Сумма произведений произвольных чисел 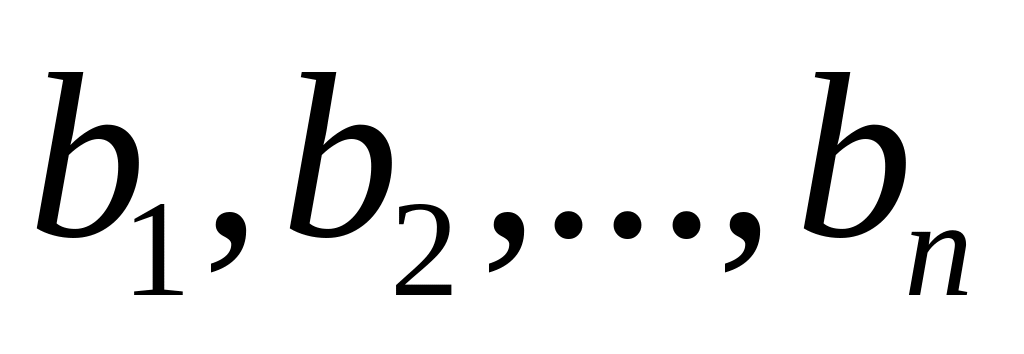на алгебраические дополнения любой строки (столбца) равна определителю матрицы, полученной из данной заменой элементов этой строки (столбца) на числа .

10. Определитель произведения двух квадратных матриц равен произведению их определителей: , где , а и - матрицы -го порядка.

Перечисленные свойства определителей позволяют существенно упростить их вычисления для определителей высоких порядков. При этом с помощью свойств 1-9 желательно преобразовать исходную матрицу таким образом, чтобы она имела строку (столбец), содержащую как можно больше нулей, а потом вычислить определитель, разложенный по этой строке (столбцу).

3. Обратная матрица и её свойства. Матричные методы решения уравнений

Для каждого числа существует обратное число такое, что произведение . Для квадратных матриц тоже вводится аналогичное понятие.

Матрица называется обратной по отношению к квадратной матрице , если при умножении этой матрицы на данную как справа, так и слева получается единичная матрица:

.

Только квадратная матрица может иметь обратную, однако не каждая квадратная матрица имеет обратную.

Матрица является невырожденной (неособенной), если , в противном случае при матрица называется вырожденной (особенной).

Теорема (необходимое и достаточное условие существования обратной матрицы). Обратная матрица существует (и единственна) тогда и только тогда, когда исходная матрица является невырожденной (неособенной) и вычисляется по формуле

,

где - присоединенная матрица, состоящая из алгебраических дополнений элементов транспонированной матрицы, т.е.

.

Необходимость. Пусть матрица имеет обратную , т.е. . По свойству 10 определителей имеем: , т.е. и .

Достаточность. Пусть . Рассмотрим квадратную матрицу n-го порядка , называемую присоединенной, элементы которой являются алгебраическими дополнениями элементов матрицы , транспонированной к . Тогда элементы произведения матриц определяются по правилу умножения матриц. Поэтому матрица В является диагональной, элементы ее главной диагонали равны определителю исходной матрицы. А произведение на равно той же матрице В: .

Единственность обратной матрицы. Предположим, что существуют еще матрицы и такие, что и , где матрица получена по формуле и выполняются равенства и . Тогда, умножая на слева первое из них, получаем: , откуда , т.е. . Аналогично, умножая второе равенство на справа, получаем . Единственность доказана.

Алгоритм вычисления обратной матрицы.

1. Находим определитель исходной матрицы. Если 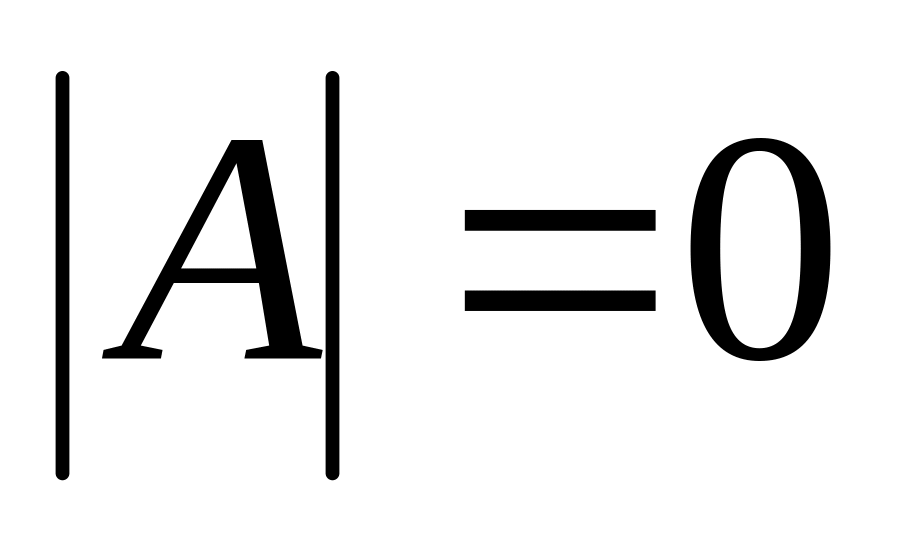, то матрица - вырожденная и обратной матрицы не существует. Если , то матрица невырожденная и обратная матрица существует.

2. Находим матрицу , транспонированную к .

3. Находим алгебраические дополнения элементов и составляем из них присоединенную матрицу .

4. Составляем обратную матрицу по формуле .

5. Проверяем правильность вычисления обратной матрицы , исходя из ее определения: .

4. Решение квадратных линейных систем (теорема Крамера, формулы Крамера)

Теорема Крамера. Пусть - определитель матрицы системы, а - определитель матрицы, получаемой из матрицы заменой -го столбца столбцом свободных членов. Тогда, если , то система имеет единственное решение, определяемое по формулам:

, - формула Крамера.

5. Метод Гаусса

Метод Гаусса - метод последовательного исключения переменных.

Метод Гаусса заключается в том, что с помощью элементарных преобразований строк и перестановок столбцов система уравнений приводится к равносильной системе ступенчатого (или треугольного) вида, из которой последовательно, начиная с последних (по номеру) переменных, находятся все остальные переменные.

Преобразования Гаусса удобно проводить не с самими уравнениями, а с расширенной матрицей их коэффициентов , получаемой приписыванием к матрице столбца свободных членов :

.

Следует отметить, что методом Гаусса можно решить любую систему уравнений вида .

СПЕЦИАЛЬНО ДЛЯ ПАСАНОВ!!!

Пример жопного Гаусса. Решить систему методом Гаусса:

Р е ш е н и е. Выпишем и преобразуем расширенную матрицу системы. Сначала прибавим к элементам третьей строки элементы первой строки, умноженные на –1. А затем элементы второй строки умножим на –1 и прибавим к элементам третьей строки:

.

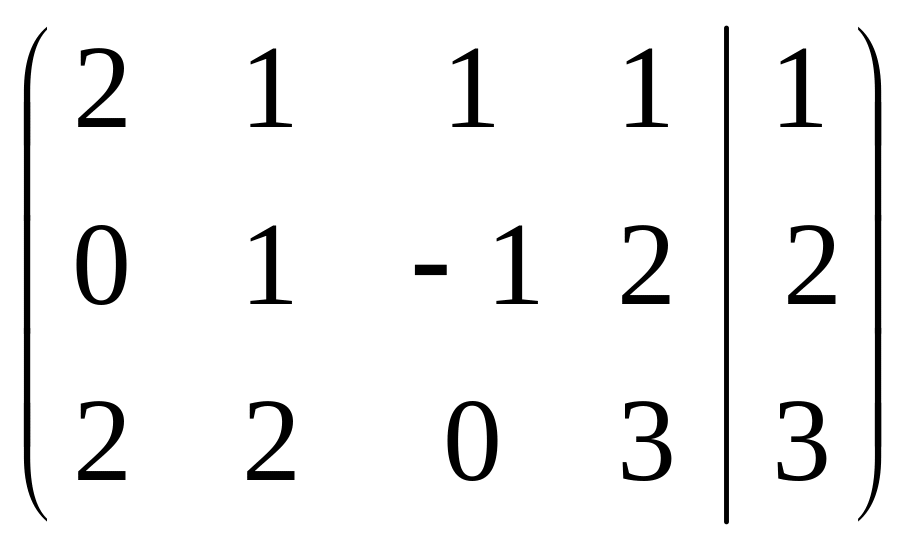
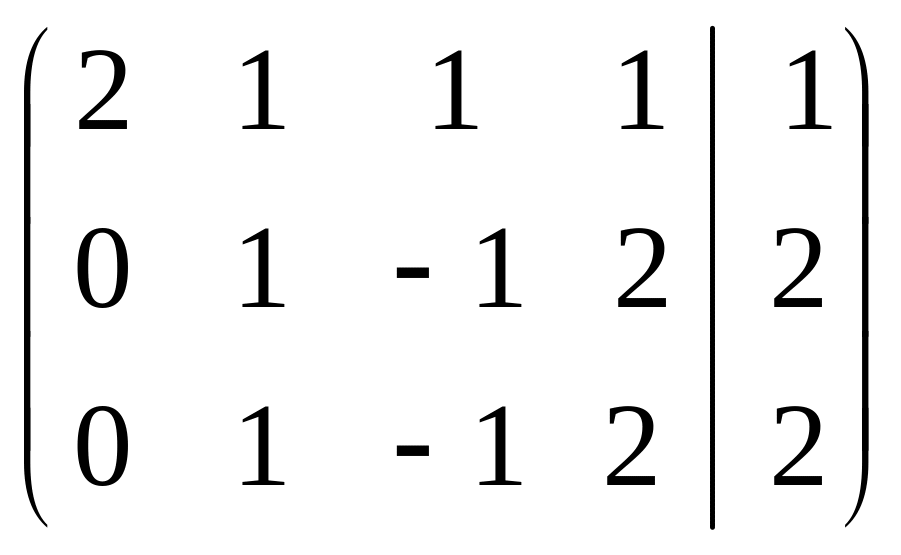
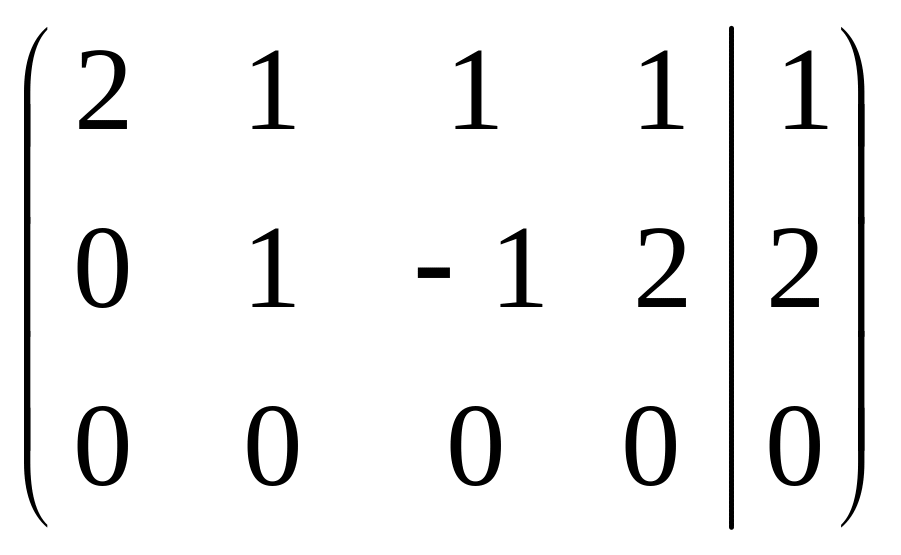Расширенная матрица приведена к ступенчатому виду.

. Так как ранг матрицы равен 2, а количество неизвестных равно 4, то система имеет бесконечное множество решений. В качестве базисных неизвестных возьмем и (т.к. определитель, составленный из их коэффициентов не равен нулю ), тогда и - свободные неизвестные.

Выразим базисные переменные через свободные.

Из второй строки полученной матрицы выразим переменную :

, .

Из первой строки выразим : ,

.

Общее решение системы уравнений: , .

6. Линейная зависимость и независимость строк, столбцов матриц. Ранг матрицы. Вычисление с помощью элементарных преобразований

Линейная независимость строк матрицы

Дана матрица размера

Обозначим строки матрицы следующим образом:

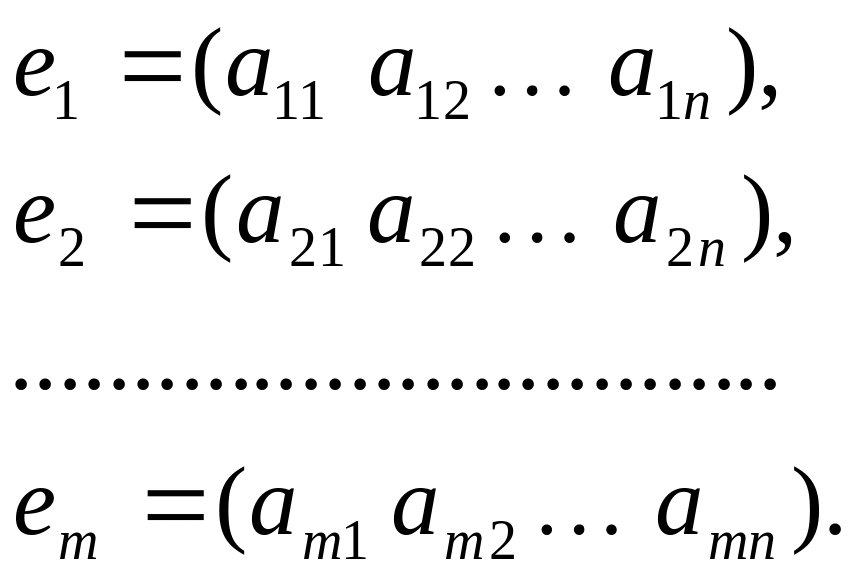
Две строки называются равными, если равны их соответствующие элементы. .

Введем операции умножения строки на число и сложение строк как операции, проводимые поэлементно:

.

Строка называется линейной комбинацией строк матрицы, если она равна сумме произведений этих строк на произвольные действительные числа (любые числа):

.

Строки матрицы называются линейно зависимыми, если существует такие числа , не равные одновременно нулю, что линейная комбинация строк матрицы равна нулевой строке:

, где . (1.1)

Линейная зависимость строк матрицы обозначает, что хотя бы 1 строка матрицы является линейной комбинацией остальных.

Если линейная комбинация строк (1.1) равна нулю тогда и только тогда, когда все коэффициенты , то строки называются линейно независимыми.

Для решения и исследования ряда математических и прикладных задач важное значение имеет понятие ранга матрицы.

В матрице размером вычеркиванием каких-либо строк и столбцов можно вычленить квадратные подматрицы -го порядка, где . Определители таких подматриц называются минорами -го порядка матрицы .

Например, из матриц можно получить подматрицы 1, 2 и 3-го порядка.

Определение. Рангом матрицы называется наивысший порядок отличных от нуля миноров этой матрицы. Обозначение: или .

Из определения следует:

1) Ранг матрицы не превосходит меньшего из ее размеров, т.е. .

2) тогда и только тогда, когда все элементы матрицы равны нулю, т.е. .

3) Для квадратной матрицы n-го порядка тогда и только тогда, когда матрица - невырожденная.

Поскольку непосредственный перебор всех возможных миноров матрицы , начиная с наибольшего размера, затруднителен (трудоемок), то пользуются элементарными преобразованиями матрицы, сохраняющими ранг матрицы.

Теорема о ранге матрицы. Ранг матрицы равен максимальному числу ее линейно независимых строк или столбцов, через которые линейно выражаются все остальные строки (столбцы).

Элементарные преобразования матрицы.

1. Отбрасывание нулевой строки (столбца).

2. Умножение всех элементов строки (столбца) на число .

3. Изменение порядка строк (столбцов) матрицы.

4. Прибавление к каждому элементу одной строки (столбца) соответствующих элементов другой строки (столбца), умноженных на любое число.

5. Транспонирование матрицы.

Матрица , полученная из матрицы при помощи элементарных преобразований, называется эквивалентной и обозначается А В.

Теорема. Ранг матрицы не изменяется при элементарных преобразованиях матрицы.

С помощью элементарных преобразований можно привести матрицу к так называемому ступенчатому виду, когда вычисление ее ранга не представляет труда.

Матрица называется ступенчатой если она имеет вид:

, где , , .

Очевидно, что ранг ступенчатой матрицы равен числу ненулевых строк , т.к. имеется минор -го порядка, не равный нулю:

.

7. Теорема Кронекера-Капелли по совместности решения алгебраических систем

Теорема Кронекера-Капелли. Система линейных уравнений совместна тогда и только тогда, когда ранг матрицы системы равен рангу расширенной матрицы этой системы: .