
- •Линейная зависимость и независимость строк, столбцов матриц. Ранг матрицы. Вычисление с помощью элементарных преобразований
- •Для совместных систем линейных уравнений верны следующие теоремы:
- •Линейные операции над любыми векторами удовлетворяют следующим свойствам:
- •Доказательство:
- •Расстояние между двумя скрещивающимися прямыми
- •Кривые 2 порядка и их канонические уравнения
- •Канонические уравнения Окружность
- •Необходимое и достаточное условие экстремумов
Для совместных систем линейных уравнений верны следующие теоремы:
Теорема 1.
Если ранг матрицы совместной системы
равен числу переменных, т.е.
![]() ,
то система имеет единственное решение.
,
то система имеет единственное решение.
Теорема 2.
Если ранг матрицы совместной системы
меньше числа переменных, т.е.
![]() ,
то система является неопределенной и
имеет бесконечное множество решений.
,
то система является неопределенной и
имеет бесконечное множество решений.
Базисным минором матрицы называется любой ненулевой минор, порядок которого равен рангу матрицы.
Те
неизвестных, коэффициенты при которых
входят в запись базисного минора,
называются базисными (или основными),
остальные
![]() неизвестных называются свободными (или
неосновными).
неизвестных называются свободными (или
неосновными).
Решить систему уравнений в случае - это значит выразить базисные переменные через свободные. При этом имеем общее решение системы уравнений. Если все свободные переменные равны нулю, то решение системы называется базисным (дальше жопный Гаусс из 5 вопроса).
Геометрические векторы. Линейные операции с векторами. Базис и координаты вектора, заданного базисом
Вектором называется
направленный отрезок
![]() с
начальной точкой А
и конечной точкой В
(который можно перемещать параллельно
самому себе).
с
начальной точкой А
и конечной точкой В
(который можно перемещать параллельно
самому себе).
Векторы могут обозначаться как 2-мя прописными буквами, так и одной строчной с чертой или стрелкой.
Длиной (или
модулем)
![]() вектора
называется
число, равное длине отрезка АВ,
изображающего вектор.
вектора
называется
число, равное длине отрезка АВ,
изображающего вектор.
Векторы, лежащие на одной прямой или на параллельных прямых, называют коллинеарными.
Если начало и конец
вектора совпадают (![]() ),
то такой вектор называется нулевым
и обозначается
),
то такой вектор называется нулевым
и обозначается
![]() =
.
Длина нулевого вектора равна нулю:
=
.
Длина нулевого вектора равна нулю:
![]() =
0.
=
0.
Произведением вектора на число
 :
:
Будет вектор,
![]() имеющий
длину
имеющий
длину![]() , направление которого совпадает с
направлением вектора
, направление которого совпадает с
направлением вектора
![]() ,
если
,
если
![]() ,
и противоположно ему, если
,
и противоположно ему, если
![]() .
.
Противоположным вектором - называется произведение вектора - на число (-1), т.е. - =
 .
.Суммой двух векторов и
 называется
вектор
называется
вектор
 ,
начало которого совпадает с началом
вектора
,
а конец с концом вектора
,
при условии, что начало
совпадает с концом
.
(правило треугольников). Аналогично
определяется сумма нескольких векторов.
,
начало которого совпадает с началом
вектора
,
а конец с концом вектора
,
при условии, что начало
совпадает с концом
.
(правило треугольников). Аналогично
определяется сумма нескольких векторов.
Разностью двух векторов и называется сумма вектора и вектора - , противоположного .
Линейные операции над любыми векторами удовлетворяют следующим свойствам:
1)
![]() -
коммутативное (переместительное)
свойство суммы;
-
коммутативное (переместительное)
свойство суммы;
2)
![]() -
ассоциативное (сочетательное) свойство
суммы;
-
ассоциативное (сочетательное) свойство
суммы;
3)
![]() -
ассоциативное относительно числового
множителя свойство;
-
ассоциативное относительно числового
множителя свойство;
4)
![]() - дистрибутивное (распределительное)
относительно суммы векторов свойство;
- дистрибутивное (распределительное)
относительно суммы векторов свойство;
5)
![]() - дистрибутивное относительно суммы
числовых множителей свойство;
- дистрибутивное относительно суммы
числовых множителей свойство;
6) Существует
нулевой вектор
![]() такой,
что
такой,
что
![]() для любого вектора
для любого вектора
![]() (особая роль нулевого вектора);
(особая роль нулевого вектора);
7) Для любого вектора
существует противоположный вектор
![]() такой, что
такой, что
![]() ;
;
8)
![]() для любого вектора
(особая роль числового множителя 1).
для любого вектора
(особая роль числового множителя 1).
Линейное пространство
![]() называется
n-мерным,
если в нем существует n
линейно независимых векторов, а любые
из
называется
n-мерным,
если в нем существует n
линейно независимых векторов, а любые
из
![]() векторов
уже являются зависимыми. Другими словами,
размерность
пространства
– это максимальное число содержащихся
в нем линейно независимых векторов.
Число n
называется размерностью пространства
и обозначается
векторов
уже являются зависимыми. Другими словами,
размерность
пространства
– это максимальное число содержащихся
в нем линейно независимых векторов.
Число n
называется размерностью пространства
и обозначается
![]() .
.
Совокупность n линейно независимых векторов n-мерного пространства называется базисом.
Скалярное произведение векторов и его свойства (длина вектора, угол между векторами)
Скалярным
произведение
![]() двух
векторов
и
называется число, равное произведению
длин этих векторов на косинус угла
двух
векторов
и
называется число, равное произведению
длин этих векторов на косинус угла
![]() между
ними:
между
ними:
![]()
Также эта формула имеет другой вид:
![]() ,
,
т. е. скалярное произведение двух векторов равно модулю одного из них, умноженному на проекцию другого на ось, сонаправленную с первым вектором.
Свойства:
1. Скалярное произведение обладает переместительным свойством: ab=ba
![]()

5. Если векторы а и b (ненулевые) взаимно перпендикулярны, то их скалярное произведение равно нулю, т. е. если a b, то ab=0. Справедливо и обратное утверждение: если ab=0 и а 0 b, то а b

Длина вектора.
![]()
Угол между векторами.
Определение угла φ между ненулевыми векторами а = (ax; ay; az) и b=( bх; bу; bг):

Отсюда следует условие перпендикулярности ненулевых векторов а и b:
![]()
Векторное произведение векторов и его свойства
Векторное
произведение векторов ![]() и
и ![]() -
вектор, обозначаемый
-
вектор, обозначаемый ![]()
![]() или
или ![]() для
которого:
для
которого:
 (
( -
угол между векторами
и
,
-
угол между векторами
и
,  );
);
тройка , , - правая.
Свойства векторного произведения.






если
 ,
то
,
то  равен
площади параллелограмма, построенного
на приведенных к общему началу
векторах
и
.
равен
площади параллелограмма, построенного
на приведенных к общему началу
векторах
и
.
Смешанное произведение векторов. Применение для проверки зависимости системы векторов
Определение:
![]()
Свойства смешанного произведения.



 -
компланарны.
-
компланарны.
Если V -
объем параллелепипеда, построенного
на приведенных к общему началу
векторах
,
и ![]() ,
то
,
то ![]() если
тройка
если
тройка ![]() правая,
и
правая,
и ![]() если
тройка левая.
если
тройка левая.
Различные формы уравнения плоскости
В трехмерном пространстве в декартовой системе координат любая плоскость описывается линейным уравнением Ax + By + Cz + D = 0, A2 + B2 + C2 ≠ 0.
Это уравнение называется общим уравнением плоскости.
Вектор N = (A, B, C) = A·i + B·j + C·k — нормальный вектор плосокости, он перпендикулярен любой прямой, принадлежащей плоскости.
Уравнение плоскости, проходящей через точку M0(x0,y0,z0) перпендикулярно вектору N = (A, B, C) имеет вид A(x −x0)+ B(y −y0) + C(z −z0) = 0. Это уравнение называют уравнением плоскости, проходящей через заданную точку с заданным нормальным вектором.
Виды уравнений плоскости в пространстве.
Если хотя бы одно из чисел А, В, С, D равно нулю, уравнение Ax + By + Cz + D = 0 называют неполным.
Виды неполных уравнений.
1) D = 0 – плоскость Ax + By + Cz = 0 проходит через начало координат.
2) А =
0 – n =
{0,B,C}![]() Ox,
следовательно, плоскость By + Cz + D =
0 параллельна оси Ох.
Ox,
следовательно, плоскость By + Cz + D =
0 параллельна оси Ох.
3) В = 0 – плоскость Ax + Cz +D = 0 параллельна оси Оу.
4) С = 0 – плоскость Ax + By + D = 0 параллельна оси Оz.
5) А = В = 0 – плоскость Cz + D = 0 параллельна координатной плоскости Оху (так как она параллельна осям Ох и Оу).
6) А = С = 0 – плоскость Ву + D = 0 параллельна координатной плоскости Охz.
7) B = C = 0 – плоскость Ax + D = 0 параллельна координатной плоскости Оуz.
8) А = D = 0 – плоскость By + Cz = 0 проходит через ось Ох.
9) B = D = 0 – плоскость Ах + Сz = 0 проходит через ось Оу.
10) C = D = 0 - плоскость Ax + By = 0 проходит через ось Oz.
11) A = B = D = 0 – уравнение Сz = 0 задает координатную плоскость Оху.
12) A = C = D = 0 – получаем Ву = 0 – уравнение координатной плоскости Охz.
13) B = C = D = 0 – плоскость Ах = 0 является координатной плоскостью Оуz.
Если же общее уравнение плоскости является полным (то есть ни один из коэффициентов не равен нулю), его можно привести к виду:
![]() называемому уравнением
плоскости в отрезках.
называемому уравнением
плоскости в отрезках.
Нормальное
уравнение плоскости
![]() где
где ![]() -
углы, образуемые нормальным вектором
плоскости с осями координат; p -
расстояние от начала координат до
плоскости.
-
углы, образуемые нормальным вектором
плоскости с осями координат; p -
расстояние от начала координат до
плоскости.
Приведение общего уравнения плоскости к нормальному виду:
![]()
Здесь ![]() -
нормирующий множитель плоскости, знак
которого выбирается противоположным
знакуD,
если
-
нормирующий множитель плоскости, знак
которого выбирается противоположным
знакуD,
если ![]() произвольно,
если D
= 0.
произвольно,
если D
= 0.
Уравнение плоскости по точке и нормальному вектору В векторном виде
![]()
В координатах
![]()
Уравнение плоскости по точке и двум неколлинеарным векторам В векторном виде
![]()
В координатах
![]()
Параметрические уравнения плоскости В векторном виде
![]()
В координатах
![]()
![]()
![]()
Уравнение
плоскости, проходящей через две
параллельные прямые ![]() и
и ![]()
![]()
Если прямые заданы соответственно уравнениями:
![]() и
и 
то уравнение плоскости есть
![]()
Уравнение
плоскости, проходящей через две
пересекающиеся прямые ![]() и
и ![]()
![]() или
или ![]()
Если ![]() ,
то уравнение плоскости есть
,
то уравнение плоскости есть

Типичные задачи для плоскости (уравнение плоскости через 3 точки, расстояние от точки до плоскости, геометрический смысл)
Уравнение плоскости по трем точкам В векторном виде
![]()
В координатах
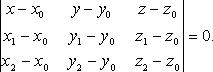
или

Расстояние
от точки до плоскости
![]()
![]()
Взаимное расположение плоскостей (когда перпендикулярны, параллельны, что такое угол между плоскостями)
Две плоскости в пространстве могут быть либо параллельны, в частном случае совпадать друг с другом, либо пересекаться. Взаимно перпендикулярные плоскости представляют собой частный случай пересекающихся плоскостей.
Две плоскости в пространстве называются параллельными, если они не пересекаются, в противном случаи они пересекаются.
Теорема 1: Если две пересекающиеся прямые одной плоскости соответственно параллельны двум прямым другой плоскости, то эти плоскости параллельны.
