
- •1. Вероятностные характеристики дискретных случайных величин
- •2. Вероятностные характеристики непрерывных случайных величин.
- •3. Формы представления законов распределения случайных величин.
- •4. Векторные случайные величины.
- •5. Типы случайных процессов.
- •6. Вероятностные характеристики случайных процессов.
- •7. Эргодическое свойство стационарных случайных процессов
- •8. Выбросы стационарных случайных процессов
- •9. Корреляционная функция и её основные свойства.
- •Свойства корреляционных функций
- •10. Экспериментальное определение корреляционных функций.
- •11. Спектральное разложение стационарных случайных процессов в непрерывный спектр дисперсий.
- •12. Свойства спектральной плотности.
- •13. Корреляционные функции и спектральные плотности типовых стационарных процессов.
- •14. Представление случайного процесса в виде канонического разложения. Интегральное каноническое представление случайного процесса. Полиномиальное представление случайного процесса.
- •Представление случайного процесса в виде канонического разложения Каноническое разложение корреляционной функции случайного процесса X(t):
- •Интегральное каноническое представление случайного процесса
- •Полиномиальное представление случайного процесса
- •15. Структура стохастической системы автоматического управления
- •16. Случайные процессы и возмущения в автоматических системах
- •17. Реакция динамической системы на случайное возмущение
- •18 Критерии точности системы
- •19 Характеристики выходных сигналов систем, заданных весовыми функциями
- •20 Корреляционный анализ систем, заданных дифференциальными уравнениями
- •21. Законы распределения выходных сигналов линейных систем (лс)
- •22. Определение установившихся систематических ошибок стационарных линейных систем (слс)
- •23. Определение установившейся дисперсии выходной переменной стационарной линейной системы (слс)
- •24. Критерии оптимальности автоматических систем.
- •25. Условие минимума среднеквадратичной ошибки.
- •26. Уравнение оптимальной линейной системы.
- •Определение весовой функции оптимальной линейной системы
- •Оптимальные системы, описываемые дифференциальными уравнениями
- •Дискретные случайные функции
- •30. Линейные операции над дискретными случайными функциями
- •Стационарные дискретные случайные процессы
- •32.Корреляционный анализ дискретных систем, заданных разностными уравнениями
- •33. Особенности вероятностного анализа нелинейных систем.
- •34. Линеаризация нелинейностей разложением в ряд.
- •35. Статистическая линеаризация нелинейностей.
- •36. Совместная гармоническая и статистическая линеаризация нелинейностей
- •37. Корреляционный анализ нелинейных систем, заданных дифференциальными уравнениями
- •38. Вероятностный анализ автоматических систем методом статистических испытаний
- •Марковские векторные процессы и последовательности
- •40. Уравнение Фоккера – Планка - Колмогорова
- •42. Анализ процесса срыва управления в автоматических системах
36. Совместная гармоническая и статистическая линеаризация нелинейностей
Входной сигнал нелинейного звена автоматической системы часто представляет собой сумму синусоидального сигнала определенной частоты и амплитуды и случайной функции x(t).
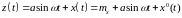 (1)
(1)
Если применить
только статическую линеаризацию, то
статические параметры
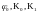 будут периодическими функциями. При
применении только гармонической
линеаризации гармонические коэффициенты
усиления будут случайными величинами.
Поэтому для уменьшения искажений
выходного сигнала в подобном случае
целесообразно применить совместную
статистическую и гармоническую
линеаризацию, т.е. заменить характеристику
нелинейного звена.
будут периодическими функциями. При
применении только гармонической
линеаризации гармонические коэффициенты
усиления будут случайными величинами.
Поэтому для уменьшения искажений
выходного сигнала в подобном случае
целесообразно применить совместную
статистическую и гармоническую
линеаризацию, т.е. заменить характеристику
нелинейного звена.
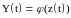 (2)
(2)
приближенной
зависимостью:
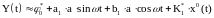 (3)
(3)
Зависимость (3)
линейна как относительно синусоидальной,
так и относительно случайной составляющих
входного сигнала. При этом, как и в
случае одной статистической линеаризации
и одной гармонической полезную
(систематическую) составляющую выходного
сигнала нелинейного звена можно
представить в виде:
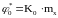 (4)
(4)
Величины
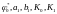 могут определяться различными способами
в зависимости от заданного критерия.
Если математическое ожидание
и дисперсия
могут определяться различными способами
в зависимости от заданного критерия.
Если математическое ожидание
и дисперсия
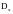 входного сигнала
входного сигнала
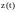 изменяются достаточно медленно, чтобы
считать их постоянными в пределах одного
периода синусоидальной части входного
сигнала, то целесообразно сначала
применить статистическую, а затем
гармоническую линеаризацию. В результате
статистической линеаризации получим:
изменяются достаточно медленно, чтобы
считать их постоянными в пределах одного
периода синусоидальной части входного
сигнала, то целесообразно сначала
применить статистическую, а затем
гармоническую линеаризацию. В результате
статистической линеаризации получим:
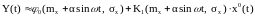 (5)
(5)
В данном случае
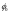 и
и
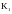 оказываются периодическими функциями
времени. Следовательно, к ним можно
применить метод гармонической
линеаризации. При этом нелинейная
функция
представляется рядом Фурье, в котором
оставляется только постоянная
(систематическая) составляющая и первая
гармоника.
оказываются периодическими функциями
времени. Следовательно, к ним можно
применить метод гармонической
линеаризации. При этом нелинейная
функция
представляется рядом Фурье, в котором
оставляется только постоянная
(систематическая) составляющая и первая
гармоника.
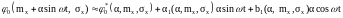 (6)
(6)
Величины
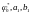 определяются по формулам гармонической
линеаризации
определяются по формулам гармонической
линеаризации
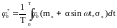 (7)
(7)
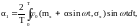 (8)
(8)
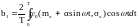 (9)
(9)
где
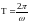 .
При разложении в ряд Фурье коэффициента
необходимо учесть только постоянную
составляющую, чтобы избежать появления
нелинейного члена.
.
При разложении в ряд Фурье коэффициента
необходимо учесть только постоянную
составляющую, чтобы избежать появления
нелинейного члена.
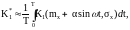 (10)
(10)
В случае нечетной характеристики нелинейного звена на основании (4)
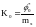
В некоторых случаях целесообразнее применять сначала гармоническую, а затем статистическую линеаризацию нелинейностей. Линеаризованные модели могут быть исследованы хорошо разработанными методами теории линейных систем.
37. Корреляционный анализ нелинейных систем, заданных дифференциальными уравнениями
Для корреляционного анализа нелинейных, в общем случае, нестационарных систем удобно применять метод моментов. При этом автоматическая система представляется векторно-матричным уравнением:
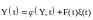 (1)
(1)
где
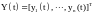 – вектор фазовых координат системы.
– вектор фазовых координат системы.
 –вектор нелинейных функций.
–вектор нелинейных функций.
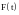 -
детерминированная матрица коэффициентов.
-
детерминированная матрица коэффициентов.
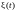 – вектор белых шумов с матрицей
интенсивностей
– вектор белых шумов с матрицей
интенсивностей
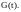 Каждая из
Каждая из
 составляющих вектора
составляющих вектора
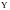 описывается скалярным уравнением:
описывается скалярным уравнением:
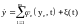 (2)
(2)
где
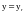 ,
,
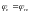 ,
,
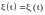 .
Индекс r
для упрощения записи опустим. Для каждой
из нелинейностей
.
Индекс r
для упрощения записи опустим. Для каждой
из нелинейностей
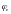 (если это существенная нелинейность)
можно применить статистическую
линеаризацию.
(если это существенная нелинейность)
можно применить статистическую
линеаризацию.
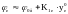 (3)
(3)
или для нечетных
нелинейностей
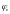 :
:
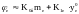 (4)
(4)
 – номер нелинейности,
входящей в
– номер нелинейности,
входящей в
 -e
уравнение компоненты
-e
уравнение компоненты
 .
С учетом (3), (4) уравнение (2) примет вид:
.
С учетом (3), (4) уравнение (2) примет вид:
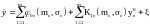 (5)
(5)
Применив к (5) операцию математического ожидания, получим
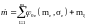 (6)
(6)
где
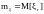 .
В отличие от рассмотренных ранее
уравнений моментов линейных систем
уравнения (6) не могут быть проинтегрированы
отдельно от уравнений для корреляционных
моментов, т.к. в (6) входят параметры
.
В отличие от рассмотренных ранее
уравнений моментов линейных систем
уравнения (6) не могут быть проинтегрированы
отдельно от уравнений для корреляционных
моментов, т.к. в (6) входят параметры
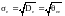 . Уравнение для компонент
векторно-матричного уравнения
корреляционных моментов имеют вид.
. Уравнение для компонент
векторно-матричного уравнения
корреляционных моментов имеют вид.
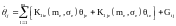 (7)
(7)
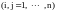
Уравнения (6), (7)
образуют замкнутую систему совместных
уравнений, определяющую неизвестные
функции времени
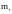 ,
,
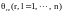 .
.
Порядок полной
системы уравнений моментов, подлежащей
интегрированию равен
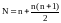 ,
,
где n – порядок исходной системы уравнений.
n |
1 |
2 |
… |
5 |
… |
10 |
… |
15 |
… |
N |
2 |
5 |
… |
20 |
… |
65 |
… |
135 |
… |
Как видно, порядок
системы уравнений моментов быстро
растет с увеличением порядка исходной
системы. Если применяется обычная
линеаризация дифференцируемых
нелинейностей (разложением в ряд), то
коэффициенты линеаризации не зависят
от корреляционных моментов
 .
.
В этом случае уравнения для математических ожиданий и корреляционных моментов могут интегрироваться раздельно.
Если автоматическая система стационарна и возмущения представляют собой стационарные случайные функции, то возможен установившийся режим ее функционирования.
Для установившегося
режима все производные равны нулю, т.е.
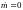 ,
,
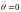 .
Уравнения превращаются в алгебраические
трансцендентные и могут быть решены
методом последовательных приближений.
.
Уравнения превращаются в алгебраические
трансцендентные и могут быть решены
методом последовательных приближений.
Метод статистической линеаризации может применяться успешно и для корреляционного анализа дискретных систем.
