
- •1. Вероятностные характеристики дискретных случайных величин
- •2. Вероятностные характеристики непрерывных случайных величин.
- •3. Формы представления законов распределения случайных величин.
- •4. Векторные случайные величины.
- •5. Типы случайных процессов.
- •6. Вероятностные характеристики случайных процессов.
- •7. Эргодическое свойство стационарных случайных процессов
- •8. Выбросы стационарных случайных процессов
- •9. Корреляционная функция и её основные свойства.
- •Свойства корреляционных функций
- •10. Экспериментальное определение корреляционных функций.
- •11. Спектральное разложение стационарных случайных процессов в непрерывный спектр дисперсий.
- •12. Свойства спектральной плотности.
- •13. Корреляционные функции и спектральные плотности типовых стационарных процессов.
- •14. Представление случайного процесса в виде канонического разложения. Интегральное каноническое представление случайного процесса. Полиномиальное представление случайного процесса.
- •Представление случайного процесса в виде канонического разложения Каноническое разложение корреляционной функции случайного процесса X(t):
- •Интегральное каноническое представление случайного процесса
- •Полиномиальное представление случайного процесса
- •15. Структура стохастической системы автоматического управления
- •16. Случайные процессы и возмущения в автоматических системах
- •17. Реакция динамической системы на случайное возмущение
- •18 Критерии точности системы
- •19 Характеристики выходных сигналов систем, заданных весовыми функциями
- •20 Корреляционный анализ систем, заданных дифференциальными уравнениями
- •21. Законы распределения выходных сигналов линейных систем (лс)
- •22. Определение установившихся систематических ошибок стационарных линейных систем (слс)
- •23. Определение установившейся дисперсии выходной переменной стационарной линейной системы (слс)
- •24. Критерии оптимальности автоматических систем.
- •25. Условие минимума среднеквадратичной ошибки.
- •26. Уравнение оптимальной линейной системы.
- •Определение весовой функции оптимальной линейной системы
- •Оптимальные системы, описываемые дифференциальными уравнениями
- •Дискретные случайные функции
- •30. Линейные операции над дискретными случайными функциями
- •Стационарные дискретные случайные процессы
- •32.Корреляционный анализ дискретных систем, заданных разностными уравнениями
- •33. Особенности вероятностного анализа нелинейных систем.
- •34. Линеаризация нелинейностей разложением в ряд.
- •35. Статистическая линеаризация нелинейностей.
- •36. Совместная гармоническая и статистическая линеаризация нелинейностей
- •37. Корреляционный анализ нелинейных систем, заданных дифференциальными уравнениями
- •38. Вероятностный анализ автоматических систем методом статистических испытаний
- •Марковские векторные процессы и последовательности
- •40. Уравнение Фоккера – Планка - Колмогорова
- •42. Анализ процесса срыва управления в автоматических системах
34. Линеаризация нелинейностей разложением в ряд.
Линеаризация нелинейностей состоит в приближенной замене нелинейной функциональной зависимости линеаризованной, связывающей входную и выходную переменные.
Если нелинейность описывается однозначной дифференцируемой функцией, то при случайном входном сигнале она может быть приближенно заменена рядом Тейлора относительно математического ожидания входной переменной с точностью до первой степени ее центрированного значения.
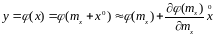 .
(1)
.
(1)
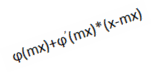
![]()
![]()
![]()
Здесь
 –
математическое ожидание случайной
входной переменной
–
математическое ожидание случайной
входной переменной
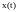 .
.
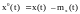 –
центрированная
случайная составляющая.
–
центрированная
случайная составляющая.
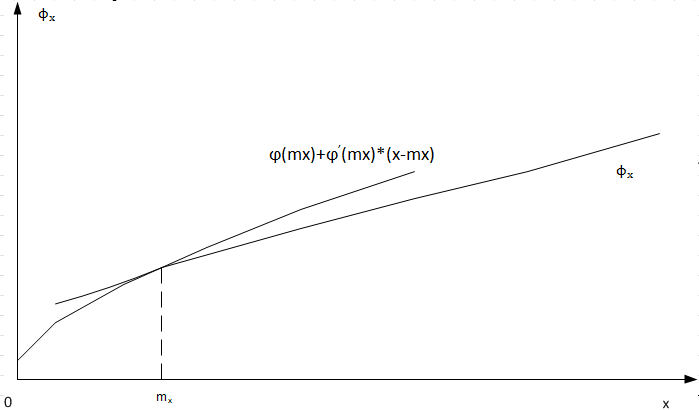
Приближенная
зависимость (1) линейна только относительно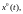 не линейна относительно
и равноценна
замене кривой
не линейна относительно
и равноценна
замене кривой
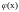 мгновенной касательной к ней в точке
мгновенной касательной к ней в точке
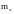 .
.
Степень точности зависимости (1) может быть оценена по средней статистической величине отбрасываемых членов разложения в ряд.
Для многомерной дифференцируемой нелинейности линеаризованная зависимость следующая.
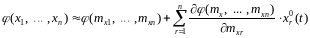 (2)
(2)
Пример 1
Нелинейность типа
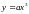 при
при
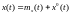 после
линеаризации разложением в ряд в
окрестности
после
линеаризации разложением в ряд в
окрестности
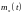 принимает вид
принимает вид

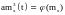 ,
,
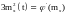
Пример 2
Нелинейность типа
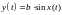 при
при
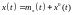 после линеаризации разложением в ряд
в окрестности
принимает вид
после линеаризации разложением в ряд
в окрестности
принимает вид

35. Статистическая линеаризация нелинейностей.
Для линеаризации
недифференцируемых
нелинейностей,
имеющих неоднозначные характеристики
или точки разрыва, удобно применять
т.н. статистическую линеаризацию,
разработанную И.Е.Казаковым. Применима
также, когда отклонения
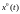 входной
переменной от ее математического
ожидания большие.
входной
переменной от ее математического
ожидания большие.
Статистическая линеаризация состоит в замене нелинейной зависимости линеаризованной, эквивалентной в вероятностном смысле.
Идея статистической линеаризации состоит в том, что линеаризованная зависимость должна с достаточной точностью определять полезный сигнал и уровень флуктуации на выходе нелинейного звена.
В результате
статистической линеаризации зависимость
между входной и выходной переменными
нелинейного звена
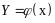 (1)
(1)
заменяется
приближенной зависимостью вида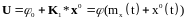 ,
,
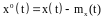 (2)
(2)
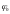 – выходной полезный
сигнал нелинейного звена, зависимость
которого от входного полезного сигнала
является статистической
характеристикой
нелинейного звена.
–
неслучайное.
– выходной полезный
сигнал нелинейного звена, зависимость
которого от входного полезного сигнала
является статистической
характеристикой
нелинейного звена.
–
неслучайное.
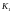 – статистический
коэффициент усиления нелинейного
звена по
случайной составляющей.
– статистический
коэффициент усиления нелинейного
звена по
случайной составляющей.
Первый способ
состоим в выполнении условия равенства
математических ожиданий и дисперсий
истинной и аппроксимирующей зависимостей,
т.е.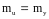 ;
;
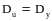 (4)
(4)
Вычислив известными способами математическое ожидание и дисперсию случайной величины U по выражению (2), получим
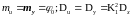 (5)
(5)
На основании формул (3), (5) имеем
 .
(6)
.
(6)
из второго выражения (5) имеем
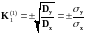 ,
(7) ,где
,
(7) ,где
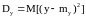 ;
;

 (8)
(8)
Знак коэффициента
определяется характером функции
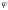 .
.
Если функция
возрастает
около точки
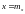 ,
,
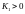 ,
иначе
,
иначе
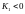 .
.
Условие (4) обеспечивает точный учет изменения нелинейным звеном полезного сигнала и уровня флуктуаций. При этом закон распределения выходного сигнала при статистической линеаризации в общем случае несколько искажается.
На основании этого способа возникает идея положить в основу метода статистической линеаризации другой принцип – минимум средней квадратической ошибки.
Второй способ
определения
параметров статистической линеаризации
состоит в том, что входящие в выражение
(2)
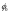 и
выбираются из условия
и
выбираются из условия
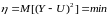 (
( -греческая
буква)
(9)
-греческая
буква)
(9)
Подставляя в (9)
выражение (2) (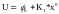 )
и используя известные свойства
математических ожиданий, получим
следующее условие
)
и используя известные свойства
математических ожиданий, получим
следующее условие
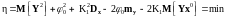 (10)
(10)
При известных
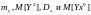 величина
величина
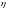 является функцией параметров
является функцией параметров
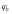 и
.
и
.
Приравнивая нулю
частные производные функции
по
и
,
получим уравнения 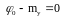 (11)
(11)
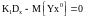 (12)
(12)
Экстремум
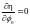 ,
,
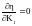 .
Уравнение (11) дает
полученную ранее для
формулу
.
Уравнение (11) дает
полученную ранее для
формулу
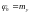 .
Из уравнения
(12) имеем
.
Из уравнения
(12) имеем
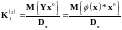 .
(13)
.
(13)
Для вычисления
величин
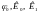 по полученным формулам необходимо знать
одномерную плотность вероятности
по полученным формулам необходимо знать
одномерную плотность вероятности
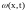 входной
переменной
входной
переменной
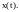
Тогда формулы (5), (6), (7), (13) имеют вид
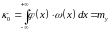 (14)
(14)
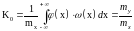 (15)
(15)
 (16)
(16)
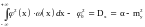
 (17)
(17)
где индексы вверху
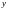 коэффициентов
указывают
способ линеаризации.
коэффициентов
указывают
способ линеаризации.
На практике
оказывается возможным в сложных
автоматических системах считать
гауссовой,
обозначив
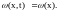 Закон
распределения выходной переменной тем
ближе к нормальному, чем инерционнее
система (больше ее постоянная времени).
Закон
распределения выходной переменной тем
ближе к нормальному, чем инерционнее
система (больше ее постоянная времени).
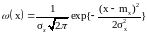 (18)
(18)
На основании (14),
(18) имеем
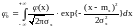 (19)
(19)
Если продифференцировать
(19) по
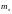 и сравнить с выражением (17), то получим
и сравнить с выражением (17), то получим
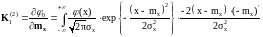 (20)
(20)
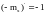 .В
практических расчетах можно использовать
.В
практических расчетах можно использовать
 или
или
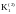 .
.
Для повышения точности расчетов при четных нелинейностях
 .
(21)
.
(21)
