32.Корреляционный анализ дискретных систем, заданных разностными уравнениями
Как и для непрерывных систем, здесь удобно использовать метод моментов. Для этого уравнение многомерной дискретной автоматической системы в векторно-матричной форме представляется в виде
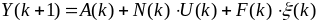; (5.32)
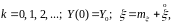
где Y(k) –
n-мерный
вектор;
–
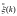дискретный гауссов центрированный
белый шум с матрицей дисперсий G(k);
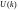– детерминированная
последовательность (управляющее
воздействие);
–
заданные (известные) матрицы коэффициентов.
Применяя операцию математического ожидания к правой и левой частям выражения (5.32), получаем разностное уравнение для вектора математического ожидания
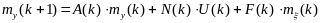. (5.33)
Вычитая почленно из уравнения (5.32) уравнение (5.33), получаем уравнение для центрированного вектора
. (5.34)
Выражение для
корреляционной матрицы процесса
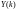имеет
вид
. (5.35)
Подставив в (5.35)
выражение (5.34) для
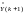и соответственно для
:
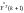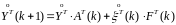(5.36)
и выполнив
соответствующие преобразования, получим
разностное уравнение для корреляционной
матрицы
:
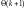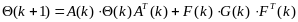. (5.37)
В уравнении (5.37)
учтено, что
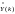и
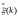независимы (некоррелированы).
Для установившегося режима в стационарной дискретной системе (если такой существует) из выражений (5.33) и (5.37) получаем следующую систему алгебраических уравнений:
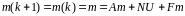, (5.38)
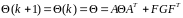. (5.39)
Из алгебраических
уравнений (5.38) и (5.39) определяются
установившиеся значения
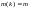и
.
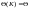Для определения
установившихся значени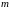й
и
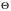могут использоваться рассмотренные
ранее методы, основанные на заданных
известных характеристиках входного
сигнала и заданной передаточной функции
системы (требуемой передаточной функции).
При этом необходимо учесть особенности и свойства передаточных функций дискретных систем.
33. Особенности вероятностного анализа нелинейных систем.
Нелинейной системой называется динамическая система, для которой не выполняется принцип суперпозиции.
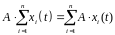A
– оператор системы.
Система является нелинейной при наличии в ней хотя бы одного элемента, для которого не выполняется принцип суперпозиции.
Динамические процессы в нелинейных системах существенно сложнее процессов, происходящих в линейных системах.
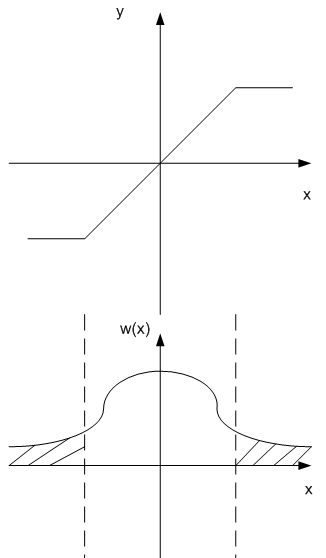
Нелинейные элементы систем в отличие от линейных, приобретают характер случайных процессов, изменяют их законы распределения.
Задачи анализа нелинейных динамических систем, находящихся под воздействием случайных возмущений, состоят в определении законов распределения или вероятностных численных характеристик всех или только выходных переменных; в исследовании зависимости этих характеристик от параметров системы, в определении точности преобразования полезных сигналов и т. д.
Для произвольных нелинейных систем не существует общего точного метода определения интересующих нас вероятностных характеристик.
Поэтому большое значение имеют приближенные методы решения задач анализа, которые основаны на линеаризации нелинейностей.
После линеаризации нелинейностей формально может быть применена линейная теория вероятностного анализа и прежде всего корреляционного.
При корреляционном анализе нелинейных систем применяются те же критерии точности, которые рассмотрены ранее для линейных систем, и определяются вероятностные моменты случайных процессов.
Основными вероятностными моментами здесь являются, как и ранее, математические ожидания и корреляционные функции.
Основные методы линеаризации стохастических систем следующие:
Линеаризация разложением в ряд применяется для т.н. «гладких» (дифференцируемых) нелинейностей.
Гармоническая линеаризация применяется при действии на нелинейные элементы гармонических (синусоидальных) сигналов.
Статистическая линеаризация применяется при случайных входных сигналах и т.н. «существенных» (недифференцируемых) нелинейностях.
Т.к. гармоническая линеаризация в основном применяется при анализе детерминированных процессов, то рассмотрим подробнее две другие.