Приведение объемных и поверхностных сил, а также начальных деформаций к эквивалентным узловым внешним силам.
При составлении
уравнений равновесия узлов всей
конструкции 
в методе перемещений предполагалось,
что все внешние нагрузки (силы, моменты)
приложены в узлах. Предположим теперь,
что помимо узловых внешних сил на
рассматриваемый конечный элемент
действуют объемные силы интенсивностью
и поверхностные силы интенсивностью
.
Кроме того, конечный элемент имеет
начальные деформации 
,
которые могут быть вызваны, например,
температурным воздействием.
Для определения
эквивалентных узловых усилий поступим
следующим образом. Дадим перемещениям
элементы 
малые вариации 
и найдем работу по объему и поверхности
конечного элемента указанных выше сил
на этих вариациях:
(69)
V-объем конечного элемента, S-поверхность конечного элемента.
На основании
зависимостей 
и закона Гука 
будем иметь, что
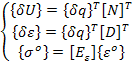(70)
Где 
- зависят от координат по объему конечного
элемента.
Подставляя (70) в (69) получим:
(71)
В полученном
выражении коэффициенты, стоящие при
вариациях узловых (обобщенных) перемещениях
,
и будут представлять вектора искомых
узловых (обобщенных) усилий:
-от
действия объемных сил интенсивностью
(72)
-
от действия поверхностных сил,
интенсивностью
(73)
-
нормаль к поверхности, задающей ее
ориентацию.
-
от действия начальных деформаций
.
(74)
Таким образом,
если на отдельные к
элементы действуют внешние объемные и
поверхностные силы и имеется начальное
деформированное состояние, то при
составлении уравнения равновесия i-ого
узла вместо узлового усилия
следует ввести величину:
,
(75)
где суммирование производиться по всем к элементам, сходящимся в i-ом узле.
Необходимо
отметить, что при учете начальных
деформаций компоненты напряжения
в каждом из элементов будут определяться
с помощью зависимости:
или если принимать во внимание например (18), то
.
Приведенный вывод выражений (72), (73) и (74) для эквивалентных узловых усилий был основан на равенстве работ, совершаемых действующей на элементы внешней нагрузкой и эквивалентными ей узловыми усилиями на соответствующих возможных перемещениях, т.е. обобщенным перемещением элементов были найдены обобщенные усилия.
Точность замены внешних распределенных нагрузок эквивалентными узловыми усилиями во многом зависит от того, насколько удачно выбрано аппроксимирующее выражение для перемещений , которое отображает действительный характер перемещений по объему рассматриваемого КЭ.
Колебания объемных тел.
Любая упругая конструкция, подверженная действию статических нагрузок, может быть проанализирована с помощью матричного метода конечных элементов (22).
Каждое i-ое уравнение матричного уравнения (22) выражает условие равновесия дискретной системы по направлению i-ого перемещения, т.е. сумма реакций в этом направлении от всех сходящихся в данном узле элементов равна узловой внешней силе в этом направлении. Это условие остается справедливым для любой упругой системы. Причем физическая природа происхождения внешних сил может быть любой (инерционные, аэро - гидродинамические, электромагнитные, оптические и т. д.)
Согласно принципу
Даламбера задача динамики упругой
системы может быть сведена к соответствующей
задаче статики при условии включения
инерционных сил (равных произведению
масс на их ускорения, взятых с обратным
знаком) в разряд внешних нагрузок. Тогда
матричное уравнение (22) при действии
переменных во времени внешних узловых
усилий
принимает вид:
(77)
Каждый из КЭ под
действием внутренних и внешних сил (
включая силы инерции и узловые реакции
взаимодействия со смежными элементами)
находится в равновесии. Следовательно,
для определения его неизвестных узловых
перемещений
можно
воспользоваться уравнениями Лагранжа
2-ого рода:
,
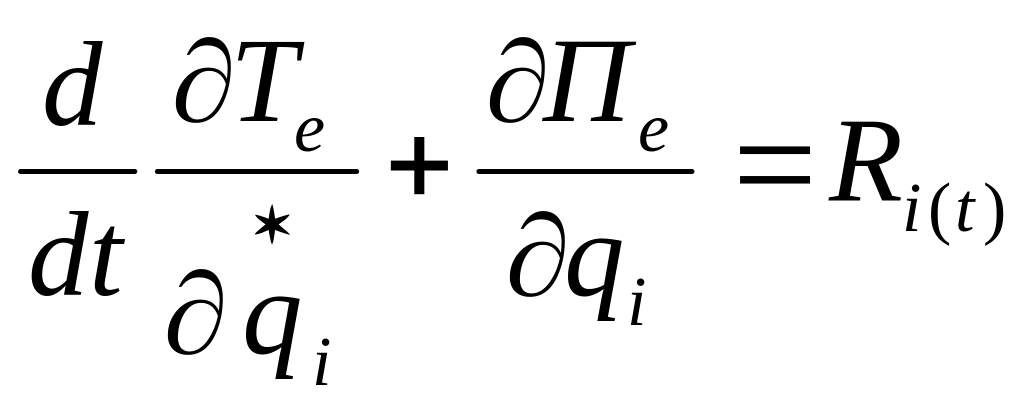(78)
Определяем напряжения τz в горизонтальных сечениях:
а) горизонтальные сечения строятся на основе вертикальных;
По найденным значениям τz строим эпюры касательных напряжений, учитывая, что в левой половине пластины во всех симметричных точках τz будет иметь те же значения, что и в правой половине, но противоположного знака.