Вариационные и векторные методы решения задач механики.

Классификация задач механики:

- по геометрии деформируемых тел:

а) трехмерные – все три размера соизмеримы (требуют использования полной системы уравнений теории упругости или пластичности - SOLID)

б) пластины и оболочки – два размера соизмеримы, а третий много меньше. Для них разработана специальная теория пластин и оболочек (Shell)

в) тонкостенные стержни – длина много больше размеров конечного сечения, которое, в свою очередь, много больше толщины элементов стержня. Для них разработана теория тонкостенных стержней Власова-Уманского (BEAM 3D)

г) брус (балка) – длина много больше поперечных размеров. Для них применяется элементарная теория деформированных балок (BEAM 2D, 3D)

- по признаку линейности или нелинейности:

т.е. искомые функции входят в уравнение линейно или нелинейно.

Различают нелинейности:

а) геометрическую, которая обусловлена нелинейной связью тензора деформаций ε_ij и проекций перемещений U_i(x₁, x₂, x₃) точек тела. Если производные , то нелинейные члены уравнений связи можно отбросить и считать задачу геометрически линейной, т.е. использовать соотношения Коши:

ε_ii = ; ε_ij = ( i ≠ j) i, j =1, 2, 3;

б)физическую, которая обусловлена нелинейной связью тензоров напряжений σ_ij и деформаций ε_ij. Нелинейная связь имеет место для физически нелинейных материалов или в упруго-пластической области активного деформирования тела. Закон Гука определяет линейную связь между σ_ij и ε_ij в теле.

- по дополнительным условиям:

а) задачи с начальными условиями (задачи Коши)

б) задачи с краевыми условиями. Краевая задача называется однородной, если правые части диф. уравнений и краевых условий равны нулю (например, устойчивость стержня на жестких опорах)

по признаку стационарности и нестационарности:

если функции, входящие в уравнения, и искомое решение, кроме ординат, содержат время, то такие задачи нестационарными;

если время в уравнение и решение явно не входит, то задача относится к классу стационарных.

Формы представления задач механики.

1. С помощью понятий векторной механики.

Векторная механика опирается на законы Ньютона и использует понятия вектора силы и импульса силы, на основе принципа статики или кинетостатики в МСС строятся дифференциальные уравнения равновесия и движения отдельных элементов внутри и на поверхности тела. В тензорной форме дифференциальные уравнения движения внутри тела и граничные условия имеют вид:

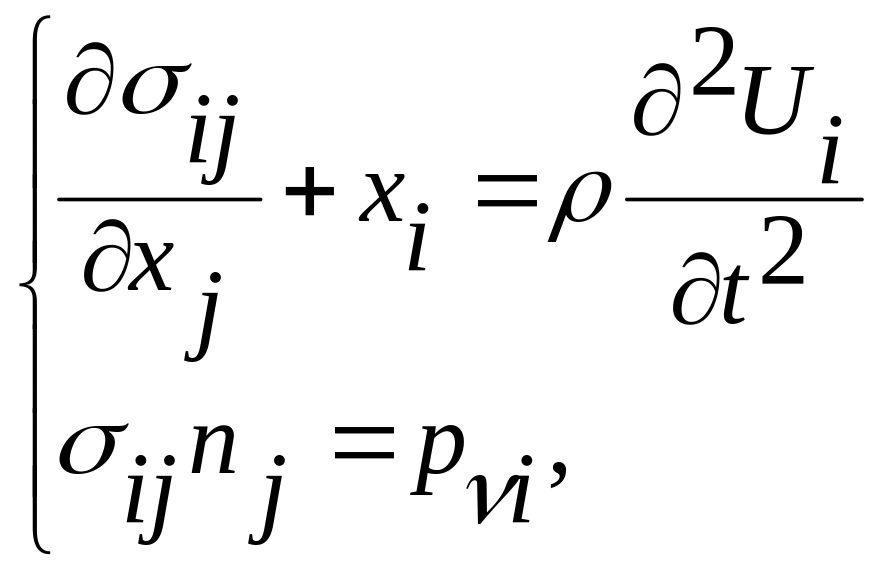
(2)

Где , - проекции векторов единичных объемных и поверхностных сил;

- плотность тела.

2. Описание задач с помощью понятий аналитической механики.

Аналитическая механика строится на принципе наименьшего действия и использует скалярные понятия потенциальной и кинетической энергий тела в целом. Принцип наименьшего действия определяется функциональным уравнением:

Ф=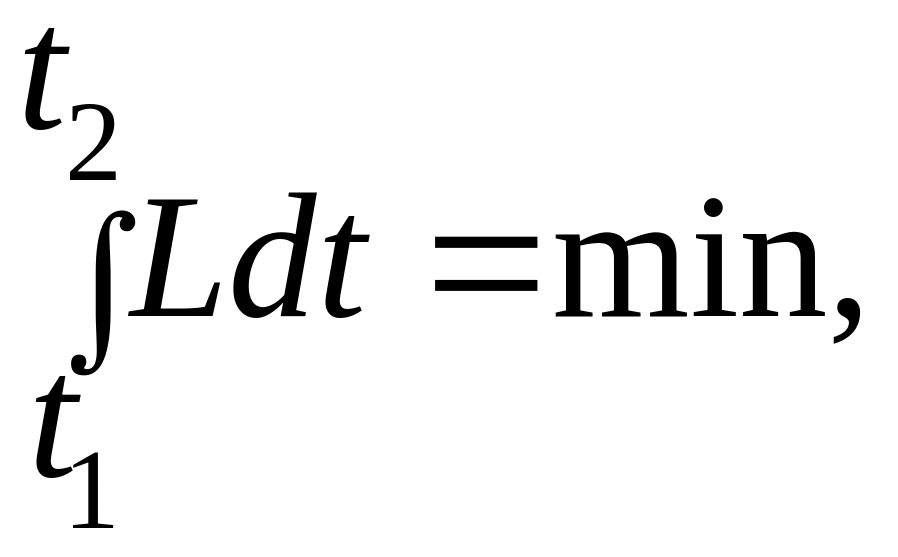 (3)

Где L=U-K – функция Лагранжа;

U,K – потенциальная и кинетическая энергии системы (тело вместе с воздействующими на него другими телами).

Согласно принципу наименьшего действия истинным напряженно-деформированным состоянием тела является то, при котором выполняется условие (3). Задача о минимизации функционала Ф решается методами вариационного исчисления. Согласно вариационному исчислению условие (3) выполняется, если первая вариация функционала равна нулю:

Ф=0 (4)

Векторная и аналитическая механики дают два различных математических описания и решения одной и той же задачи, но приводят к одному результату.

Различие состоит в следующем:

А) Векторная механика приводит к дифференциальным, а аналитическая – к функциональным уравнениям;

Б) В векторной механике внешние воздействия характеризуются силами, а в аналитической – работой, совершаемой этими силами на вариациях перемещений тела;

В) Векторная механика выделяет один малый элемент тела и рассматривает его изолированно от остальных элементов, а аналитическая – рассматривает искомое тело в целом с воздействующими на него другими телами;

Г) В векторной механике силы вычисляются отдельно для каждого элемента тела, а в аналитической – силы, действующие на каждый элемент тела, определяются из одной скалярной функции (функционала), которая содержит в себе необходимую информацию о действующих на тело силах;

Д) В векторной механике используются обычно декартовы или криволинейные координаты, а в аналитической – в качестве системы координат может быть выбрана любая совокупность параметров, однозначно характеризующих положение системы (обобщенные координаты).

Все уравнения векторной механики (уравнения равновесия и сплошности) могут быть получены из функциональных уравнений аналитической механики. Применение аналитической механики наиболее эффективно в консервативных задачах (когда силы имеют силовую функцию).

Понятие о вариациях функции и функционала

Под вариацией функции δy понимают бесконечно малое независимое изменение функции при неизменном значении её аргументов.

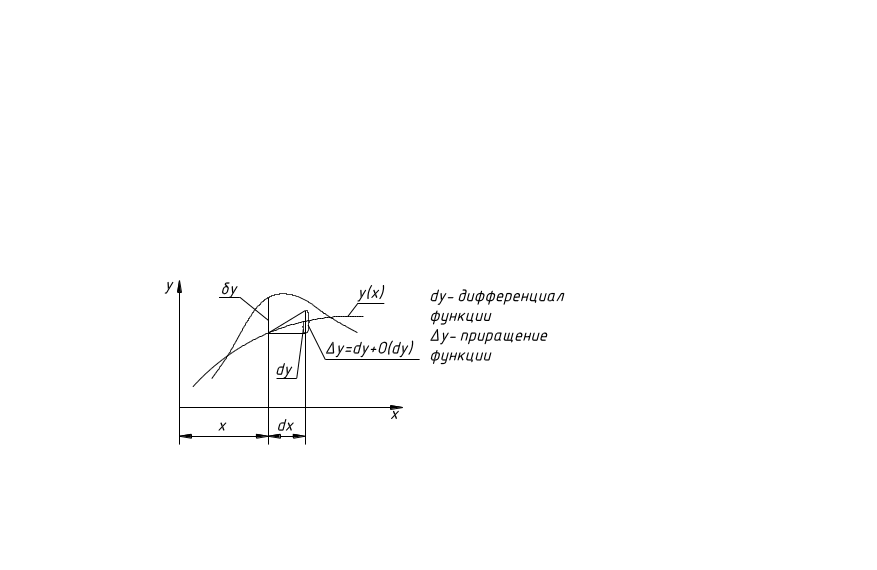Пусть задан функционал (функция от функций)

Ф=Ф[x, y(x), z(x)],

в котором y(x), z(x) ― функции.

Дадим вариации функциям и вычислим новое значение функционала

Ф[x, y+δy, z+δz], используя разложение в ряд Тейлора нового значения функционала по вариациям функций:

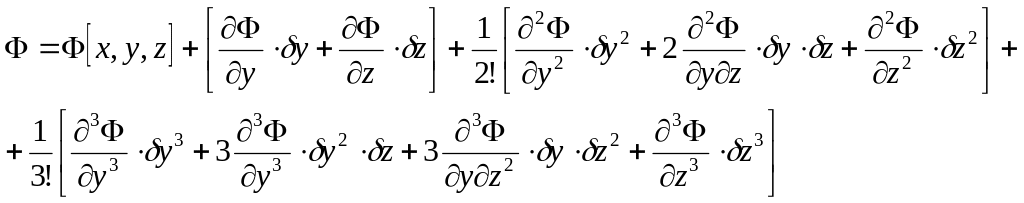(5)

Второе, третье, четвертое и т.д. слагаемые в квадратных скобках обозначают δФ,

δ²Ф, δ³Ф ― первая, вторая, третья вариации функционала.

Тогда вместо ряда (5) можно записать:

(6)

Рассмотрим случай однородного квадратичного функционала от двух функций:

Вычислим значение данного функционала при вариациях функций δy и δz

(7)

Из (7) следует, что

(8)

Сравнивая (6) и (8), находим, что квадратичный функционал имеет

(9)

Примером однородного квадратичного функционала от шести функций является упругий потенциал

(10)

где K ― модуль объемной упругости; G ― модуль сдвига,

; ; ;

e является положительно-определенным, т.к. при любых ε_ij≠0 больше нуля. Из выражений (9) и (10) следует, что δ²e>0.

Вариационные принципы аналитической механики.

1. Принцип минимальности потенциальной энергии системы или деформированного состояния тела (принцип Эйлера-Лагранжа). Этот принцип следует из принципа возможных перемещений:

2. Если абсолютно твердое тело находится в равновесии под действием заданных сил, то любые допускаемые связями малые отклонения тела (вариации перемещения тела) от состояния равновесия совершаются без затраты суммарной работы воздействующих сил.

δu₂

P₁

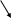
P₂ δu₁

; (11)

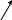Состояние 1

P_n δu_n

В МСС допускаемыми отклонениями (вариациями) называют такие вариации перемещений тела, которые удовлетворяют заданным кинематическим условиям задачи и условиям неразрывности деформаций. Различают работу внешних А^вн и внутренних А^вт сил. Если А^вн>0, А^вт<0. Величина П=-А^вт в МСС называется потенциальной энергией деформации тела.

Получим уравнение принципа Эйлера-Лагранжа для деформируемого твердого тела, используя выражение (11).

Пусть деформируемое тело находится в равновесии под действием объемных сил Х_i и поверхностных сил P_νi (i=1, 2, 3).

Напряженно-деформированное состояние тела определяется тензорами σ_ij, ε_ij, а проекции перемещений - функциями u_i (х₁, х₂, х₃), т. е. выполняются условия равновесия (2) при ρ Ξ0. Дадим перемещениям независимые, допустимые связями тела, вариации δu_i (i=1, 2, 3). При этом нагрузку на тело и тензор σ_ij полагаем неизменными. На данных вариациях внешние и внутренние силы совершают работу

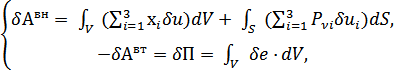(12)

где V, S – объем и поверхность тела;

е – удельная потенциальная энергия деформации, определяемая для идеально-упругого тела по формуле (10);

Подставляя (12) в (11), получим:

δU = 0, (13)

где U – потенциальная энергия системы

U = П-А^вн (14)

Уравнение (13) представляет собой первое вариационное уравнение аналитической механики и выражает принцип Эйлера-Лагранжа, согласно которому для тела, находящегося в равновесии, имеет место минимум потенциальной энергии системы. Действительно, учитывая, что δ²е>0, δ²А^вн=0, имеем δ²U>0 при δU_i≠0.

Из уравнения (13), как следствие, можно получить уравнения равновесия вместе с граничными условиями.

Пример: Используя принцип Эйлера-Лагранжа получить уравнение равновесия и граничные условия для балки постоянного сечения на жестких опорах.

Д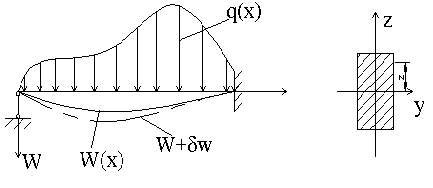 ля балки упругий потенциал

;

( )→ → где Е – модуль Юнга, W – прогиб балки, Z – расстояние от нейтральной линии балки по высоте сечения.

Запишем принцип Э – Д:

В результате уравнение (13) запишется так:

(15)

Учитывая свойства вариации и производной от вариации:

- производная от вариации равна вариации от производной;

- интеграл от вариации равен вариации от интеграла;

- вариация произведения функций.

Выражение (15) можно привести к виду:

(16)

Э то уравнение будет выполняться при любых значениях x, если ;

При x=0

При x=l (17)

Таким образом, уравнение изогнутой оси балки и граничные условия (17) являются следствием вариационного уравнения (15).

2. Принцип минимальности напряженного состояния (принцип Кастильяно)

Пусть тело находится в равновесии под действием объемных и поверхностных сил, т. е. выполняются дифференциальные уравнения равновесия вместе с граничными условиями. При этом деформация тела определяется перемещениями При тех же объемных силах дадим вариацию тензору напряжений , причем эта вариация должна удовлетворять условиям равновесия тела, т. е. должны выполняться условия . Это приводит к необходимости дать вариацию поверхностным силам, чтобы выполнялись условия .

В этом случае на основе уравнений (11) (принцип возможных перемещений)

, (18)

где

U₁-дополнительная потенциальная энергия системы;

П₁-дополнительная потенциальная энергия деформации тела.

(18)

Выражение (18) представляет собой принцип Кастильяно: из напряженных состояний тела действительным является то, при котором дополнительная потенциальная энергия системы минимальна.

Для физически нелинейных тел П₁>П.

В случае физически линейного тела П₁=П.

Из уравнения (18) можно, как следствие, получить условия совместности Сен-Венана.

Пример: Получить условие совместности при изгибе балки постоянного сечения, используя принцип Кастильяно.

Дадим такие вариации напряжениям в балке δσ и внешней нагрузке δq, чтобы выполнялись условия равновесия

(19)

При этом согласно условию (18)

(20)

Подставив во второе слагаемое выражение (19), после тождественных преобразований получим

или

Отсюда следует условие связи деформации с прогибами пи изгибе балки (гипотеза плоских сечений)

3. Принцип минимальности динамически деформированного состояния тела (принцип Гамильтона)

В случае динамического деформирования в состав объемных сил войдут еще силы инерции проекции которых равны . С учетом этих мил первое вариационное уравнение (13) записывается так

(21)

Проинтегрируем (21) по времени на интервале (t₁, t₂), полагая, что (i=1,2,3) для t= t₁ и t= t₂.

В результате

(22)

Преобразуем члены второго интеграла, используя формулу интегрирования по частям в определенном интеграле, согласно которой

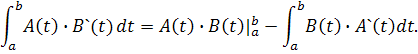
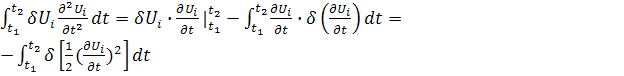(23)

Здесь учтено, что первое слагаемое равно нулю, т.к.

Тогда уравнение (22) запишется как

(24)

Где K= -кинетическая энергия.

Из уравнения (24) следует уравнение (4), определяющее принцип Гамильтона: на участке действительного динамического деформирования тела (t₁, t₂) вариация интеграла от функции Лагранжа равна нулю:

 dt=0 (25)

Это говорит о том, что на участке действительного динамического деформирования тела (t₁, t₂) тело деформируется таким образом, чтобы интеграл:

Ф= dt

имел наименьшее возможное значение.

Из уравнения (25) можно вывести уравнение равновесия (2).

3. Принцип Дирихле.

Сформулированные выше принципы определяют условия равновесия тела, оставляя вопрос о теле равновесия:

1. если U=0 и ²U>0 – равновесие устойчивое;

2. если U=0 и ²U<0 – равновесие неустойчивое;

3. если U=0 и ²U=0 – равновесие безразличное.

Вариационные методы решения задач.

Различают прямые и непрямые методы решения задач строительной механики на основе изложенных выше принципов. Можно из вариационных принципов Эйлера-Лагранжа или Гамильтона вначале получить искомые дифференциальные уравнения конкретной задачи вместе с граничными условиями, а затем проинтегрировать данные уравнения и получить искомое решение. Это непрямой метод. Но достоинство вариационных принципов не в возможности нахождения дифференциальных уравнений задачи (эти уравнения можно получить и с помощью векторной механики), а в том, что уравнения (4) Ф=0, (13) U=0, (18) U₁=0 допускают их прямое решение на основе аппроксимации деформированного или напряженного состояния тела. Это прямой метод.

Рассмотрим далее только прямые методы.

1. Метод Ритца. Пусть задан функционал U, зависящий от одной функции и ее производных:

U= [W(x),W’(x),W’’(x),…,W⁽ⁿ⁾(x)]dx (26)

Требуется определить функцию W(x). Представим эту функцию в виде ряда

W(x)= W_i(x), (27)

где a_i – некоторые неопределенные пока параметры,

W(x) – линейно-независимые аппроксимирующие функции, удовлетворяющие как минимум кинематическим условиям задачи (подлежат выбору).

Дадим функции W вариацию W≠0. С учетом (27) и определения вариации функции имеем:

W= , (28)

где a_i – произвольные независимые вариации параметров a_i.

На основании (13) U=0 и определения первой вариации функционала:

U= (29)

Так как a_i – произвольные независимые вариации, уравнение (29) будет выполняться при условиях

(i=1,2,…,n) (30)

Система алгебраических уравнений (30) относительно а_i будет линейной в случае квадратичного функционала (26), который имеет место при упругом деформировании.

Определив из решения системы линейных алгебраических уравнений параметры a_i, найдем искомое решение, а именно функцию (27).

Пример: Определить функцию прогиба балки переменного сечения на упругом основании и нагруженной сосредоточенными силами и моментами и распределенной нагрузкой q(x).

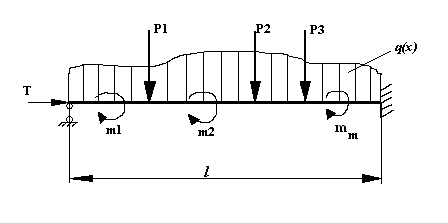
Для данного случая функционалом является потенциальная энергия системы, которая определяется выражением

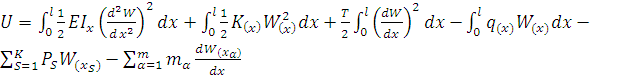(31)

Подставим (27) в (31) и запишем i-тое уравнение :

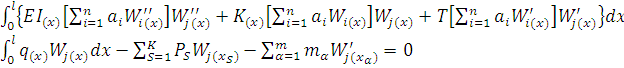
(j=1,2,…,n) (32)

Обозначим

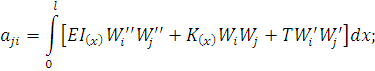
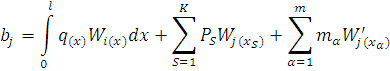
Тогда система (32) может быть записана в матричном виде

, (33)

где

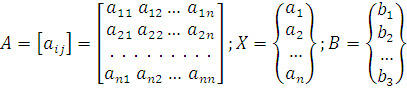
Система (33) решается на ЭВМ с помощью стандартной программы. Искомый вектор Х определяет решение задачи (27).

2. Метод Бубнова-Галеркина. Пусть задано дифференциальное уравнение задачи

(34)

с граничными условиями

(i=1,2,3, …, n) (35)

где L – дифференциальный оператор;

- заданные числа.

Дифференциальные уравнения МСС выражают условия равенства нулю равнодействующих сил, приложенных к бесконечно малому элементу внутри деформированного тела. Согласно принципа возможных перемещений работа равнодействующих на вариациях соответствующих перемещений

должна быть равна нулю для тела в целом:

(36)

Искомое решение уравнения (36) будем искать в виде (27),т.е.

,

где - линейно-независимые аппроксимирующие функции, удовлетворяющие всем граничным условиям задачи, т.к. формула (36) выражает условие равенства нулю работы лишь для внутренней области тела.

Подставляя в (36) (27) и (28),получим:

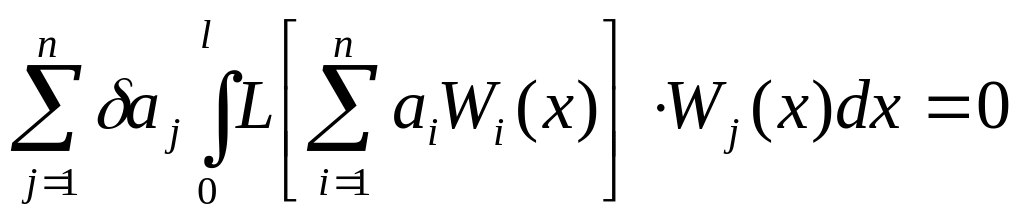(37)

В силу независимости уравнение (37) будет выполняться при условиях

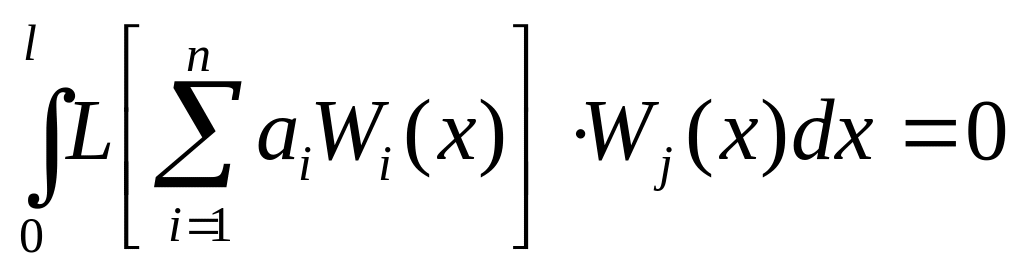, ( j = 1, 2, 3,…,n) (38)

представляющих собой систему алгебраических уравнений относительно . В случае линейного уравнения (34) будет линейной и система (38). Метод Бубнова - Галеркина применим как к консервативным, так и к неконсервативным задачам механики. (Метод Ритца применим только к консервативным задачам механики.)

В вычислительном плане метод Бубнова- Галеркина предпочтительнее метода Ритца, т.к. требует меньшего объема вычислений.

Пример: Определить критические силы и формы потери устойчивости.

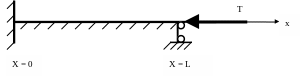
Дифференциальное уравнение равновесия имеет вид

Используя метод Бубнова- Галеркина, получим систему:

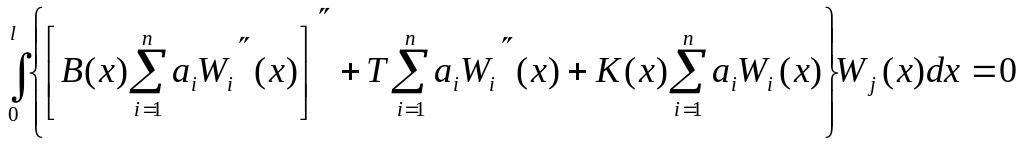
( j =1, 2, 3,…n )

Обозначим

В результате получаем однородное матричное уравнение

(39)

где , - квадратные матрицы;

- вектор неизвестных

Уравнение (39) можно переписать как

, (40)

где ; -единичная матрица;

Таким образом,задача об устойчивости балки сведена с помощью данного метода к задаче о собственных значениях (T_i) и вектора (X_i) характеристической матрицы С, которая решается с помощью стандартной программы. Формы потери устойчивости балки определяются выражениями

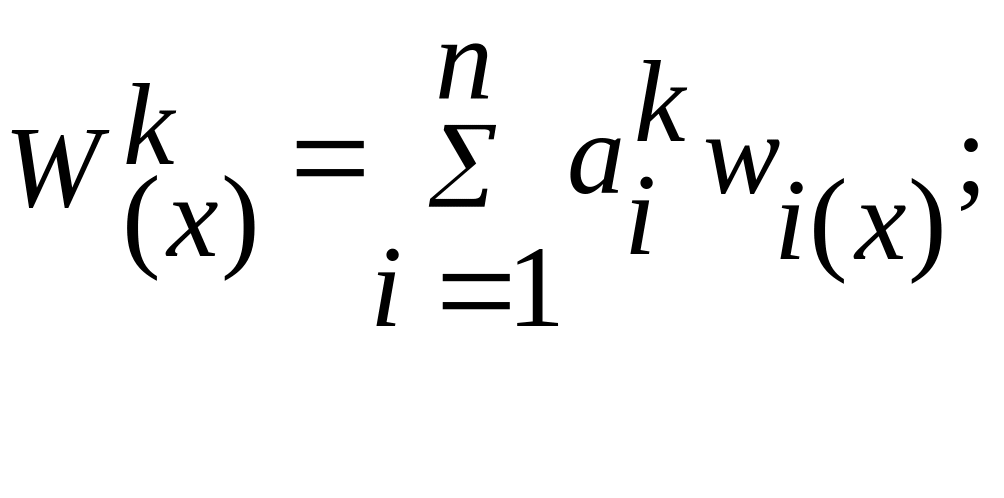(k=1,2,3,…,n)

3. Метод Власова-Канторовича. Разработан для приближенного интегрирования диф. уравнений в частных производных

(41)

Это уравнение можно проинтегрировать (т.е. найти функцию W(x,y)) методом Бубнова-Галеркина, если задаться решением в форме

или

Где W_i(x,y), X_i(x), Y_i(y) - заданные аппроксимирующие функции удовлетворяющие всем граничным условиям. Однако такие функции трудно подобрать и точность решения невысокая.

В методе Власова-Канторовича решение ищется в формуле

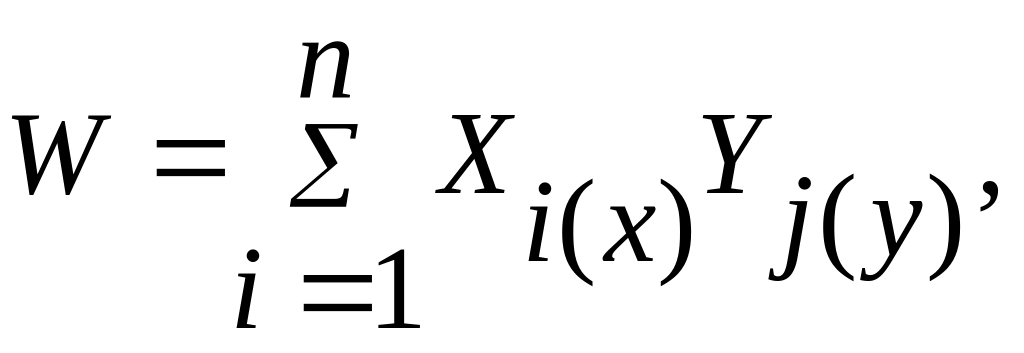(42)

Где одна из функций задается и должна удовлетворять всем граничным условиям на концах области определения этой функции, а другая находится с помощью интегрирования обыкновенного дифференциального уравнения, к которому приводится (41).

Подставим ряд (42) в (41) и используем метод Бубкова-Галеркина, полагая, что задана аппроксимирующая функция Y_i(y):

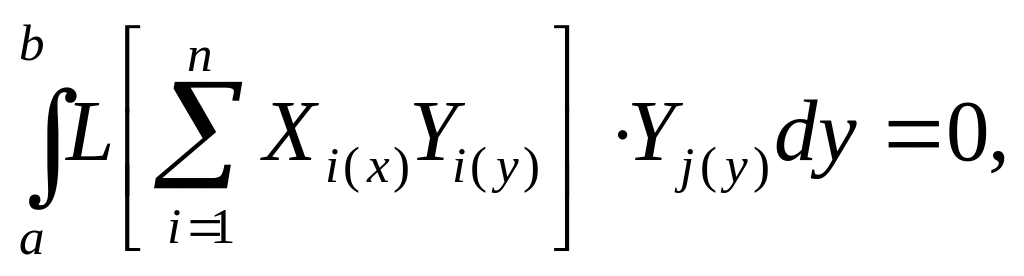(j=1,2,…,n) (43)

После интегрирования (43) вместо (41) получим систему обыкновенных дифференциальных уравнений относительно неизвестных функций X_i(x). Для того, чтобы искомая система ОДУ разделилась на n независимых дифференциальных уравнений в качестве Y_i(y) выбирают ортогональные функции, т.е.

Пример: Определить функцию прогиба жесткой пластины, загруженной равномерно-распределенной нагрузкой. Дифференциальное уравнение изгиба пластины

где цилиндрическая жесткость пластинки,

h-толщина пластины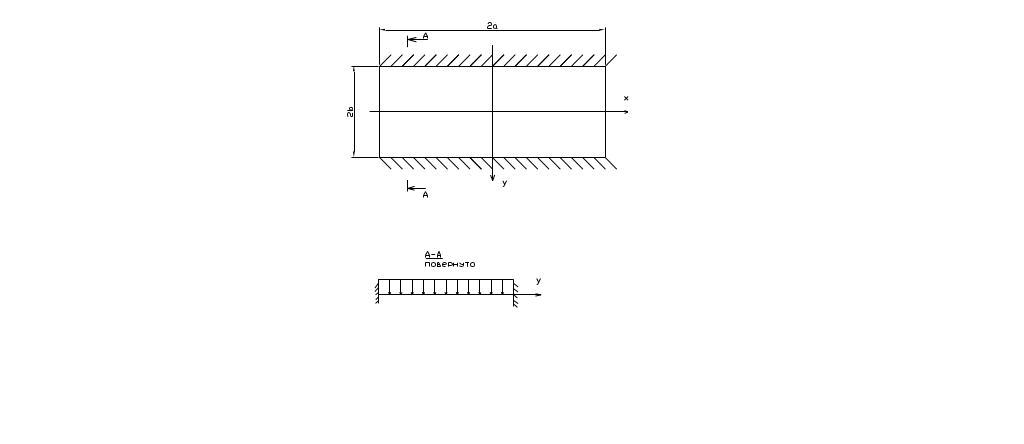

или

Решение ищем в форме

Где удовлетворяет всем граничным условиям при y=±b.

В этом случае (43) запишется как

(44)

После подстановки Y(y) в (44) и интегрирования получим обыкновенное дифференциальное уравнение

Это уравнение интегрируется аналитически, постоянные интегрирования определяются из граничных условий при x=±a/ Решение,полученное данным методом является более точным чем на основе метода Бубнова-Галеркина.

Выбор аппроксимирующих функций.

Рассмотренные выше методы дают приближенное решение задач, сходящееся к точному по мере увеличения числа членов ряда в (27). Аппроксимирующие функции должны удовлетворять следующим условиям:

1. Удовлетворять кинематическим условиям задачи (в том числе, уравнениям сплошности);

2. Качественно правильно отражать решение;

3. Быть линейно-независимыми (в противном случае, матрица (33) будет вырожденной);

4. Удовлетворять по возможности большему числу граничных условий.

Для стержневых систем аппроксимирующие функции выбирают в виде:

1. Полиномов различных степеней.

.

При построении выражений для данной функции, число параметров в полиноме, должно быть на единицу больше числа используемых граничных условий. Для консольной балки имеется выражение , удовлетворяющее всем граничным условиям:

. (50)

(50) – функция Дункана.

2. Тригонометрических функций.

Для свободно опертой балки можно использовать выражение:

;

Для симметричной, жестко-заделанной балки (нагрузка симметричны

относительно середины пролета):

.

3. Форм потери устойчивости или собственных колебаний балок постоянного сечения при расчете изгиба балок и арок переменного сечения.

Пример. Разработать алгоритм решения задачи о собственных колебаниях консольной балки переменного сечения.

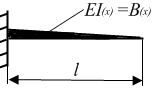
Решение. Используем принцип Гамильтона (25):

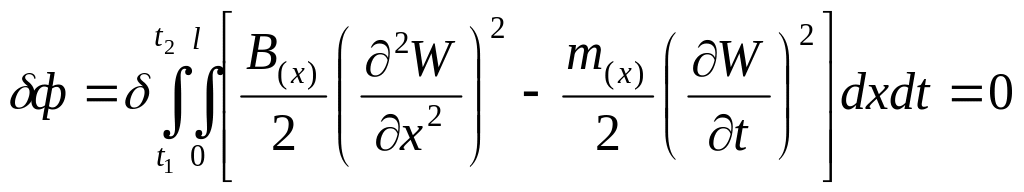(51)

В качестве интервала ( ) примем период собственных колебаний , где - круговая частота собственных колебаний балки.

Прогиб будем искать в виде:

, (52)

Где - функция Дункана (50).

Подставим (52) в (51) и проинтегрируем по времени.

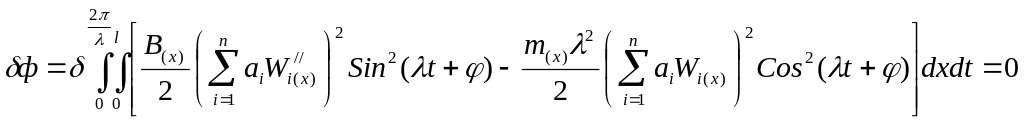Учитывая, что

и аналогично: .

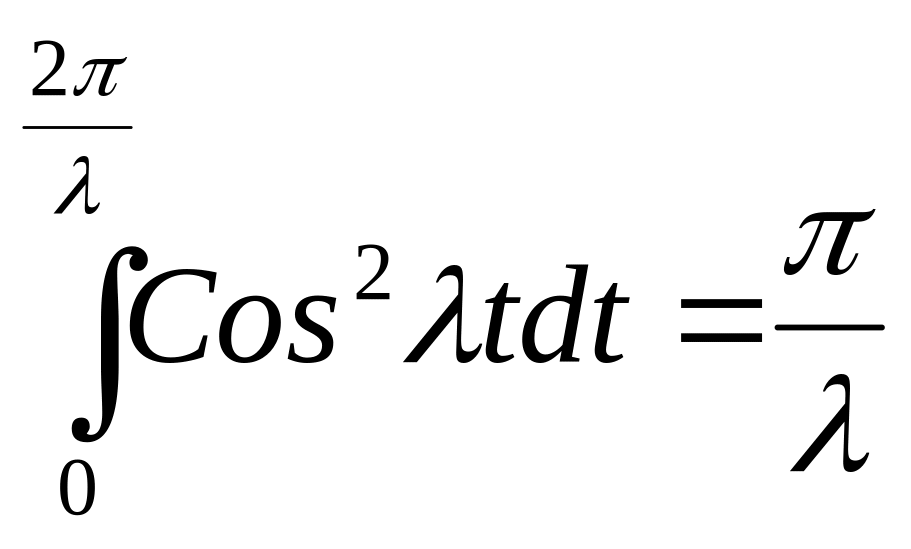В результате получим:

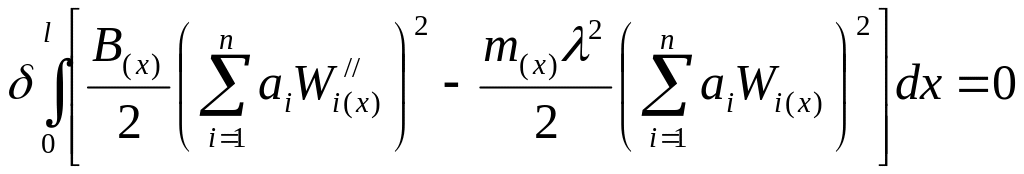. (53)

Согласно методу Ритца (дифференцируем, как сложную функцию) или

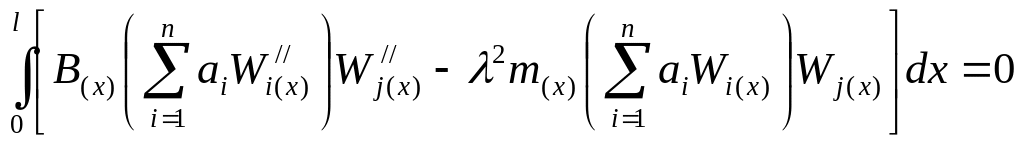
В матричном виде эта система запишется как

(54)

где ; - квадратные матрицы;

- искомый вектор неизвестных параметров.

;

Данное матричное уравнение приводится к следующему стандартному виду:

(55)

где

Таким образом, задача о собственных колебаниях балки сведена к задаче о собственных значениях и векторах характеристической матрицы , для решения которой имеются стандартные программы. Форма изгибных колебаний -го тона будет

Пример. Разработать алгоритм задачи о вынужденных колебаниях консольной балки под действием распределенной нагрузки , где - круговая частота вынужденных колебаний балки ;

- частота колебаний в секунду (Гц).

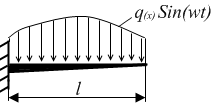
Решение ищем в виде . В этом случае правая часть уравнения (54) не будет равна нулю, так как в выражение (51) войдут еще и внешние нагрузки:

, (56)

где ; .

Уравнение (56) сводится к системе алгебраических линейных уравнений, так как задана

где .

В данном решении не учтены диссипативные силы, поэтому при (резонанс) D=0 и компоненты вектора принимают бесконечные значения.

В случае учета диссипативных сил (внешнее и внутреннее сопротивление) матрицы , и вектора и будут комплексными.

4. Метод Релея в сочетании с последовательными приближениями.

Позволяет определить низшую частоту собственных колебаний механических систем и является частным случаем метода Ритца. Метод Релея основан на принципе Гамильтона и одночленном представлении формы колебаний.

Так, в случае изгибных собственных колебаний балки, уравнение (25) приводится к виду:

, (57)

где - потенциальная энергия деформации в

момент наибольшего отклонения упругой

системы (балки);

- кинетическая энергия упругой системы

(балки) в момент прохождения ее через

положение равновесия.

Из (57) следует формула Релея:

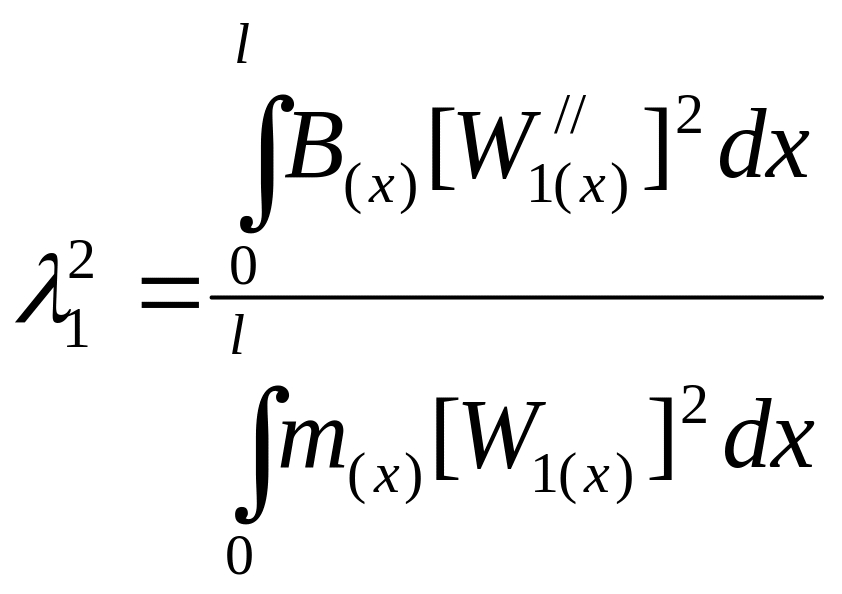, (58)

где , - погонные масса и жесткость балки.

Если дополнительно использовать последовательные приближения (итерации), можно уточнить форму колебаний и соответствующую ей частоту. Для этого используется дифференциальное уравнение колебаний механической системы. В случае изгибных колебаний балки используется уравнение:

, (59)

которое предварительно приводится к интегральному виду путем последовательного интегрирования уравнения и определения постоянных из граничных условий. После интегрирования (59) имеем:

(60)

В случае консольной балки: при :

при : ; .

Откуда следует, что ; ;

.

Запишем уравнение (60) в виде:

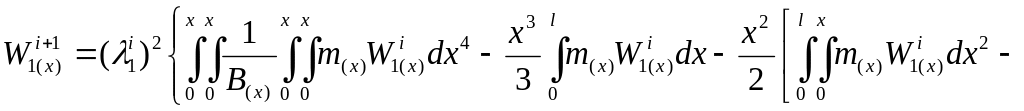
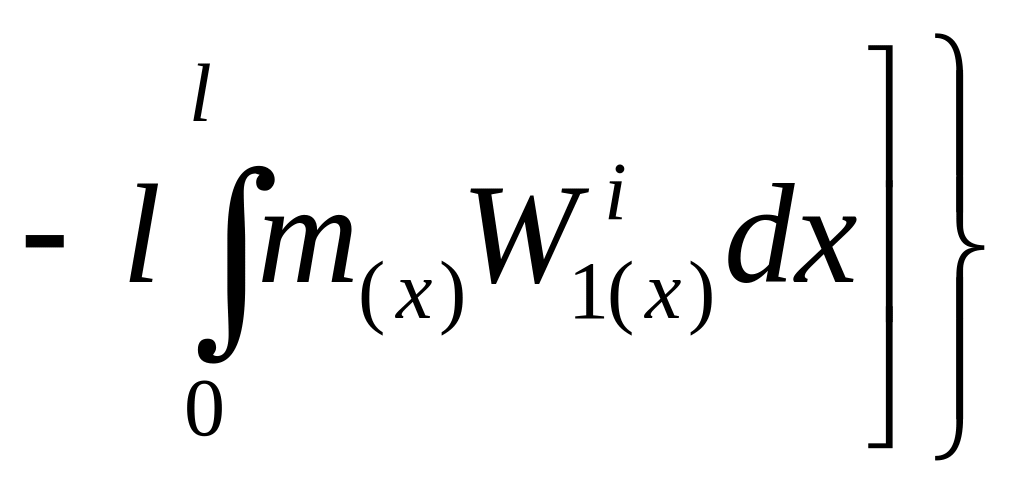. (61)

Тогда, задавшись , по формуле (58) определим , а затем по уравнению (61) определим и по формуле (59) - . Процесс итерации производится до тех пор, пока или норма не будет меньше наперед заданной погрешности.

Численные методы векторной механики.

Недостатком вариационных методов является необходимость задания для всей механической системы аппроксимирующих функций, которые не всегда легко определить. Методы векторной механики лишены этого недостатка.

Векторная механика приводит к дифференциальным, интегрально-дифференциальным и интегральным уравнениям относительно искомых величин. Эти уравнения можно решать с помощью аналитических методов, т.е. описать решение формулой, выраженной через элементарные функции.

Например, общим аналитическим решением уравнения является функция . Однако, если бы потребовалось решить несколько более сложное уравнение , то мы не смогли бы выразить его решение через элементарные функции. Так как уравнения данного типа встречаются часто, то было решено необходимым причислить их решения к числу так называемых специальных функций, дополняющих класс элементарных. Так появились в математике бесселевы функции. В результате класс дифференциальных уравнений, интегрируемых аналитически (в явном виде) расширился. Аналогично бесселевым функциям было введено много других специальных функций, связанных с решением тех или иных обыкновенных дифференциальных уравнений. Введение таких функций в обращение, требует их детального качественного изучения и составления подробных таблиц. Однако и эти функции не могут охватить многообразия решения всех встречающихся обыкновенных дифференциальных уравнений. Еще сложнее положение для дифференциальных уравнений с частными производными. Поэтому получение явных формул не может считаться наиболее выгодным процессом, ведущим к решению уравнений.

Однако этот процесс не утратил своего значения, так как остается очень мощным и необходимым инструментом при качественном исследовании решений. В связи с появлением ЭВМ мощное развитие получили численные методы решения уравнений векторной механики.

Сущность численного решения проиллюстрируем на примере уравнения

Запишем производную разностным соотношением , h-шаг разностной схемы. В результате получим приближенное разностное уравнение или в виде реккурентной формулы . Если задано начальное условие U(0)=U₀, то можно вычислить значения U(h), U(2h), U(3h) и т.д.

При U₀=1 имеем U(nh)=(1-ah)ⁿ. Выбрав h=1/n, получим U(1)= . Точное же решение U(1)=e^-a

Обе эти величины при достаточно большом n отличаются мало. Таким образом, метод конечных разностей позволяет получить приближенные решения в конечном числе точек.