- •Общие способы решения инженерных задач и соответствующие вычислительные машины.
- •Неалгоритмический способ. Физическое моделирование.
- •Вариационные и векторные методы решения задач механики.
- •1.Метод конечных разностей
- •2. Интегрирующие матрицы
- •Плоская задача теории упругости
- •Колебания стержневых систем
- •Объемная задача теории упругости (solid)
- •Приведение объемных и поверхностных сил, а также начальных деформаций к эквивалентным узловым внешним силам.
Плоская задача теории упругости
Треугольный плоский элемент с тремя узлами
Предположим, что дискретная модель разработана. Элементы соединены друг с другом в узлах.

Выделим из дискретной
модели КЭ с вершинами 1, 2, 3. Действие
отброшенных элементов заменим усилиями.
![]() .
.
Так как положение
КЭ в пространстве (на плоскости)
определяется вектором узловых перемещений
элемента
![]() ,
содержащим шесть компонентов узловых
перемещений, то это позволяет предположить
закон изменения по полю КЭ в виде:
,
содержащим шесть компонентов узловых
перемещений, то это позволяет предположить
закон изменения по полю КЭ в виде:
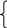
![]() (1)
(1)
![]() -
горизонтальное и вертикальное перемещения
текущей точки КЭ.
-
горизонтальное и вертикальное перемещения
текущей точки КЭ.
Или:
![]() ,
(2)
,
(2)
где
![]() - вектор перемещений.
- вектор перемещений.
![]() (3)
(3)
![]() .
.
Подстановка значений узловых координат в (2) дает:
![]() ,
(4)
,
(4)
где
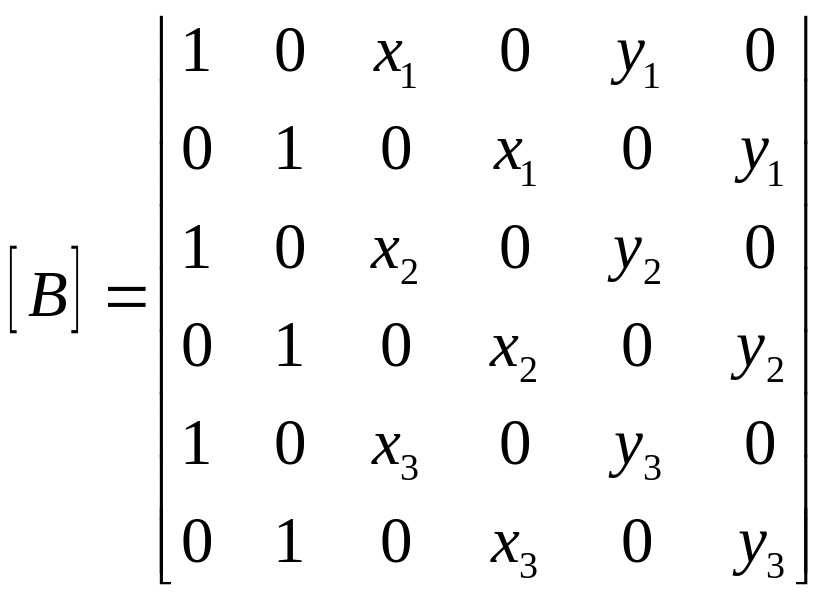 (5)
(5)
Отсюда
![]() (6)
(6)
Подставляя
![]() в (2), получаем связь между
в (2), получаем связь между
![]() и
и
![]() :
:
![]() ,
(7)
,
(7)
где
![]() .
.
Выражение (7) определяет распределение перемещений по полю элемента в зависимости от узловых перемещений и в развернутой форме имеет вид:
(8)![]()
![]()
где
![]() - удвоенная площадь треугольного КЭ.
- удвоенная площадь треугольного КЭ.
![]() ,
,
![]() (9)
(9)
Деформированное
состояние элемента характеризуется
вектором деформаций
![]() ,
компоненты которого определяются
зависимостями Коши:
,
компоненты которого определяются
зависимостями Коши:
![]()
![]()
![]() (10)
(10)
или в векторной форме с учетом (1) и (6):
![]() (11)
(11)
где
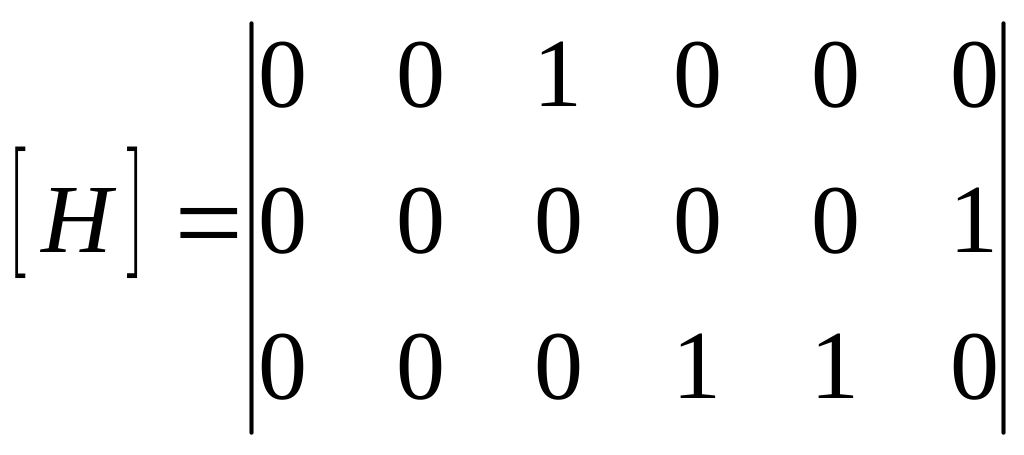 ,
(12)
,
(12)
получающаяся в результате дифференцирования выражения (1) по зависимостям Коши.
Развернутое выражение (11) получается из непосредственного дифференцирования выражений (8), т.е.:
![]()
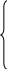
![]() (13)
(13)
![]()
или в матричной форме
![]() (14)
(14)
где
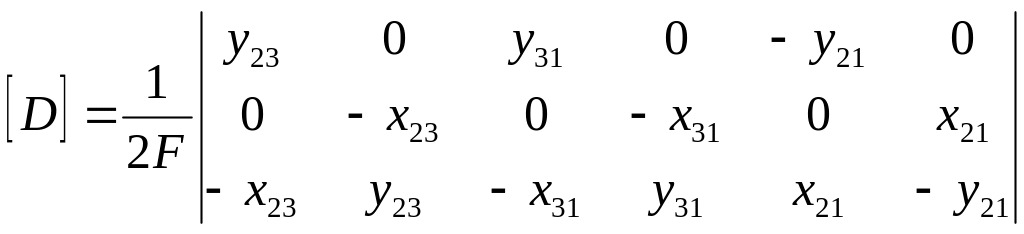
Из сравнения выражений (11) и (14) видно, что
![]() .
.
Напряженное
состояние элемента определяется вектором
напряжений
![]() ,
который на основании закона Гука ……….
материала связан с
,
который на основании закона Гука ……….
материала связан с
![]() зависимостью
зависимостью
![]() ,
(16)
,
(16)
где
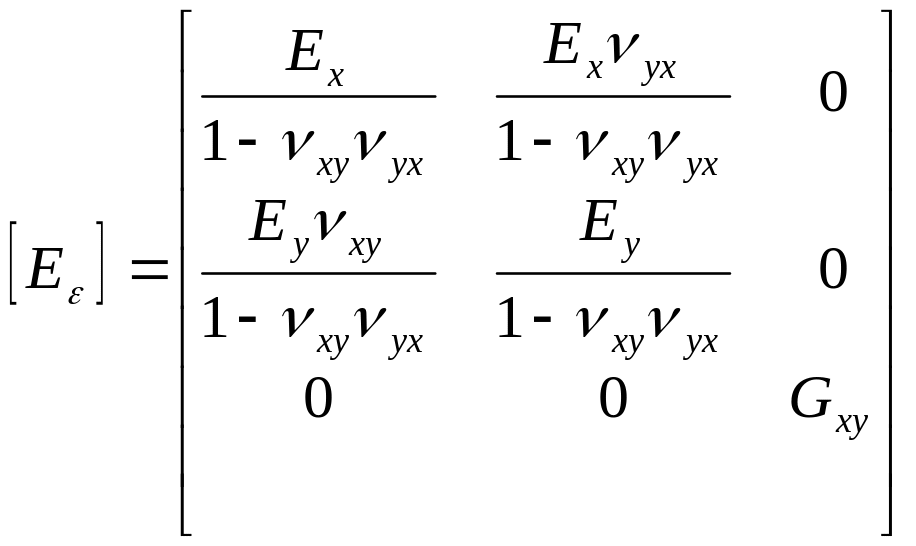 -
(17)
-
(17)
- матрица упругих характеристик материала.
Здесь
![]() ,
,![]() -
модули нормальной упругости соответственно
вдоль оси х и у;
-
модули нормальной упругости соответственно
вдоль оси х и у;
![]() -
коэффициент Пуассона. характеризующий
сокращение в направлении оси у при
растяжении вдоль оси х;
-
коэффициент Пуассона. характеризующий
сокращение в направлении оси у при
растяжении вдоль оси х;
![]() -
коэффициент Пуассона. характеризующий
сокращение в направлении оси х при
растяжении вдоль оси у;
-
коэффициент Пуассона. характеризующий
сокращение в направлении оси х при
растяжении вдоль оси у;
![]() -
модуль сдвига плоскости ху.
-
модуль сдвига плоскости ху.
Так как коэффициент
Пуассона и модули нормальной упругости
должны удовлетворять соотношению
![]() =
=
![]() ,
то матрица
,
то матрица
![]() симметрична.
симметрична.
Если исключить теперь с помощью (11) вектор из (16), то получим выражение, определяющее напряжения в КЭ по известным значениям его узловых перемещений
![]() ,
(18)
,
(18)
где
![]() - матрица напряжений, развернутое
выражение которой имеет вид
- матрица напряжений, развернутое
выражение которой имеет вид
![]()
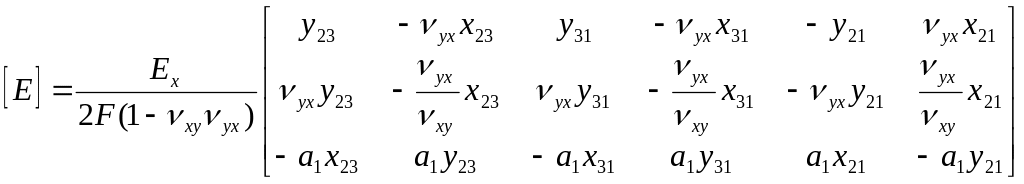 (19)
(19)
здесь
![]() .
.
Теперь, когда напряженное (18) и деформированное (11) состояние КЭ определяются через его узловые перемещения, можно определить матрицу жесткости КЭ.
Из теории упругости известно, что потенциальная энергия деформации КЭ определяется выражением
![]() ,
(20)
,
(20)
где h – толщина КЭ,
или в матричной форме
![]() (21)
(21)
Подставляя сюда (14) и (18) и учитывая правило транспортирования произведения матриц, получим:
![]() (22)
(22)
где
![]() - (23)
- (23)
- искомая матрица
жесткости КЭ, которая устанавливает
зависимость между узловыми усилиями и
узловыми перемещениями КЭ, т.е.
![]()
 (24)
(24)
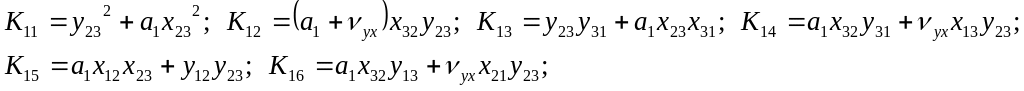
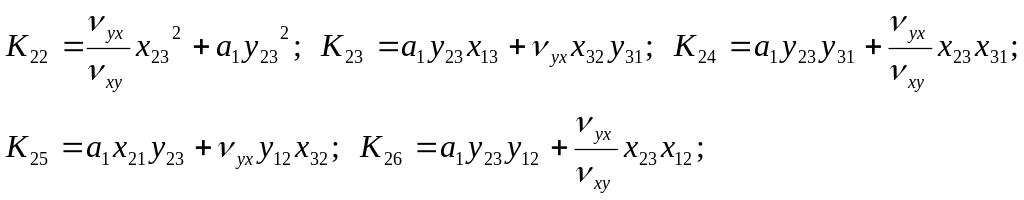
![]()
![]()
![]()
![]()
Выражение изгибающих моментов и перерезывающих сил по длине элемента будут иметь вид с исправлениями (26):
![]()
![]()
![]()
Условия, действующие на элемент в узлах, будут:
при x = 0:
![]()
![]()
при x = l:
![]()
![]()
В результате получим выражения, совпадающие с (13а). Отличие состоит только в знаках во второй и третьей строках.
Это связанно с принятым правилом знаков в МКЭ и правилом знаков при выводе дифференциального уравнения в сопротивлении материалов.
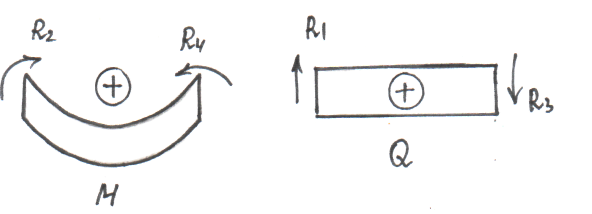
![]() и
и
![]() .
В результате с учетом знаков получаем
зависимость между узловыми усилиями и
распределенной нагрузкой.
.
В результате с учетом знаков получаем
зависимость между узловыми усилиями и
распределенной нагрузкой.

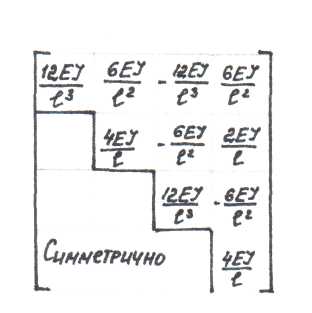 (30)
(30)
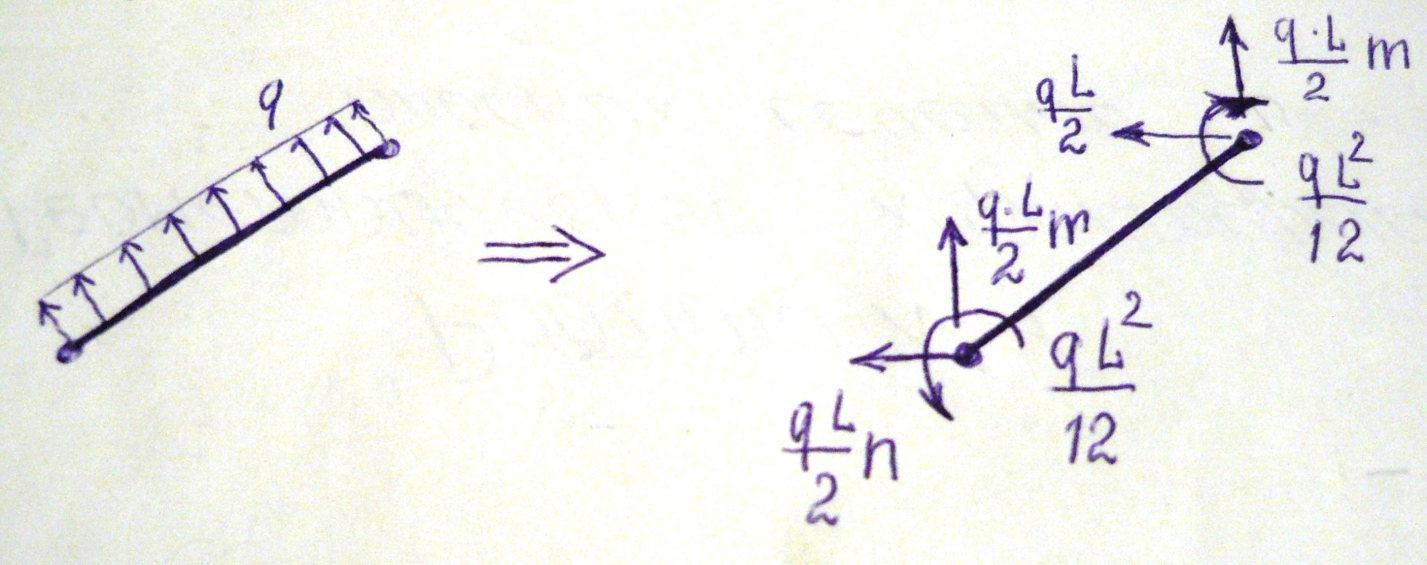
Последнее слагаемое определяет внешнюю узловую нагрузку, эквивалентную внешней распределенной нагрузке.

Такие реакции возникают в жесткозаделанной балке.

Балочный элемент, работающий на изгиб и растяжение-сжатие в одной плоскости.
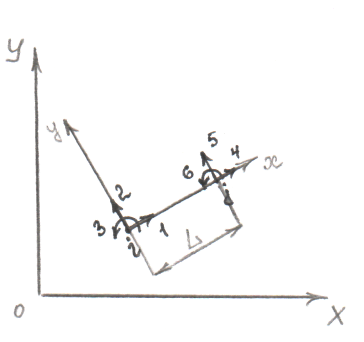
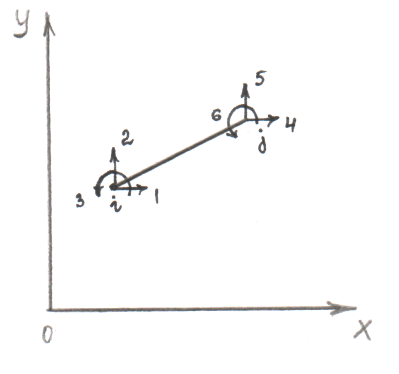 Для
получения МЖ призматического элемента
вводится система координат xoy
и общая система координат XOY
Для
получения МЖ призматического элемента
вводится система координат xoy
и общая система координат XOY
Элемент загружен
узловыми усилиями
![]() ,
ориентированные в местной системе
координат, и его положение определяется
вектором перемещений
,
ориентированные в местной системе
координат, и его положение определяется
вектором перемещений
![]() ,
ориентированных также в местной системе
координат.
,
ориентированных также в местной системе
координат.
Положение элемента полностью определяется шестью узловыми перемещениями, поэтому делается следующее предложение о законе измерения поперечного прогиба
![]() (31)
(31)
И продольных деформаций вдоль оси элемента
![]() , (32)
, (32)
где
![]() - коэффициенты, подлежащие определению.
- коэффициенты, подлежащие определению.
Использую (31) и (32) можно найти узловые перемещения
п ри
х =
0:
ри
х =
0:
![]() ;
;![]() ;
;![]() ;
;
при х
= L:
![]() ;
;
![]() ;
;
![]()
Отсюда можно
определить ![]() через узловые перемещения
через узловые перемещения
![]()
или в развернутом виде:
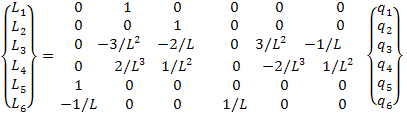 (35)
(35)
Потенциальная энергия деформации элемента в случае совместных изгибных и продольных деформаций имеет вид:
![]() (36)
(36)
где с учетом (31) и (34)
![]() (37)
(37)
![]() (38)
(38)
или
![]() (39)
(39)
![]() (40)
(40)
Подставив (39) и (40) в (36), получим
![]() (41)
(41)
Где ![]() (42)
(42)
- искомая матрица жесткости плоского блочного элемента в местной системе координат.
Производя интегрирование и перемножение матриц в (42), получим окончательное выражение матрицы жесткости призматического элемента в местной системе координат.
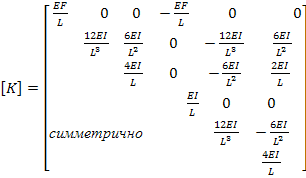 (43)
(43)
Матрицу жесткости (43) можно использовать в расчетах балочных конструкций, если направление общей системы координат совпадает с направлением местной системы (например, прямолинейная балка). Однако в реальных конструкциях (например, шпангоутная рама) элементы имеют различную ориентацию. Поэтому необходимо иметь матрицу жесткости в общей системе координат, тоесть узловые усилия и перемещения должны быть ориентированы как показано на рисунке. Для этого необходимо выразить узловые перемещения в местной системе через узловые перемещения в общей системе координат
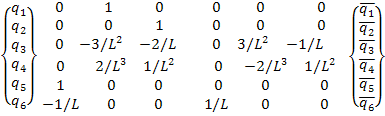 (44)
(44)
или ![]() (45)
(45)
где ![]() – матрица преобразования координат
(матрица направляющих косинусов). Она
является ортогональной, так как
– матрица преобразования координат
(матрица направляющих косинусов). Она
является ортогональной, так как ![]() ;
;
![]() ;
;
![]() – направляющие косинусы продольной
оси элемента относительно осей
– направляющие косинусы продольной
оси элемента относительно осей ![]() и
и
![]() .
.
![]() – длина элемента;
– длина элемента;
![]() координаты
узлов элемента в общей системе координат.
координаты
узлов элемента в общей системе координат.
Подставляя (45) в (41), получим потенциальную энергию элемента через его узловые перемещения в общей (глобальной) системе координат:
![]() (46)
(46)
Отсюда получаем матрицу жесткости в общей системе координат через матрицу жесткости в местной системе координат:
![]() (47)
(47)
![]()
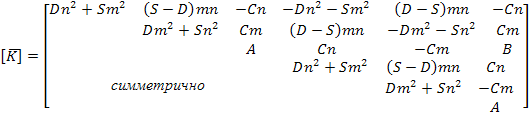
Чтобы оценить прочность КЭ, необходимо распологать знаниями его внутренних усилий, выраженных через узловые перемещения в общей системе координат. Это соотношение можно получить, если подставить (45) в (13):
![]() (48)
(48)
Где ![]() матрица
усилий, развернутое выражение которой
имеет вид:
матрица
усилий, развернутое выражение которой
имеет вид:
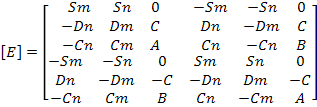
Определение эквивалентной узловой нагрузки
Пусть произвольно
ориентированный элемент загружен
поперечной нагрузкой. Требуется
определить эквивалентную узловую
нагрузку ![]() в общей системе координат.
в общей системе координат.
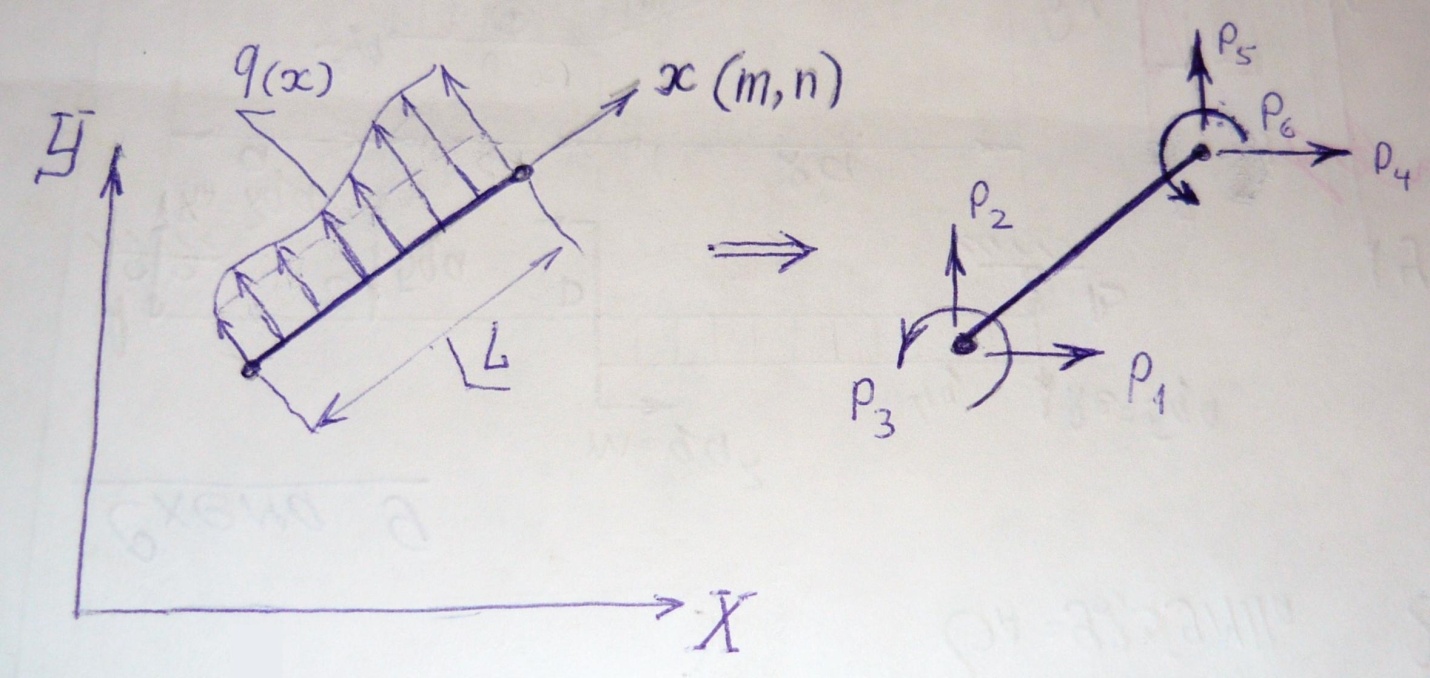 Для
определения
Для
определения ![]() воспользуемся принципом возможных
перемещений, на основании которого
можно записать:
воспользуемся принципом возможных
перемещений, на основании которого
можно записать:
![]() (49)
(49)
Т.е. работа эквивалентной узловой нагрузки на возможных перемещениях узлов равна работе распределенной нагрузки по длине элемента на возможных перемещениях его сечений.
Здесь ![]() – перемещение сечений перпендикулярных
оси КЭ.
– перемещение сечений перпендикулярных
оси КЭ.
Выражение (31) можно записать как:
![]() (50)
(50)
Или с учетом (34)
![]() т.е.
функция прогиба через узловые перемещения
в местной системе. Если сравнить с (28),
то видно, что в произведении
т.е.
функция прогиба через узловые перемещения
в местной системе. Если сравнить с (28),
то видно, что в произведении ![]() заложены функции Эрмита при изгибе.
заложены функции Эрмита при изгибе.
![]() т.е. функция прогиба через узловые
перемещения в глобальной (общей) системе
координат.
т.е. функция прогиба через узловые
перемещения в глобальной (общей) системе
координат.
Подставим вариацию
перемещений сечений ![]() в (49).
в (49).
![]()
Здесь учтено, что
матрицы ![]() и
от
и
от ![]() не
зависят
не
зависят
В результате, после
сокращения на ![]() ,
получим выражение узловых эквивалентных
усилий в глобальной системе координат
,
получим выражение узловых эквивалентных
усилий в глобальной системе координат
![]() (51)
(51)
В случае, если на
КЭ действует равномерно-распределенная
нагрузка ![]() ,
то
,
то
![]()
При принятом
правиле знаков для ![]()