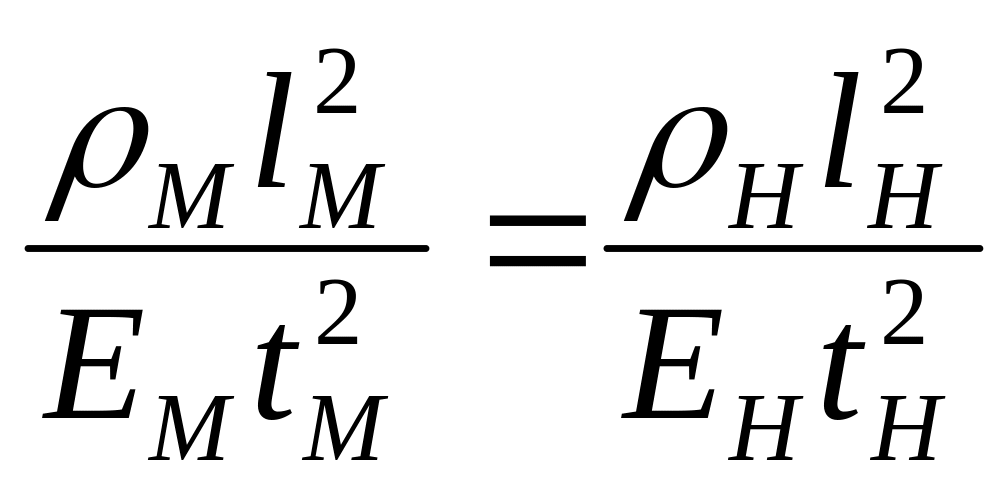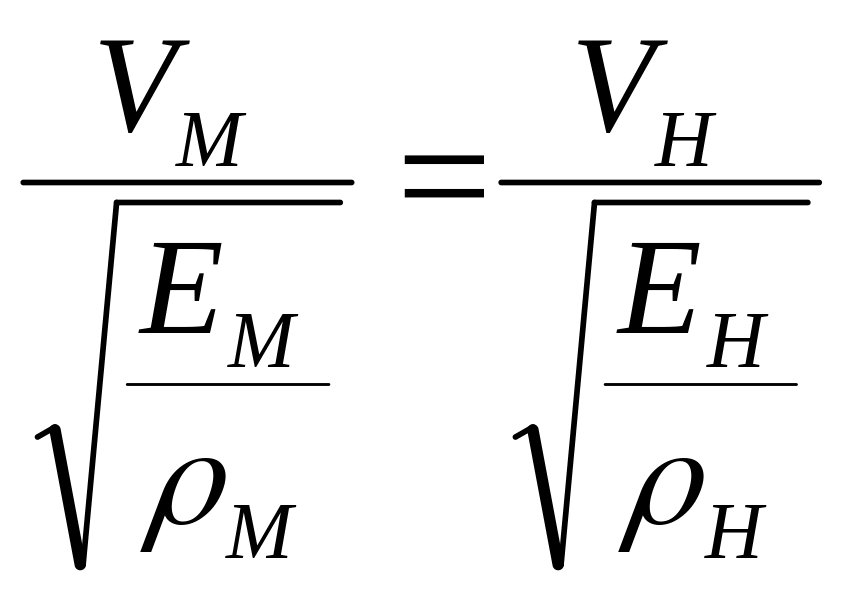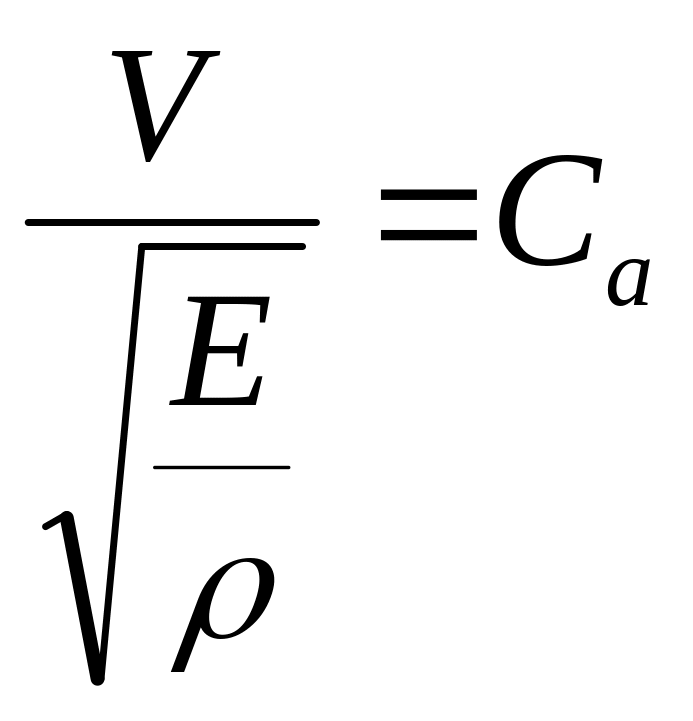Общие способы решения инженерных задач и соответствующие вычислительные машины.

Решение инженерных и научно-исследовательских задач может быть осуществлено с помощью алгоритмического, неалгоритмического и комбинированных способов.

Алгоритмический способ основан на математическом описании задачи, конкретном методе арифметизации процесса вычислений и алгоритме.

Алгоритм решения задачи - точное предписание о порядке выполнения элементарных операций (арифметических и логических) над исходными данными для получения результата. Для решения задач алгоритмическим способом применяются машины дискретного действия (ММДД: в порядке эволюции - механические, электромеханические, электронные арифмометры (калькуляторы), ЭЦВМ, ЭВМ…). Впереди, очевидно, искусственный специализированный интеллект-механотроника.

Неалгоритмический способ основан на теории физического или математического моделирования. В этом случае нет необходимости иметь алгоритм задачи, нужно лишь знать уравнения, описывающие задачу( при математическом моделировании) или физические параметры изучаемого явления( при физическом моделировании). Для решения задач неалгоритмическим способом были разработаны машины непрерывного действия (ММНД) – аналоговые вычислительные машины (АВМ), а также физические модели, играющие роль ММНД. К ММНД относятся: логарифмическая линейка, интеграторы, диффер-ые анализаторы, математические модели. В ММНД перерабатываемая информация представляется в непрерывной форме в виде меняющихся во времени (физических аналоговых величин), например, при установке на объект тензодатчика аналогом удлинения волокон детали будет электрический ток в тензодатчике, который можно оцифровать с помощью АЦП и поместить в виде файла в ПК и затем изучить.

Комбинированный способ основан на комплексном использовании неалгоритмического и алгоритмического решения задачи.

Алгоритмический

ММДД

Неалгоритмический

ММНД

Комбинированный

гибридный

Метод аналитической механики

Метод векторной механики

Смешанные методы

Метод физического моделирования

Метод математического моделирования

Неалгоритмический способ. Физическое моделирование.

Основан на понятии модели.

Модель – физическая система, которая определенным способом отображает вид и поведение объекта или процесса в натуре. Различают модели: геометрические, физические, математические.

Геометрические служат в основном для демонстрационных целей и дают представление в виде натуры.

Физическое моделирование – это, когда соответствующие величины имеют одинаковую физическую природу (модель судов, испытуемая в опытовом бассейне, модели конструкций, испытуемая в силовых устройствах.

Математическое моделирование- изучение натуры одной природы (механической, тепловой и т.д.) с помощью модели, имеющей другую физическую природу (электрическую, гидравлическую и т. п.), явления в которых описываются одинаковым математическим выражением. Модель в этом случае - математическая.

Физическое моделирование.

Физические модели строятся на основе теории подобия и учения о моделировании. В теории подобия изучаются свойства заведомо подобных тел или систем.

В учении о моделировании решается вопрос о том ,каким требованиям должна удовлетворять модель ,чтобы процессы ,происходящие в натуре и модели были подобными.

Основные правила физ. Моделирования:

1.Модель и натура должны быть геометрически подобны, то есть все соответствующие линейные размеры модели и натуры находятся в одном и том же отношении ,называемом масштабом геометрического подобия или линейным масштабом C_l.

Например: балка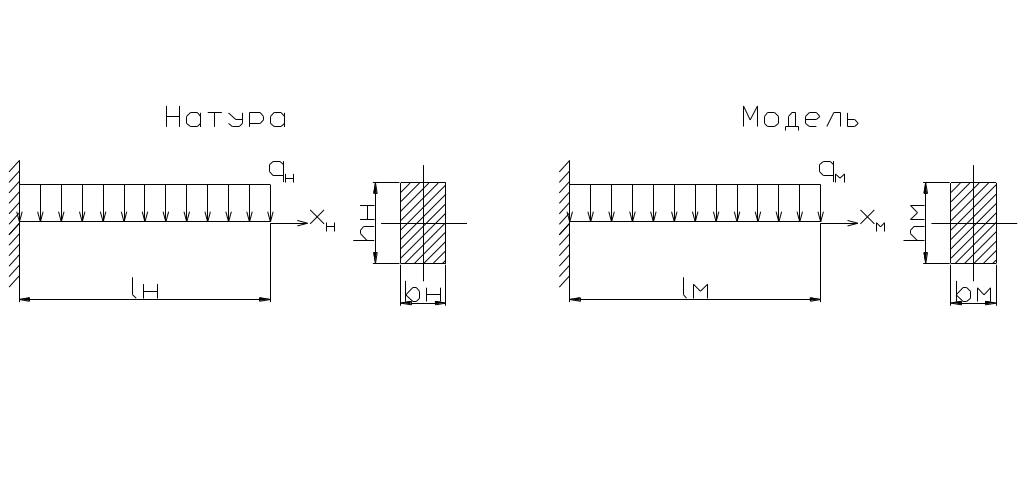

L_м/lн=h_м/h_н=b_м/b_н=С_l=const

Из геометрии подобия следует ,что

F_м/F_н=C_l² ; W_м/W_н=C_l³ ; I_м/I_н=C_l⁴

Где F, W. I –площадь, момент сопротивления и момент инерции в соответствующих сечениях модели и натуры.

2.Модель и натура должны быть кинематически подобны. Модель и натура называются кинематически подобными , если при соблюдении геометрического подобия отрезки времени , за которые соответственные точки модели и натуры опишут соответственные траектории ,находятся в одном и том же отношении ,называемом масштабом времени C_t= _м/ _н .

Из кинематического подобия следуют масштабы для скоростей ,ускорений и угловых скоростей

V_м/V_н=C_l/C_t ; a_м/a_н=C_l/C_t ² ; _м/ _н=1/C_t ;

3.Модель и натура должны быть динамически подобными .Модель и натура являются динамически подобными ,если при соблюдении кинематического подобия массы m в соответственных объёмах модели и натуры находятся в одном и том же отношении ,называемом масштабом масс C_m= _м/ _н

Из динамического подобия следуют масштабы плотностей масс и масштаб сил

_м/ _н=C_m/C_l ³ ; P_м/P_н= С_mC_l/C_t ²

4.Явление в модели и натуре должно принадлежать к одному и тому же классу ,то есть описываться одинаковыми дифференциальными уравнениями. Безразмерные начальные и краевые условия в модели должны тождественно совпадать с такими же условиями в натуре .Одноимённые безразмерные параметры ,входящие в дифференциальные уравнения модели и натуры ,начальные и краевые условия в модели должны быть соответственно равны.

Уравнения масштабов .Индикаторы подобия и критерии.

Выведем уравнения масштабов ,используя четвёртое правило моделирования на примере динамического изгиба балки.

Натура => 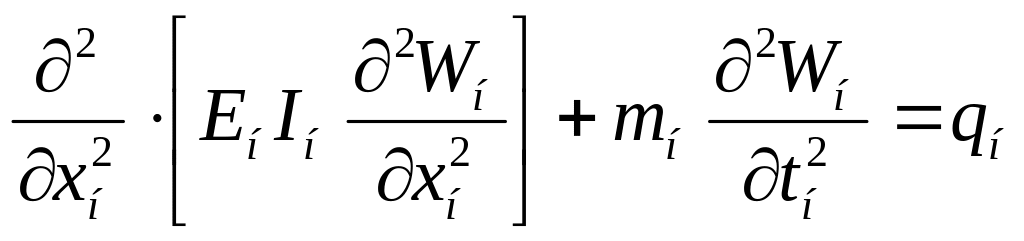(1)

Модель =>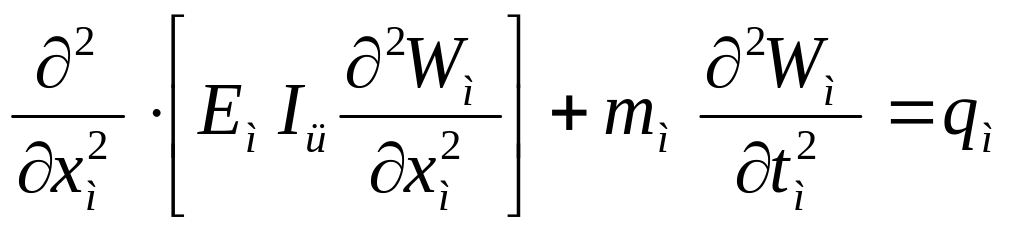 (2)

Е- модуль упругости;

m, q- погонные масса и нагрузка;

t- время;

W- прогиб балки;

I- момент инерции сечения.

Введем масштабы:

; ; ; ; ; ; . (3)

Выразим в (2) параметры модели через параметры натуры, используя соотношения (3):

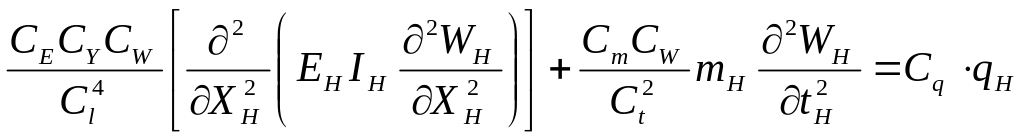(4)

Модель и натура будут подобны, если уравнение (1) будет отличаться от (4) лишь постоянным множителем, т. е. будут выполняться условия:

. (5)

Учитывая, что , , вместо уравнений (5) получим:

(6)

Условия (5) или (6), накладывающие ограничения на выбор масштабов (3), называют уравнениями масштабов. Они содержат 2 уравнения и 5 масштабов, т. е. 3 масштаба могут быть выражены произвольно и лишь 2 масштаба определяются из уравнений (6).

Разделим (6) на . Получим:

. (7)

Величины и − безразмерные комплексы, составленные из масштабов, называют индикаторами подобия данных модели и натуры.

Из (7) следует, что модель и натура подобны, если индикаторы подобия равны единице.

Учитывая, что

; ,

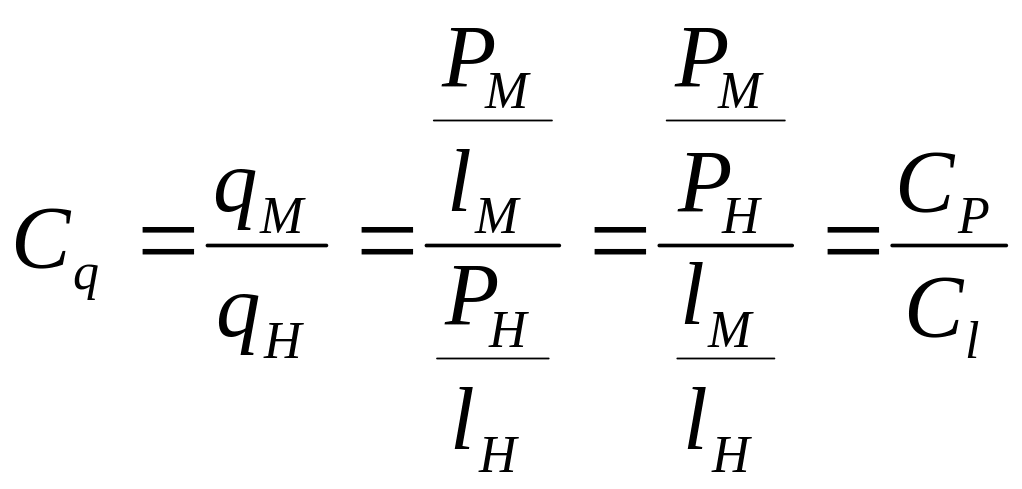где - масштаб сил.

Из (7) получим критерии подобия:

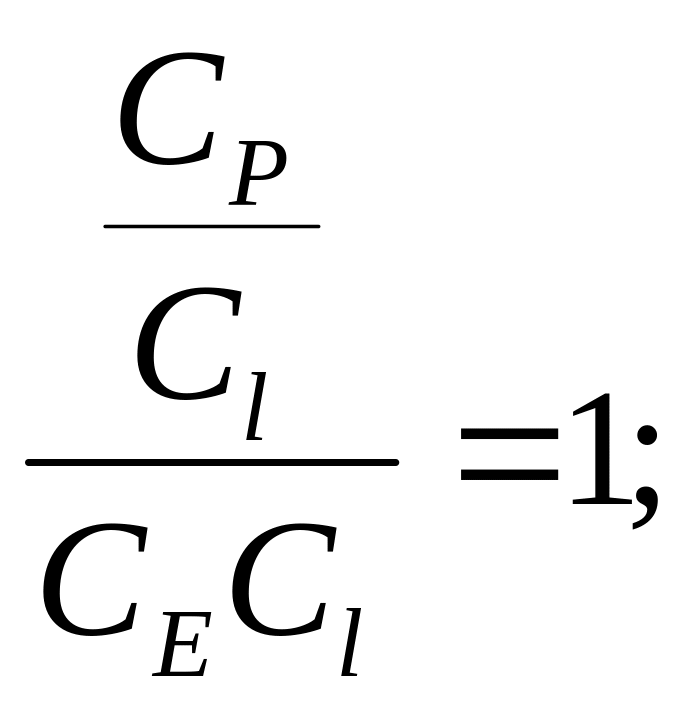
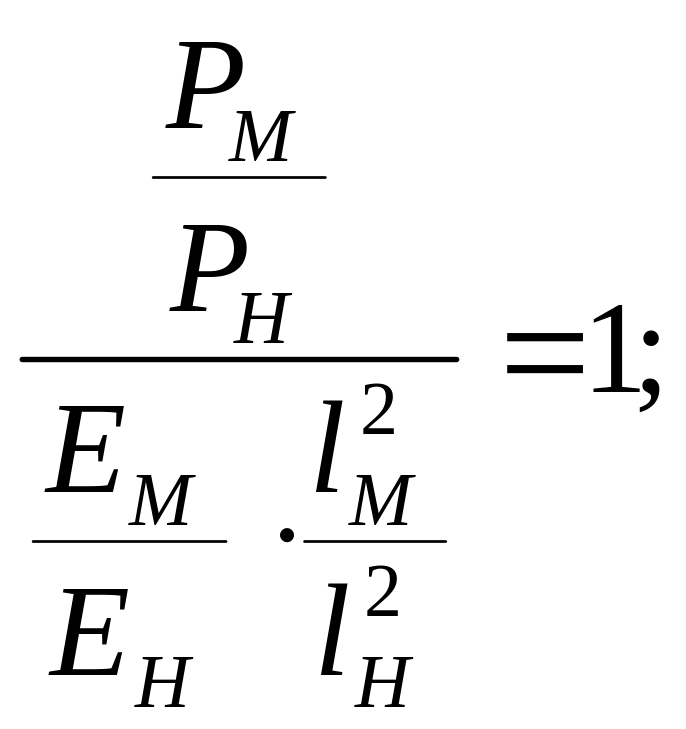
− критерий подобия. (8а)

с учетом, что и ,

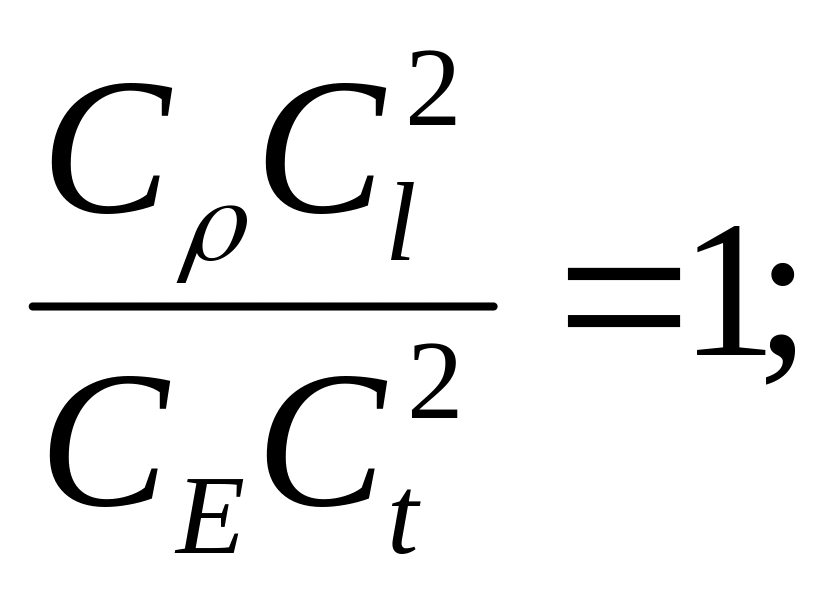
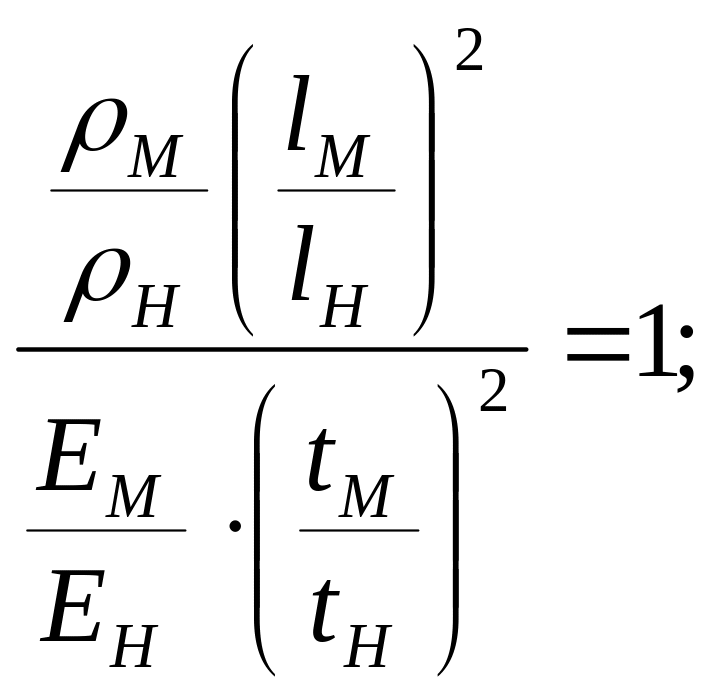
отсюда:

− критерий подобия. (8б)

В результате из (7) получили 2 критерия подобия, которые состоят из безразмерных комплексов (можно проверить по размерностям).

Безразмерный комплекс называется числом Гука.

Безразмерный комплекс называется числом Коши.

Таким образом, модель и натура подобны, если выполняются (8а) и (8б), т.е. числа Гука и Коши для модели и натуры одинаковы:

Но_м = Но_н , Са_м = Са_н ( 9 ).

Теория подобия позволяет по известным уравнениям процесса в натуре найти условия подобия и построить модель на основе искомых масштабов.

Метод анализа размерностей

Позволяет найти зависимость какой-либо физической переменной от всех существенных для данного процесса переменных и параметров. Предполагается, 1) что заранее известно, от каких параметров и переменных зависит интересующая нас физическая переменная; 2) что между всеми существенными для рассматриваемого процесса величинами имеет место функциональная связь.

Каждая физическая величина а характеризуется размерностью [а] (эталоном, с которым она сравнивается) и числовым значением А, т.е.

а = А [а] (10).

Любое физическое соотношение удовлетворяет условию: по обе стороны знака равенства находятся одноименные величины, т.е. величины, имеющие одинаковые размерности. Поэтому уравнение, описывающее какой-либо физический процесс, устанавливает функциональную связь не только между физическими величинами, входящими в это уравнение, но также и между их размерностями. Размерность [а], т.е. величина принятого эталона, может зависеть от размерностей (эталонов) других величин:

[а] = f ([а₁], [а₂],…, [а_k]) или [а] = [а₁]^α1 · [а₂] ^α2… [а_k] ^αk (11)

– формула размерности величины а через размерности определяющих её основных величин.

Если единицы измерений для величин а₁, а₂,…, а_k увеличить соответственно в µ₁, µ₂,…, µ_k раз, то согласно формулам (10) и (11) число, измеряющее а , вместо А будет равно А':

А' =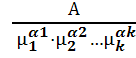

Эта формула удобна для перехода от одних единиц измерения к другим.

Если n физических величин а₁, а₂,…, а_k , а_k+1,…,а_n связаны меду собой уравнением

f (а₁, а₂,…, а_k , а_k+1,…,а_n )=0

и если размерности первых k величин [а₁], [а₂],…, [а_k] являются основными (т.е. их размерности независимы, и для них нельзя построить выражения типа (11) на основе k-1 размерностей), то размерности остальных n-k производных величин могут быть найдены как функции основных размерностей, т.е.

[а_k+1]= f _k+1([а₁], [а₂],…, [а_k])

[а_k+2]= f _k+2([а₁], [а₂],…, [а_k])

……………………………………..

[а_n]= f _n ([а₁], [а₂],…, [а_k]).

Важнейшим положением теории размерностей является I-теорема: всякое уравнение, связывающее между собой n+1 физических величин, среди которых k величин обладает независимыми размерностями, может быть преобразовано в уравнение, связывающее n-k+1 безразмерных комплексов, составленных из этих величин.

Доказательство.

Пусть известно, что физическая величина a связана с физическими величинами уравнением

(12)

в которой все величины имеют неодинаковые размерности. Причем первые k величин имеют независимые, а остальные величины ­ зависимые размерности.

Так как зависимые размерности могут быть выражены через независимые, то, принимая размерности величин , за основные, а размерности остальных величин за производные, получим следующие уравнения связи между размерностями:

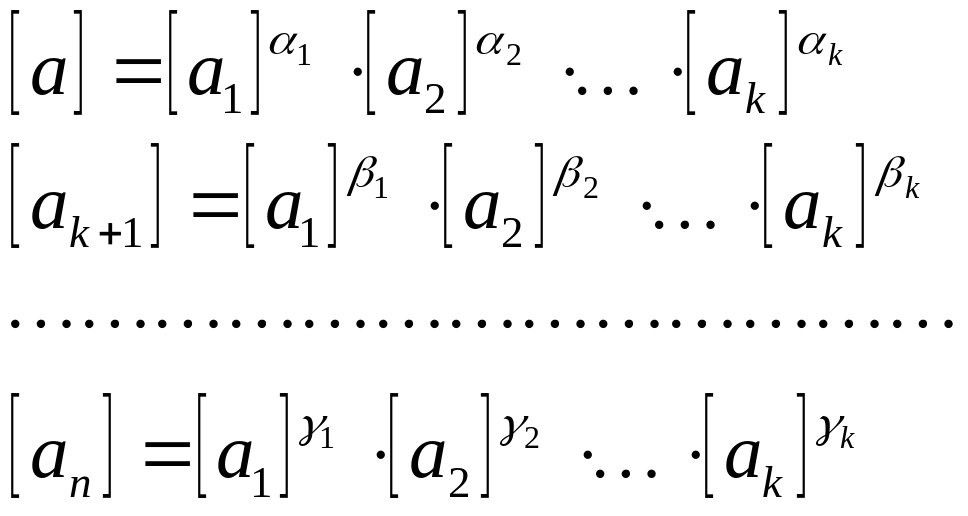
Из этих уравнений следуют безразмерные комплексы, для этого физическую величину a и зависимые физические величины разделим на независимые физические величины, взятые в соответствующих степенях их размерностей. При этом размерности сокращаются. В результате будем иметь:

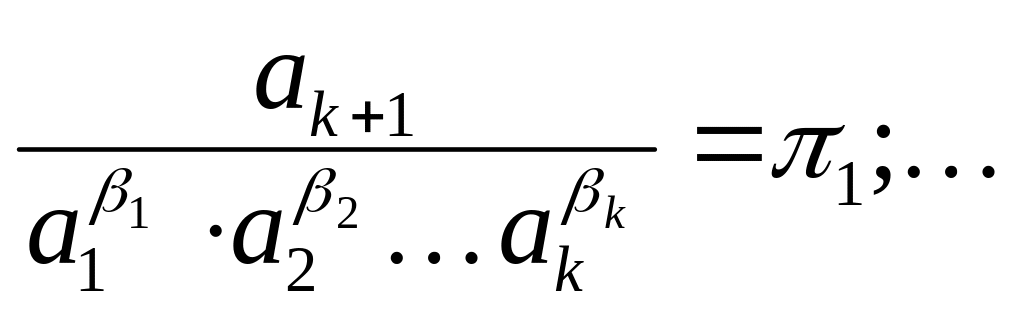
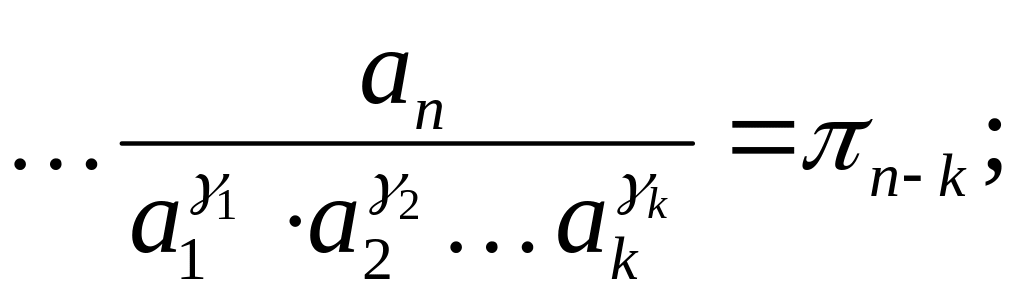(13)

Данные комплексы позволяют записать выражение (12) в виде

Примем за единицы измерения (эталоны), то есть увеличим единицы соответственно в раз. В результате получим:

(14)

Данное выражение представляет собой математическую формулировку π-теоремы. Безразмерные комплексы представляют собой одновременно критерии подобия модели и натуры. Число этих критериев равно n-k+1.

Следствия π-теоремы:

1. Из (14) следует формула для изучаемого процесса:

(15)

2. Модель и натура подобны, если и

3. При выборе масштабов физических величин k масштабов выбирают произвольно, а остальные n-k масштабов – из критериев

Физическое моделирование как метод решения задач

Используя теорию подобия или размерностей, можно определить масштабы, отображающие отношение параметров искомого физического процесса, с их помощью построить модель и результаты испытаний модели пересчитать на натуру, то есть получить искомое решение задачи.

Физическое моделирование обладает следующими достоинствами:

1. Более полно воспроизводит свойства натуры, чем математическое моделирование, т.к. в модели исследуются те же явления природы, что и в натуре. Эксперимент позволяет создать более точную теорию явления.

2. Позволяет изучать явления, которые не поддаются математическому описанию.

Недостатки:

1. Необходимость создания новой модели при исследовании каждого объекта.

2. Дороговизна моделей сложных объектов и необходимость высокой точности копии натуры

3. Трудность обеспечения точности измерения исследуемых величин.

4. Ограничение применения модели влиянием силы тяжести, действующей на все массы независимо от их расположения в системе.

Неалгоритмический способ.

Математическое моделирование.

Этот способ решения задач основан на свойстве полиморфизма двух явлений, имеющих различную физическую природу, т.е. на подобии по форме математических выражений, описывающих данные явления. Математическое моделирование является технической реализацией аналогий между Натурой и Моделью с целью получения численных значений для натуры по данным измерений в модели. Математическая модель позволяет производить по существу решение уравнений, описывающих процессы в натуре, т.е. служит математической машиной непрерывного действия или АВМ.

Пример: Определить реакции опор R_A и R_B в натуре, используя электрическую модель.

Натура Модель

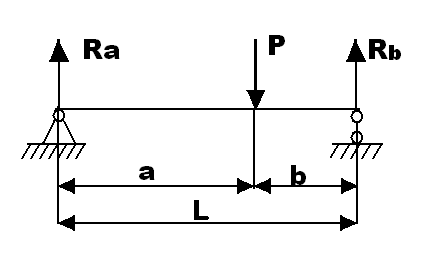
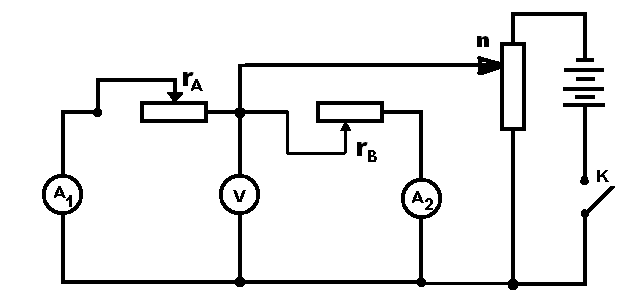
Решение:

Запишем уравнения для натуры и модели и определим электрические аналоги для механических величин.

Из уравнения равновесия балки натуры имеем

;

Из закона Ома для модели следует, что

;

Уравнения для натуры и модели изоморфны.

Примем ; ; ; где

- масштабные множители.

Тогда уравнение закона Ома для модели можно привести к виду

,

Отсюда следует, что

; , где

Электрическими аналогами для будут соответственно

Пример: Определить закон движения механической системы натуры, используя электрическую модель.

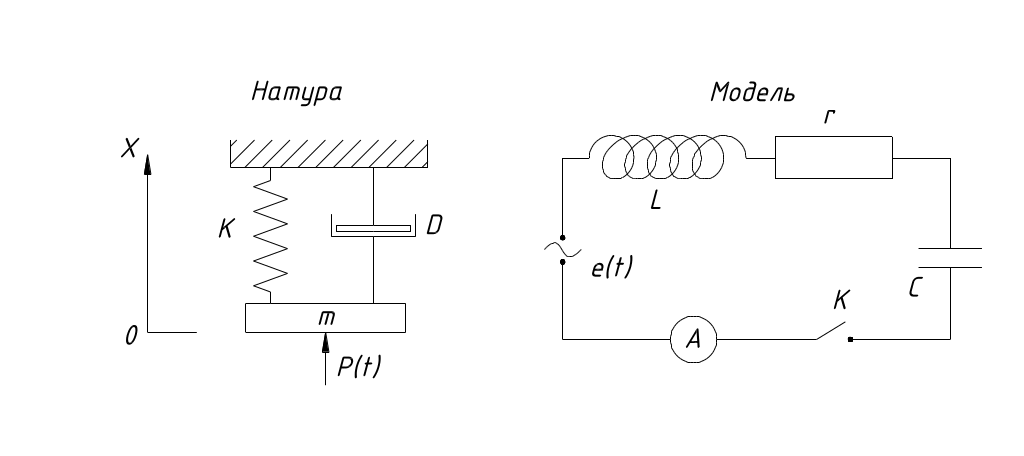
Для натуры принцип Даламбера: Сумма всех сил, приложенных к массе, должна быть равна нулю.

Для модели закон Кирхгофа: сумма падений напряжений плюс ЭДС внешнего источника в замкнутой цепи модели должна быть равна нулю.

Данные дифференциальные уравнения изоморфны. Здесь аналогами для механических величин натуры являются электрические величины модели:

Электрическая модель является АВМ, служащей для определения Х, .

Из приведённых примеров следует, что АВМ состоит из модели, устройства внешнего воздействия (источника) и измерительного устройства, которое может быть проградуировано в механическую величину, АВМ данной группы называют моделями-аналогами. При данном моделировании производится расчленение частей, образующих модель, по физическим элементам, которые математически изоморфны физическим элементам натуры. Здесь масштабы величин модели и натуры определяются согласно рассмотренным ранее уравнениям масштабов, индикаторам подобия и критериям подобия.

АВМ структурного типа конструктивно состоят из отдельных операционных блоков, каждый из которых воспроизводит какую-либо одну математическую операцию (сложение, умножение, дифференцирование, интегрирование, преобразование Фурье, преобразование Лапласа и т.д.), т.е. операционные блоки структурной АВМ изоморфны математическим операциям. В соответствии с видом решаемых уравнений из таких блоков создаётся схема АВМ, почленно отображающая математические операции решаемой задачи.

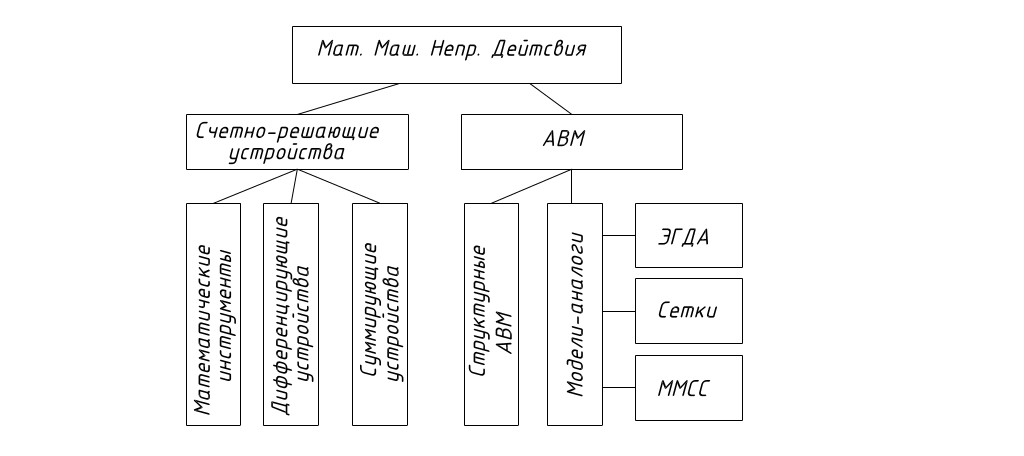
Счетно-реагирующие устройства: логарифмическая линейка, планиметры, калькуляторы, различного рода различные анализаторы, позволяющие выполнять отдельные операции в инженерных задачах.

Структурные АВМ. Используются в качестве математических моделей обыкновенных дифференциальных уравнений для интегрирования систем дифференциальных уравнений 1-ого порядка с начальными условиями (для решения задач Коши).

при

при

К системам данного типа приводятся задачи по динамическому нагружению элементов конструкций, предварительно дискретизированных методом сеток, конечных элементов или вариационными моделями.

Так как в АВМ данного типа одна физическая величина – время может выступать в роли независимой машинной переменной, то они не способны воспроизводить решения дифференциальных уравнений в частных производных.

При необходимости получения решения краевой задачи она предварительно сводится с помощью специальных методов к эквивалентной задаче Коши. Этот метод получения эквивалентной задачи называют редукцией краевой задачи к задаче Коши.

Например, в случае изгиба балки:

Краевые условия:

при при

Уравнение приводится у следующей системе с начальными условиями при :

или в развернутом виде

(прогиб)

(угол поворота)

(изгибающий момент)

(перерезывающая сила)

(распределенная нагрузка)

Здесь a и b – неизвестные величины, - неизвестные функции.

Эта система решается на АВМ методом проб: задается ряд значений a и b до тех пор, пока не выполняется условия на другом конце балки:

Решению задачи на АВМ предшествует процесс анализа исходных данных и выявления способа соединения операционных блоков АВМ. Этот процесс называют программированием АВМ.

АВМ – модели – аналоги для дифференциальных

уравнений в частных производных.

Данные ВМ более специализированы по сравнению со структурами АВМ. В модели – аналоге при моделировании производиться расчленение частей, образующих модель, не по отдельным математическим операциям, а по физическим элементам. При этом физические элементы модели изоморфны математически физическим элементам натуры. Все подлежащие исследованию элементы физической системы натуры представлены соответствующими физическими элементами – аналогами модели.

Основная цель использования моделей – аналогов заключается в определении поведения натуры, исследование которой связано с большими трудностями. Широкое использование для этих целей электрических моделей объясняется:

1. простотой изготовления;

2. доступностью электрических элементов для измерения;

3. независимостью электрических полей от сил тяжести и большинства внешних полей при условии надежного экранирования;

4. простотой электрических измерительных приборов в обращении;

5. универсальностью, все основные типы задач механики сплошных сред можно решать на электрических моделях.

Имеется одна закономерность, которая часто встречается в природе, выраженная уравнением Лапласа: . Она встречается более чем в десяти различных явлениях (теплота, распределение электрического потенциала, механика сплошных сред, колебания упругих тел, свет, звук, электромагнитное излучение и т.д.). Эти явления природы изоморфны.

АВМ – электрогидродинамической аналогии (ЭГДА) позволяет интегрировать уравнение Лапласа. Она используется для определения полей температур, магнитного поля, электростатического поля в диэлектрике, гидродинамического поля в идеальной жидкости. ЭГДА состоит из модели области определения искомой функции, выполненной из электропроводной бумаги, делителя напряжений, измерительного блока и блока питания. ЭГДА проста по конструкции, удобна в эксплуатации и не требует конечно-разностного представления уравнения Лапласа.

Схема ЭГДА для определения распределения скоростей жидкости вокруг сечения крыла

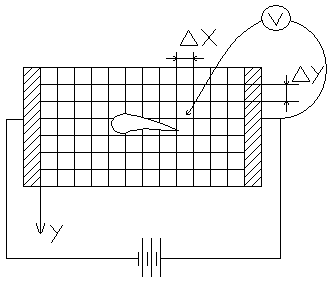
Решение задачи об определении потенциала скоростей φ(x,y) осуществляется путем снятия щупом-иглой значений напряжений в точках Модели. Зная потенциал скоростей, легко найти скорости жидкости вокруг крыла. На ЭГДА наиболее просто воспроизводятся краевые условия 1-го рода ( ) и 2-го рода ()

АВМ – сетки. Разработаны для интегрирования дифференциальных уравнений Лапласа ( ), Пуассона ( ), Фурье ( ) при краевых условиях 1-го, 2-го, 3-го рода (линейной комбинации условий 1-го и 2-го рода). Предварительно данные уравнения приводятся к системам алгебраических уравнений с помощью конечно-разностных соотношений.

Электрическая модель для уравнения Лапласа состоит из сетки активных сопротивлений, и задача об определении функции заменяется задачей измерения напряжений в узлах сетки

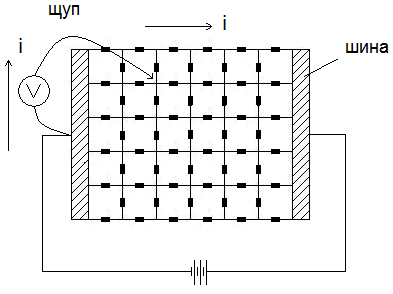
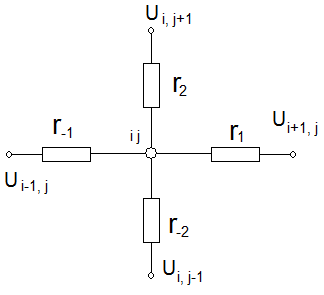
Для точки ij натуры уравнение Лапласа в конечно – разностном виде представляется выражением

(*)

Для точки ij модели на основе Киргофа сумма токов, входящих и выходящих из узла ij, равна нулю: где

; ; ; ;

Пусть , . Тогда закон Киргофа для точки ij

(**)

(i,j=1,2,…n)

Система уравнений (*) и (**) математически изоморфны. Задавшись масштабом , можно по напряжениям, снятым щупом из узлов сетки модели, определить значения функции φ в узлах натуры.

Промышленность выпускает различные АВМ – сетки, в частности ЭМ-6-БУ – электрическая модель бигармонических уравнений вида , позволяющее исследовать напряженное состояние в балках и плитах при изгибе сосредоточенными силами и решать плоские задачи теории упругости.

Математические модели стержневых систем (ММСС)

Это АВМ для раскрытия статической неопределимости многопролетных балок, плоских и пространственных рам. Они собираются из электрических аналогов отдельных стержней, к концам которых приложены изгибающие и скручивающие моменты.

В настоящее время разработаны компьютерные модели стержневых систем, которые реализованы в различных пакетах на основе конечно – элементарного анализа ( COSMOS, ANSYS, и другие).

Достоинства АВМ:

1. высокая надежность;

2. быстрота решения задачи;

3. не требует разработки алгоритма задачи;

Недостатки АВМ:

1. являются специализированными;

2. ограниченная точность решения (2÷10%)

Алгоритмический способ

Этот способ завоевывает наибольшую популярность в силу развития ЭВМ, ее периферии и стандартизации различных численных методов, вплоть до появления вычислительной и компьютерной механики

Этот способ не требует обязательного отыскания аналитического решения задачи и предполагает лишь наличие математического ее описания и алгоритма – системы формальных правил, четко и однозначно определяющих процесс вычисления, который пользователем реализуется на одном из языков программирования.

Этапы решения задач на ЭВМ:

1. Математическое описание задачи

2. Выбор численного метода (объем памяти, времени, точности и т.д.)

3. Разработка алгоритма решения задачи

4. Программирование на одном из алгоритмических языков или объектно-ориентированное программирование

5. Отладка программы

6. Решение задачи на ЭВМ и ее тестирование