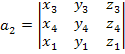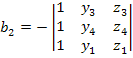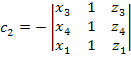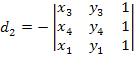Объемная задача теории упругости (solid)

Предполагается, что объемное тело заменено совокупностью объемных элементов, соединенных между собой лишь в узловых точках.

М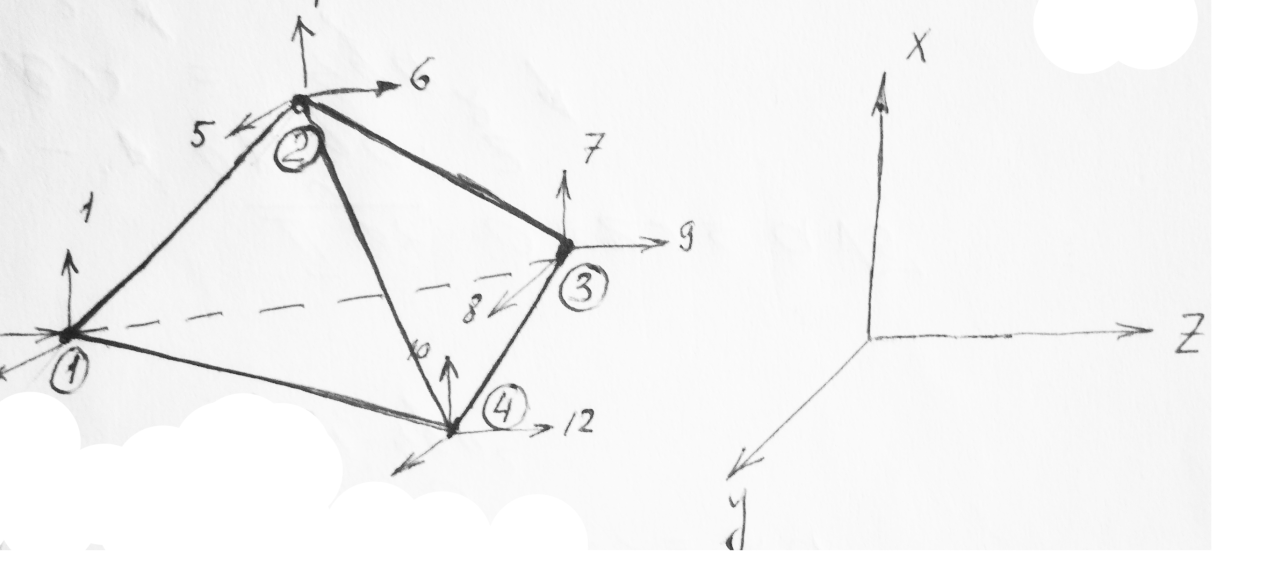 атрица жесткости для тетраэдра

- узловые перемещения

- узловые усилия

Так как 12 узловых перемещений, то вводим 12 коэффициентов α, что позволяет сделать предположение о линейной зависимости компонентов перемещений для произвольной точки от координат:

(37)

Или в матричной форме

(38)

где

1 х y z 0 0 0 0 0 0 0 0

0 0 0 0 1 x y z 0 0 0 0 (39)

0 0 0 0 0 0 0 0 1 x y z

Подстановка значений узловых координат дает

(40)

В результате

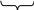
(41)

В развернутой форме выражение для имеет вид

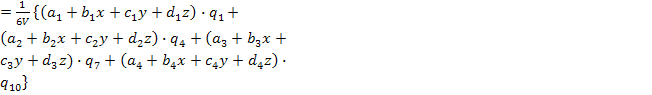(42)

Где

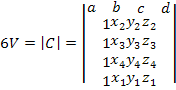-(43) определитель матрицы координат узлов, равных шести объемам тетраидального элемента

Значения других постоянных определяются с помощью круговой перестановки узловых индексов 1, 2, 3, 4.

Аналогичное выражение получаем для и . Отличие будет состоять только в том, что в выражения будут входить узловые перемещения вдоль осей и соответственно (аналогично выражениям (8)).

Д

(44)

ифференцируя компоненты перемещений (42) по зависимости Коши:

Найдем выражения для компонентов деформаций

(45)

Где

x

	0	0		0	0		0	0		0	0
0		0	0		0	0		0	0		0
0	0		0	0		0	0		0	0
		0			0			0			0
0			0			0			0
	0			0			0			0

(46)

Напряженное состояние

(47)

Где

Для изотропного материала

1	λ	λ	0	0	0
	1	λ	0	0	0
		1	0	0	0
			µ	0	0
				µ	0
					µ

Где, E-модуль упругости, -коэффициент Пуассона

Проводя аналогичные рассуждения, как и по формулам (20)-(23), получаем матрицу жесткости для 4-х узлового объемного элемента

(48)

К

Из матрицы [A] по зависимостям Коши

оторая устанавливает зависимость между узловыми усилиями и узловыми перемещениями КЭ, т.е. . Или в развернутом виде, удобном для исключения ошибок при реализации на ЭВМ

(50)

Можно заранее подсчитать вручную

Осесимметричная объемная задача теории упругости.

Тело вращения разбивается на совокупность кольцевых КЭ с треугольным или четырехугольным поперечным сечением.

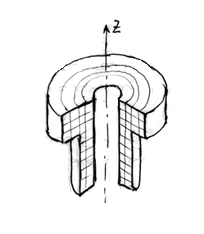
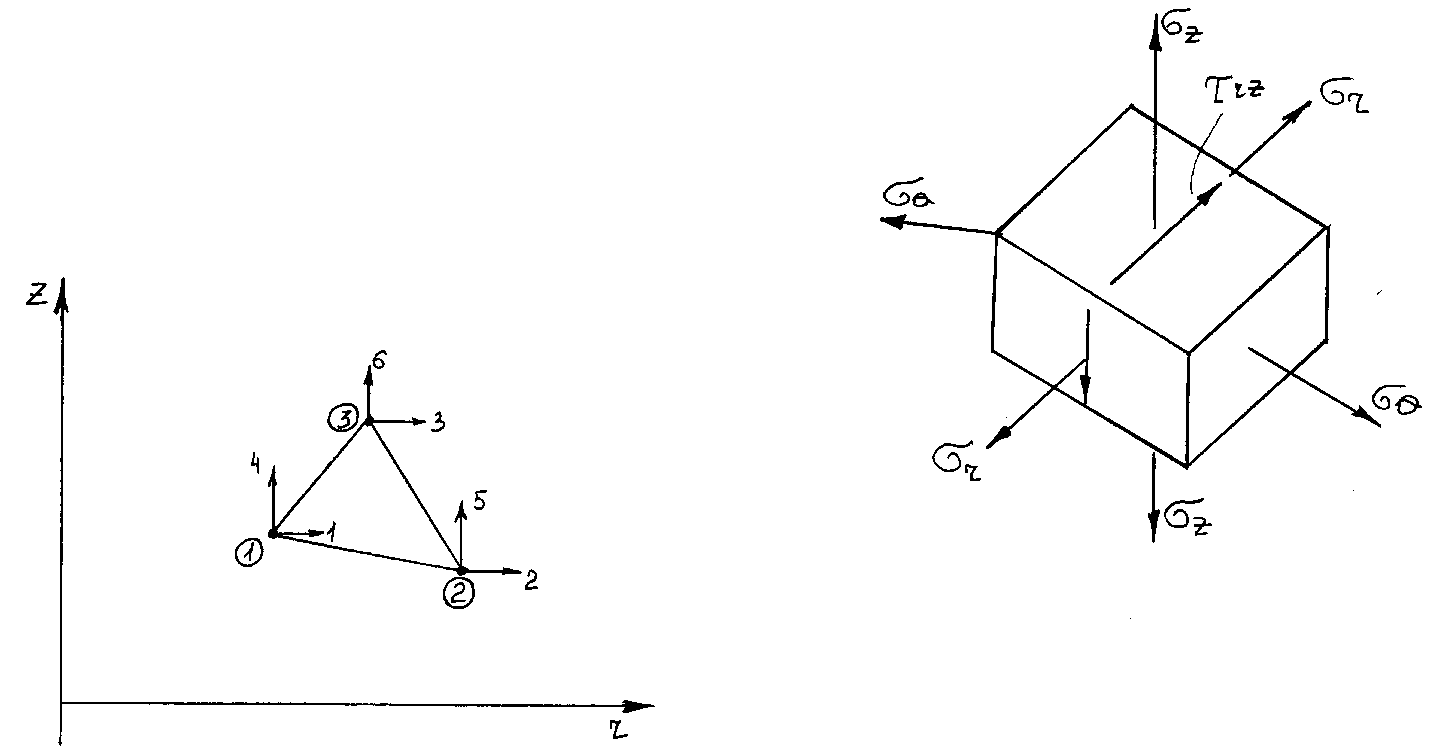
При осесимметричной форме тела и нагрузке напряженное и деформированное состояния будут функциями лишь координат r и z. Поэтому данная задача во многом аналогична плоской задаче теории упругости.

Матрица жесткости для кольцевого элемента с треугольным поперечным сечением.

КЭ представляет собой кольцо с треугольным поперечным сечением.

Так как шесть узловых перемещений, то это позволяет предложить закон изменения перемещений по плоскости поперечного сечения КЭ в виде

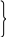
- радиальное перемещение

- осевое перемещение (51)

Или в матричной форме

, (52)

Где , (53)

Подстановка узловых координат в (51) дает

(54)

З десь - узловые перемещения

Радиальное осевое

перемещение перемещение

1
1
1
			1
			1
			1

(55)

Исключая с помощью (54) вектор из (52), получаем

, (56)

где

Зависимости Коши для осесимметричной задачи имеет вид

- радиальная деформация

- тангенциальная деформация

- осевая деформация (58)

- угловая деформация

- вектор деформаций

Отсюда, с учетом (56) и (57)

, (59)

где (60)

	1	0	0	0	0
	1		0	0	0
0	0	0	0	0	1
0	0	1	0	1	0

- в результате дифференцирования (61)

Закон Гука для изотропного материала запишем в виде

(62)

где

1			0
	1		0
		1	0
0	0	0

; ; (63)

или (64)

В результате имеем напряженное и деформированное состояния, выраженные через узловые перемещения.

Потенциальная энергия деформация КЭ

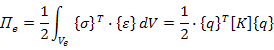
где (65)

или (66)

где (67)

F- площадь сечения кольцевого КЭ.

			0	0
			0	0
			0
			0	0	0
					0

Или в развернутом виде

где
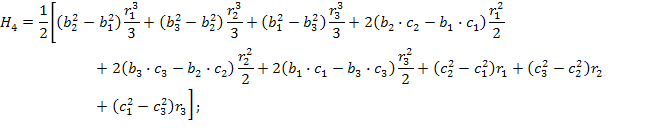
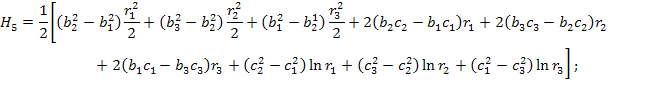
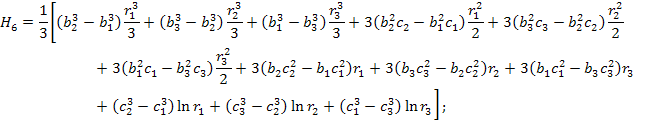