2. Интегрирующие матрицы

В случае уравнений, имеющих интегро-дифференциальный или интегральный взгляд, кроме конечно-разностных соотношений для производных, необходимо знать конечные соотношения для интегральных частей данных уравнений.

Всякую непрерывную функцию типа U(x) в области определения можно представить в виде вектора , где U_i – значение функции при х=х_i. Произведение можно представить в виде матричного выражения:

, где

- диагональная матрица,

-вектор

Используя правило трапеций, выражение можно записать в виде ,

где ; ;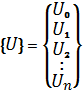

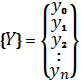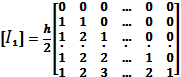
h – шаг сетки

- интегрирующая матрица преобразования вектора значений подынтегральной функции в вектор интеграла с переменным верхним пределом.

Можно показать, что интегралам ,

соответствуют матричные выражения

;

3.Численное решение задач механики, сводящиеся к задаче Коши.

Задачи по нестационарному нагружению тел (импульсивному, ударному) содержат краевые и начальные условия и описываются дифференциальными уравнениями в частных производных. Если в данных уравнениях производные по линейным координатам записать через конечно-разностные соотношения для каждой точки сеточной области тела, то вместо уравнений в частных производных получим системы обыкновенных дифференциальных уравнений по времени относительно искомых неизвестных в узлах сеточной области с заданными начальными условиями по времени.

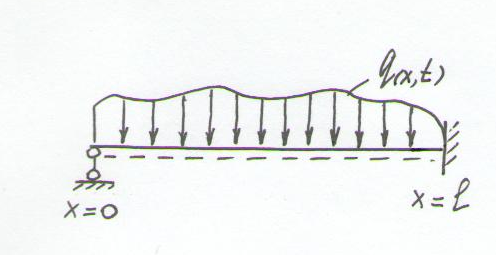
Пример. Определить деформированное состояние балки при ударном её нагружении.

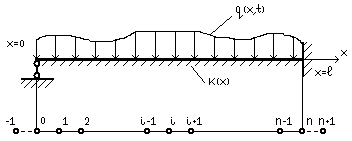
Дифференциальное уравнение для записывается:

(77)

При граничных условиях: х=0 w=M=0

х=l w=w`=0

и начальных условиях при :

Использовав конечно-разностное соотношение (71) для узлов сеточной области, вместо (77) получим:

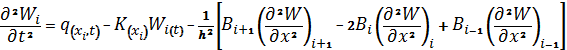(78)

где = ; i=1,2,3…; h - шаг сетки

В матричной форме (78) для

(79)

Здесь - диаганальная матрица масс

– диаг. матрица жесткости упр. основания

- вектор перемещений узлов

Начальные условия при : – начальные перемещения и скорости.

Обозначим ; ;

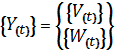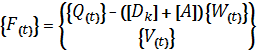
Тогда уравнение (79) запишется как

(80)

При начальных условиях

В результате пришли к задаче Коши в виде системы обыкновенных диф. уравнений (80) первого порядка, для которых можно применить численные методы интегрирования, реализованные на ЭВМ в виде стандартных подпрограмм.

Проиллюстрируем методы интегрирования уравнения (80).

а) Метод Эйлера

Запишем (80) в конечных разностях вперед:

(81)

i=0, 1, 2,…(узла во времени)

Тогда, зная, что при t=t₀ , можно последовательно найти для t_i (i=1, 2, 3,…). То есть, получаем трехмерную матрицу, когда квадратные матрицы идут по слоям друг за другом по времени с шагом ∆t.

Для оценки погрешности метода на одном шаге сетки (по времени) разложим точное решение в ряд Тейлора в окрестности временного узла t_i.

(82)

Сравнение (81) с разложением (82) показывает, что они согласуются до членов первого порядка по ∆t, а погрешность (81) равна {0}(∆t²). Если расчетные формулы численного метода согласуются с разложением в ряд Тейлора до членов порядка (∆t^p), то число p называют порядком метода или порядком аппроксимации. Т.о. метод Эйлера - метод первого порядка.

б) Метод Эйлера-Коши.

Проинтегрируем (80) на отрезке времени (t_i, t_i+1). В результате получим

(83)

Здесь и далее для упрощения записи фигурные скобки опущены.

Интеграл (83) запишем в конечном виде с помощью формулы трапеции по времени

(84)

В этом методе сначала определяется Y_i+1 по формуле (81), а затем уточняется по выражению (84).

в) Метод Рунге-Кутта.

Это метод повышенной точности интегрирования уравнений (80). Если метод Эйлера имеет порядок аппроксимации ∆t, метод Эйлера-Коши – (∆t)², то данный метод – (∆t)⁵. В этом случае

где (85)

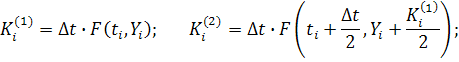
Для метода Рунге-Кутта имеются стандартные подпрограммы, в которых осуществляется автоматический выбор шага ∆t, обеспечивающий заданную относительную или абсолютную погрешность интегрирования (80).

Метод сеток (конечных разностей) обладает, по сравнению с вариационными методами, следующими достоинствами:

1. универсальностью;

2. слабой зависимостью вычислительной схемыот краевых условий (краевые условия влияют лишь на первые и последние несколько строк матриц)

3. Слабой заполненностью матриц, коэффициенты которых определяются более простыми выражениями по сравнению с матрицами вариационных методов.

Недостатки метода сеток:

1. Матрицы уравнений несимметричны и иногда плохо обусловлены ( малая вариация одного из коэффициентов матрицы приводит к большим изменениям величины её определителя), что приводит к погрешностям в решении. Признаком хорошей обусловленности матрицы является расположение коэффициентов с максимальными по модулю значениями на главный и примыкающий к ней диагоналях.

2. Сложность формирования системы уравнений при граничных условиях, заданных в силах.

Смешанные методы.

1. Вариационно-разностный метод.

Пусть задан функционал задачи (функционал Лагранжа или потенциальная энергия системы). В данном методе вариационная задача относительно искомых непрерывных функций заменяется вариационной задачей относительно дискретных значений этих функций в заданных узлах сеточной области искомой механической системы. Для этого все производные в функционале выражаются через конечно-разностные соотношения, а интегралы через суммы. Вектор значений искомой функции определяется из дискретизированного уравнения

т.е из системы

(i=1,2,…n), (86)

где - компоненты вектора , т.е. решения задачи.

Пример. Определить деформированное состояние изогнутой оси балки.

Функционал данной задачи имеет вид

(87)

Используя правило трапеций, представим интегралы в виде суммы:

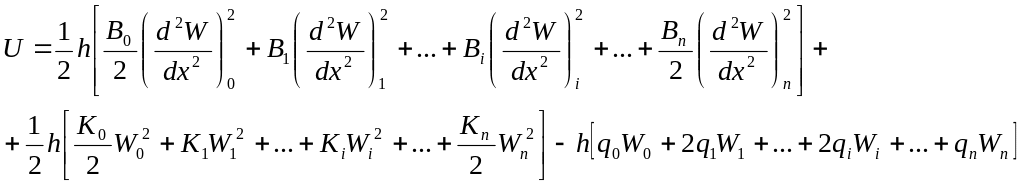(88)

где ;

;

;

После дифференцирования (88), согласно (86), получим

(i=1,2…,n-1)

или в матричной форме ,

где - квадратная матрица, содержащая жесткости балки и упругого основания в узловых точках;

- вектор внешней нагрузки в узловых точках;

- вектор перемещения узлов

Вариационно – разностный метод в отличие от конечно – разностного (сеточного - приводит к симметричным матрицам; при том же шаге дает более точное решение задачи; позволяет одинаково просто решать задачи как в перемещениях, так и в силах, т.к. граничные условия естественным образом входят в функционал.

2. Вариационно – шаговый метод. Основан на сведении задачи для нестационарного деформирования тела (функционального или дифференциального уравнений) к задаче интегрирования системы обыкновенных дифференциальных уравнений с начальными условиями ( к задаче Коши), которая затем интегрируется численно с помощью метода Рунге-Кутта. Это преобразование осуществляется обычно либо методом Ритца, либо методом Бубнова-Галеркина. Решение ищется в форме ряда, состоящего из произведений функций времени и координат.

Пример : определить деформированные состояния балки при ударном нагружении вариационно-шаговым методом.

Дифференционное уравнение для балки имеет вид:

(89)

Решение ищем в форме

(90)

где - аппроксимирующие функции, удовлетворяющие всем граничным условиям в случае использования метода Бубнова-Галеркина

- неизвестные функции.

Применим процедуру Бубнова-Галёркина к(89):

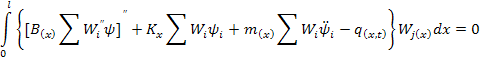
j=1,2,…n (91)

Обозначим

,

Тогда система (91) в матричной форме для t>t₀:

(92)

При начальных условиях

,

Здесь

;

Эта система сводится к стандартному виду (80)

d = ,при начальных условиях = ,где ;

; ;

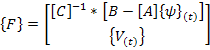Стандартная программа метода Рунге-Кутта позволяет определить вектор {Y},а следовательно, и исходную функцию прогибов (90).

Метод конечных элементов(МКЭ).

Сущность МКЭ.

В МКЭ начинают не с дифференциальных или интегральных уравнений, описывающих поведение среды, а с разработки дискретной модели и изучения свойств элементов конечных размеров. При установлении этих свойств могут использоваться уравнения, описывающие поведение сплошной среды, но размеры элементов среды остаются всё время конечными .Конструкция с бесконечным числом степеней свободы представляется дискретной моделью, имеющей конечное число степеней свободы.

Как вариационно-разностный метод, МКЭ основан на предварительной дискретизации деформируемого тела и на условии минимизации функционала (потенц. Энергии системы, функционала Гамильтона и т.д.)относительно неизвестных узловых перемещений или внутренних узловых усилий.

Сущность МКЭ на примере изгиба балки.

Рассмотрим на примере статич. Изгиба балки сущность МКЭ и основные этапы его приложения.

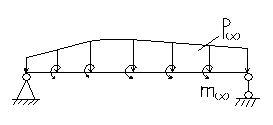
а)Пострение дискретной модели балки.

РАзобъём балку по длине с помощью узловых точек (узлов) i=1,2,3,…,n. Действие распределённой нагрузки P_(x) и m_(x) приближённо заменим нагрузкой, сосредоточенной в узлах. Перемещения балки будут характеризоваться перемещениями её узлов (каждый i-ый узел имеет два перемещения: W_i-прогиб и φ_i-угол поворота).

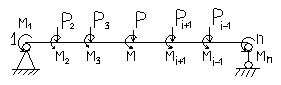
б)Построение зависимостей ,характеризующих упругие свойства элемента.

Для этого выделим е-ый КЭ, между узлами i и i+1. Действия соседних элементов заменим узловыми усилиями, которые сгруппируем в виде вектора-столбца.

{R}_e={R_i^(e) m_i^(e) R_i+1^(e) m_i+1^(e)}^T

Положение элемента в пространстве будет характеризоваться перемещениями его узлов, которые запишем также в виде вектора столбца.

{q}_e={W_i^(e) φ_i^(e) W_i+1^(e) φ_i+1^(e)}^T

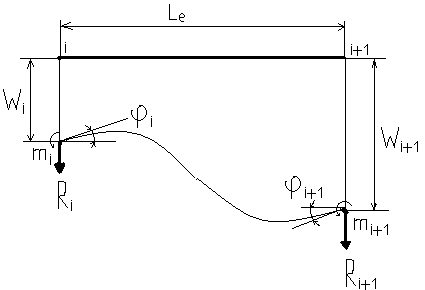
Рассмотрим функцию W_e(x) , аппроксимирующие поперечные перемещения e-го КЭ в пределах его длины l_e . Поскольку КЭ загружен лишь в узловых сечениях, то функция прогиба должна удовлетворять однородному дифф. Уравнению

EI_eW_e(x)^lV=0 (1)

Уравнению (1) тождественно удовлетворяет полином 3-ей степени

W_e(x)=α₁+ α₂X+ α₃X²+ α₄X³ (2)

или, в матричной форме,

(3)

где - матрица строка

- вектор столбец неизвестных пока коэффициентов.

Из анализа граничных условий -го конечного элемента следует, что:

при ; ;

при

Отсюда получим в матричной форме:

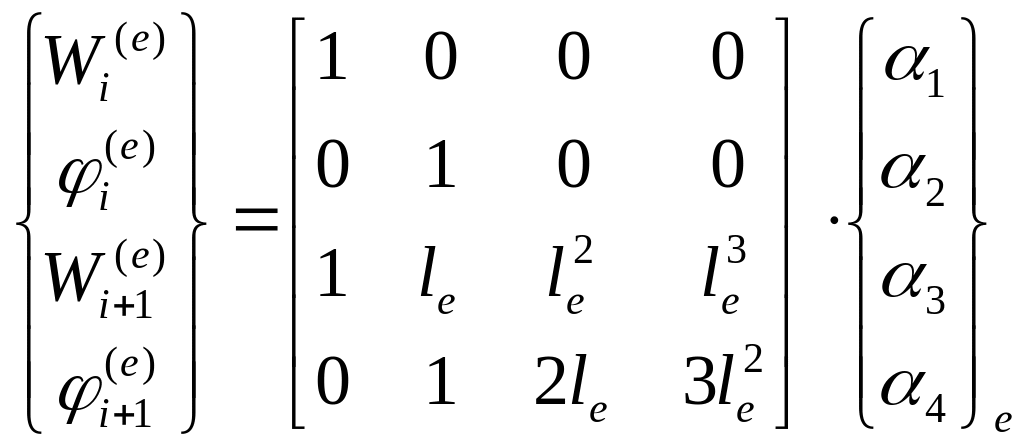(4)

или (5)

Так как число узловых перемещений КЭ (два прогиба и два угла поворота) равно числу неизвестных коэффициентов полинома (2), то можно определить значения коэффициентов полинома через узловые перемещения, то есть , подставляя которое в (3), найдем выражение прогиба по длине КЭ через значения его узловых перемещений:

(6)

Теперь зная функцию прогиба по длине КЭ, выраженную через значения его узловых перемещений, можно определить его потенциальную энергию -го конечного элемента также через значения его узловых перемещений:

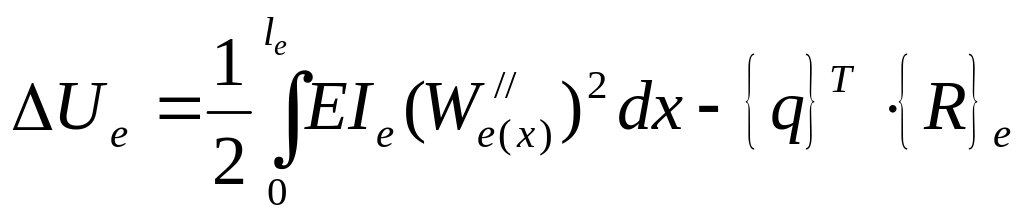(7)

где вторую производную найдем после дифференцирования выражения (6):

(8)

или (9)

Подставляя (9) в (7) и учитывая правило транспонирования произведения матриц, получим:

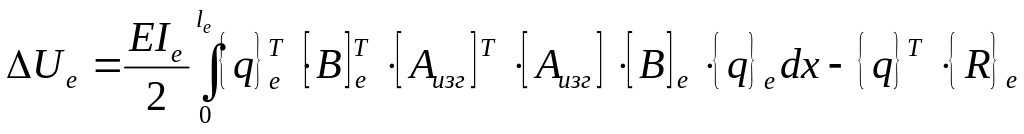(10)

или (11)

где 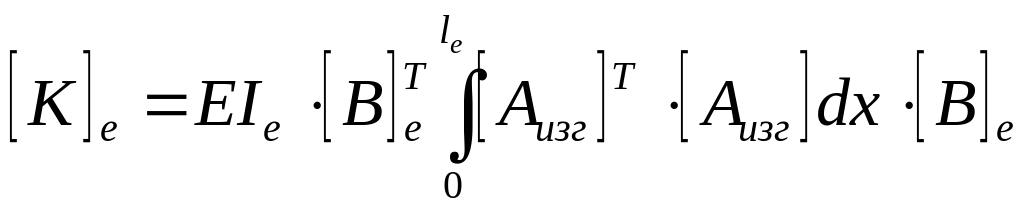- матрица жесткости -го элемента. Она полностью определяет жесткостные свойства рассматриваемого КЭ. Потенциальная энергия деформации -го элемента определяется первым слагаемым в выражении (11), т.е.

(12)

Таким образом, чтобы получить матрицу жесткости произвольного элемента, достаточно располагать выражением для потенциальной энергии деформации КЭ в форме (12).

Минимизируя потенциальную энергию КЭ (11), получим выражение, которое описывает равновесие -го КЭ:

(13)

Установление зависимости (13) между узловыми перемещениями и узловыми усилиями является основным этапом при исследовании МКЭ. В развернутом виде (13) для рассматриваемого балочного КЭ имеет вид:

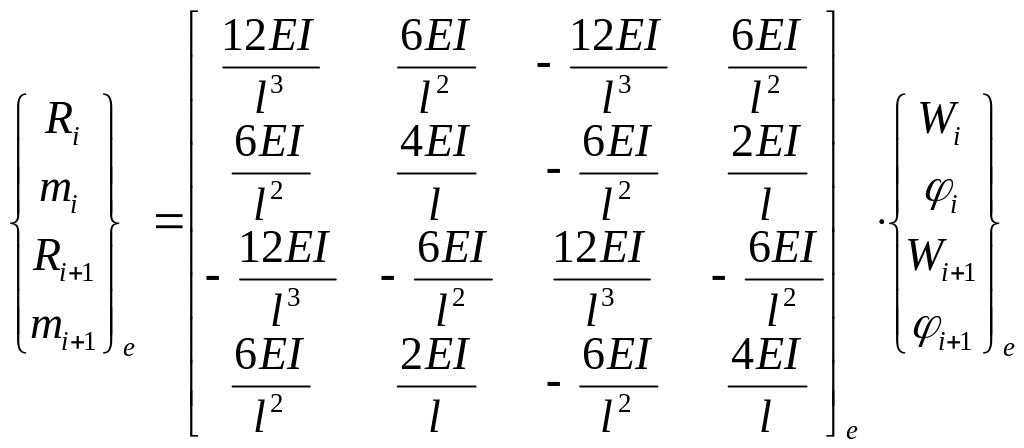(13а)

в) Построение системы разрешающих алгебраических уравнений.

Потенциальная энергия дискретной модели балки определяется выражением:

(14)

или с учетом (12)

(15)

где -

- вектор узловых перемещений балки

- вектор узловых усилий, эквивалентный внешней нагрузке, действующей на балку. Суммирование в (15) можно заменить операцией перемножения матриц, если ввести следующие матрицы: - вектор – столбец, состоящий из последовательно записанных перемещений каждого элемента;

-квазидиагональная матрица, состоящая из матриц жесткостей элементов, расположенных на главных диагональных блоках. Тогда (15) можно переписать как

U=1/2 (16)

Связь между векторами и устанавливается из их совместного рассмотрения (17)

– матрица связи. Для балки, состоящей из четырех КЭ

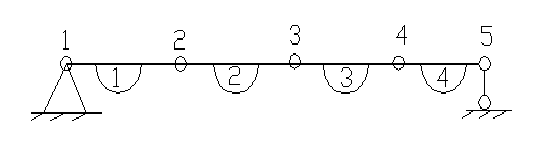
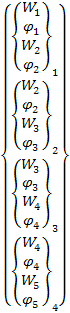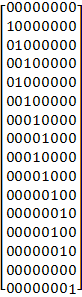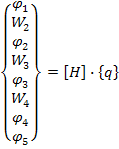= = ∙ (18)

Подставляя (17) в (16), получим окончательное выражение потенциальной энергии балки, выраженное в явной форме через перемещение ее узлов:

U=1/2 , (19)

где = (20)

- общая (глобальная) матрица жесткости балки. Она является симметричной (на основании теоремы о взаимности работ) и квадратной. Её порядок N равен общему числу узловых перемещений балки, т.е. в данном примере с учетом граничных закреплений, N=2∙n-2, n – число узлов.

Этот же порядок имеют вектора q и Q.

Минимизируя потенциальную энергию балки (19) по узловым перемещениям

; (i=1,2,…,n) (21)

получим систему линейных алгебраических уравнений

(22)

из решения, которой найдутся узловые перемещения балки (конструкции).

Физически уравнение (22) описывает условие равновесия узлов балки: сумма всех внешних усилий, приложенных в i-ом узле, должна равняться сумме всех усилий от конечных элементов, сходящихся в этом узле. Исходя из этого условия, можно сформировать систему уравнений. Например, рассмотрим равновесие 3-го узла балки

2

2

3

2

Уравнения равновесия 3-го узла балки будут иметь вид

→ + = P₃ → + = M₃ (23)

С огласно (13а) можно записать

(24)

В результате уравнения равновесия 3-го узла примут вид:

Последовательно рассматривая равновесие остальных узлов, можно составить необходимые уравнения. Однако подобная «ручная» процедура составления системы разрешающих уравнений хотя и проста по физической сути, но очень трудоемка при расчете даже простых конструкций. Она автоматически обеспечивается при перемножении матриц в выражение (20) с помощью ЭВМ. В то же время, получение глобальной матрицы жесткости К по выражению (20) для сложных конструкций связано с неудобствами и требует большого объема оперативной памяти ЭВМ, т.к. размеры матрицы связи Н могут достигать больших величин. Поэтому применяются более простые приемы автоматического формирования глобальной матрицы жесткости конструкции без ввода матрицы связи [H].

Математическая трактовка МКЭ

МКЭ можно трактовать как способ кусочной (поэлементной) аппроксимации непрерывной функции, определяющей решение задачи, множеством значений этой функции в некотором числе конечных точек (узловых точек или узлов) области ее определения в совокупности с кусочными (поэлементными) аппроксимациями этой функции на некотором числе подобластей. Эти подобласти называются конечными элементами. Аппроксимация функции внутри КЭ единственным образом определяется значениями этой функции(а возможно и значениями ее производных вплоть до некоторого порядка) в узлах, соединяемых этим КЭ.

Особенность использования МКЭ в задачах строительной механики состоит в том, что он применим к задачам, в которых можно минимизировать квадратичные функционалы. Другой важной особенностью МКЭ является то, что первоначально, при поэлементной аппроксимации, функции на КЭ-ах можно рассматривать независимо друг от друга. Это значит, что каждый элемент можно считать совершенно изолированным от всей совокупности и аппроксимировать функцию на этом же элементе с помощью ее значений в узлах независимо от того, какое место займет рассматриваемый элемент в связанной модели и от поведения функции на других КЭ. Таким образом, имеется возможность создания каталога разнообразных КЭ с произвольными значениями локальной аппроксимирующей функции.

В энергетическом смысле МКЭ может быть интерпретирован как развитие метода Ритца. Одной из главных трудностей применения метода Ритца к сложным конструкциям является выбор аппроксимирующих функций для всего тела. Однако, если разбить исследуемую конструкцию на ряд подобных областей, например, однородное тело можно разбить на ряд отрезков, двумерные тела – на ряд прямоугольников или треугольников, трехмерные тела – на ряд тетраэдров, конструкции – на ряд балок и пластин, то аппроксимирующие функции для каждого элемента легко выбрать. Подобная операция и производится в МКЭ.

Дискретизация судовых конструкций

Основывается на представлении конструкции в виде ансамбля элементов конечных размеров с известными геометрическими и упругими характеристиками, взаимодействующими между собой в конечном числе узловых точек. В этих узлах со стороны элементов прикладывают некоторые условные усилия взаимодействия, характеризующие действие распределенных внутренних напряжений, приложенных вдоль границы стыковки смежных элементов.

Пример. Пространственные ферменные конструкции.

Состоят из прямолинейных шарнирно-сочлененных стержней. Каждый стержень работает только на растяжение-сжатие.

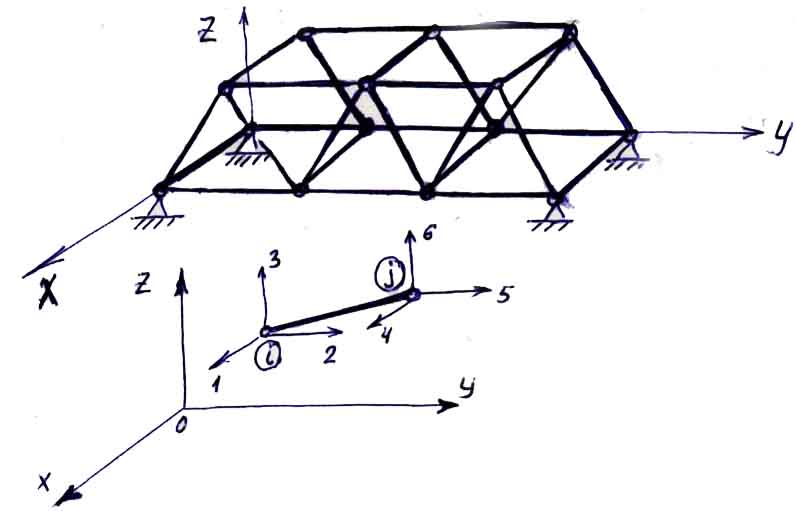
симметрично

–матрица усилий

Пример. Плоские балочные конструкции.

В этом случае стержни конструкции, сходящиеся в одном узле, жестко скреплены друг с другом. Поэтому наряду с осевыми усилиями, появятся перерезывающие силы и изгибающие моменты. Примером таких конструкций является шпангоутная рама.

=
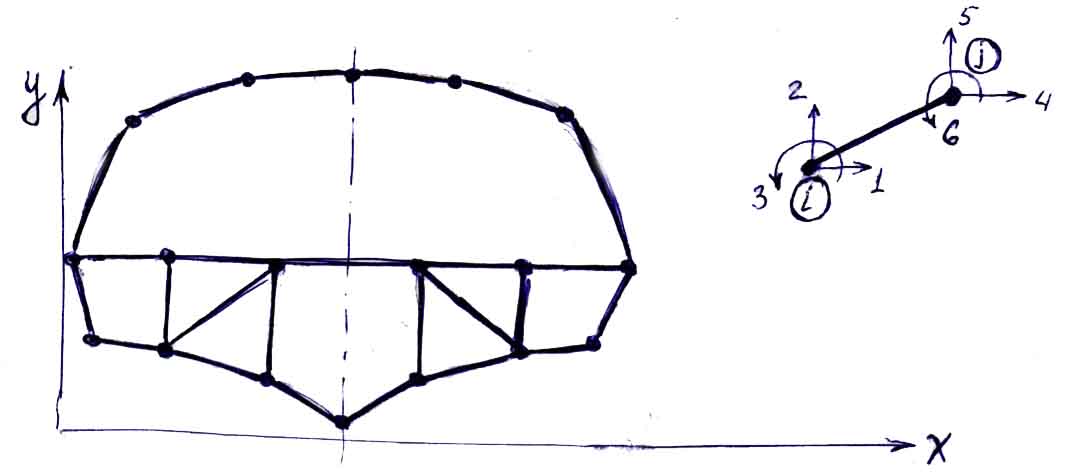
симметрично

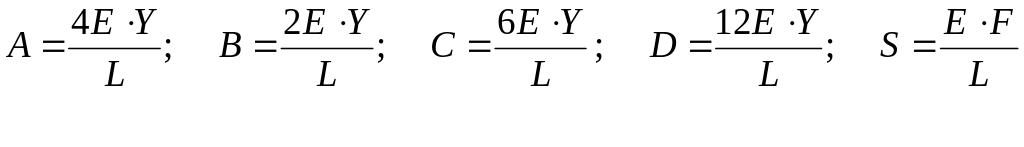
			0			0
			0			0

– матрица усилий балочного элемента

Пример. Плоская задача теории упругости. Для ее решения применяются треугольные и прямоугольные конечные элементы. С помощью этих элементов решается широкий круг задач: концентрация напряжений в пластинах, расчет широкополых балок, выбор присоединенного пояска, расчет шпангоутных рам, объемных отсеков судовых корпусов, расчет судовых перекрытий со вторым дном.

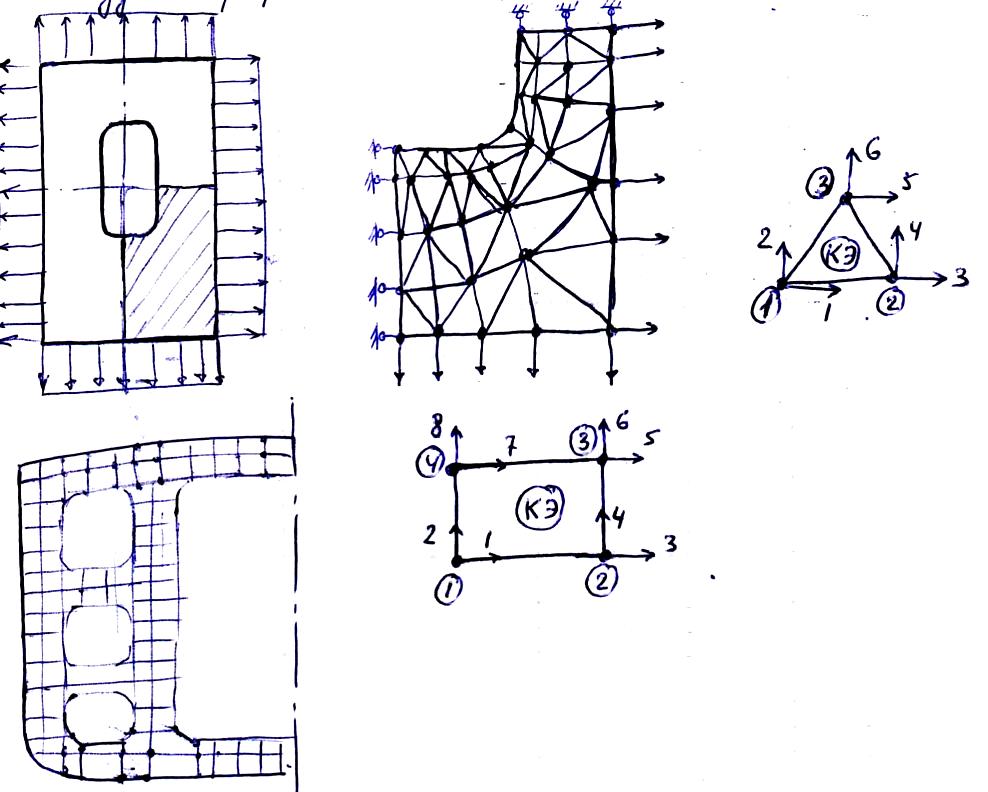
Пример. Судовой корпус представляет конструкцию, состоящую из пластин и подкрепляющих их ребер. Поэтому дискретная модель судового корпуса может быть представлена в виде ансамбля стержневых (соответствующих продольному и поперечному набору) и пластинчатых (соответствующих обшивке) элементов.

При этом уже нет необходимости рассматривать раздельно общую прочность (эквивалентный брус) и местную прочность (перекрытия, шпангоутные рамы, пластины). Весь ансамбль КЭ рассматривается как единое целое, что соответствует (моделирует) рабочие конструкции как единое целое.

Замена исходной конструкции совокупностью КЭ подразумевает равенство энергии конструкции и ее дискретной модели. Для некоторых конструкций соблюдение энергетического баланса ведет к получению дискретной модели, точно описывающей поведение исходной конструкции. Это характерно для конструкций, которые состоят из отдельных элементов с дискретным сочленением их между собой. В качестве примера можно указать на фермы, рамы, стержневые системы. Если же элементы реальной конструкции имеют вдоль своей границы непрерывные связи со смежными элементами, то при построении дискретной модели делаются априорные предположения о характере силового или кинематического взаимодействия между смежными элементами. В этом случае дискретная модель будет лишь приближенно отражать поведение исходной конструкции.

При разработке дискретной модели исходят из следующих соображений:

1. Необходимой точности получаемых результатов;

2. Наличия имеющихся вычислительных средств, их мощности и соответствующего математического обеспечения;

3. Наличия в каталоге конечных элементов матриц жесткости, нужного для расчета КЭ.

Выше был описан процесс физической дискретизации конструкций (в отличие от математической). При этом уже сама идеализация, приводящая исходную конструкцию к совокупности КЭ, связанных между собой лишь в узловых точках, требует чтобы напряженно-деформированное состояние в каждом из элементов однозначно определялось через значения его узловых перемещений (метод перемещений) или через значения его узловых усилий (метод сил). Однако метод перемещений при расчете сложных конструкций дает численные процедуры более простые и стандартные, чем метод сил, а с этим связана простота алгоритмизации, программирования и большая универсальность МКЭ в форме метода перемещений. Это предопределило преимущественное использование в расчетной практике метода перемещений.

Значение коэффициентов матрицы жесткости элемента зависят от геометрических и жесткостных параметров КЭ, а также от принятого закона изменения компонентов перемещений (или напряжений). При этом выбор выражений, аппроксимирующих характер изменения перемещений (напряжений) по объему КЭ, является одним из ответственных моментов в общей процедуре МКЭ. Всегда желательно, чтобы этот выбор приводил к удовлетворению уравнений совместности деформаций внутри объема КЭ, к отсутствию разрывов в компонентах перемещений и напряжений вдоль линий стыковки смежных элементов. Ограниченность числа степеней свободы для КЭ не позволяет удовлетворить всем этим условиям, а следовательно, и получить точное решение. Поэтому при использовании того или иного конечно-элементного пакета желательно иметь представление о возможностях КЭ и необходимо протестировать его на простейших примерах, где имеется точное решение.