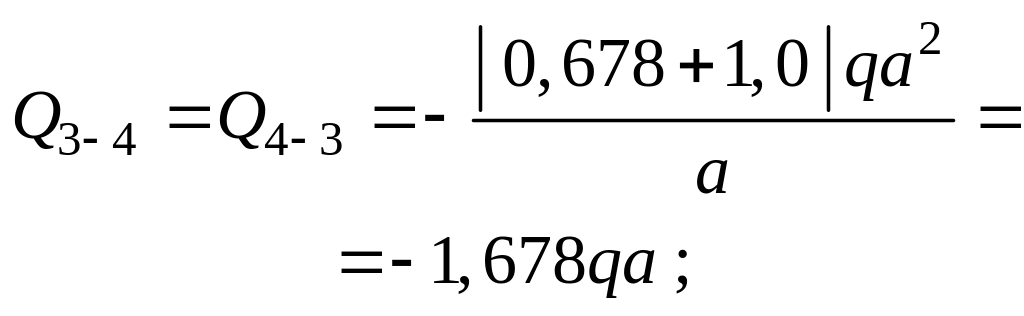4.6. Решение канонической системы уравнений.
Решение полученной системы линейных алгебраических уравнений (3.4) выполним методом подстановки, который заключается в следующем:
Одно из уравнений системы (3.4), например, 1-ое уравнение, преобразуем к виду, в котором неизвестная выражена через :
.
Полученное выражение подставляем вместо во 2-ое уравнение системы (3.4) и находим значение :
.
Воспользовавшись выражением через , записанным в пункте а), найдем соответствующее значение :
.
Проверка правильности решения канонической системы уравнений:
Подставим найденные значения и в каждое из уравнений системы (3.4) и проверим, получаются ли тождества. В противном случае, необходимо произвести проверку вычислений, выполненных в ходе решения канонической системы уравнений, на наличие ошибок.
Наличие незначительных погрешностей, выявленных в ходе проверки, объясняется тем, что вычисления в примере проводились в десятичных дробях, округленных до 3-х значащих цифр после запятой.
Таким образом, решение системы уравнений (3.4) можно записать в следующем виде:
.
4.7. Матричная форма эпюры изгибающих моментов в заданной расчетной схеме.
Построение эпюры изгибающих моментов в ЗРС производится по формуле:
|
(3.5) |
.Проведем вычисления по формуле (3.5):
.
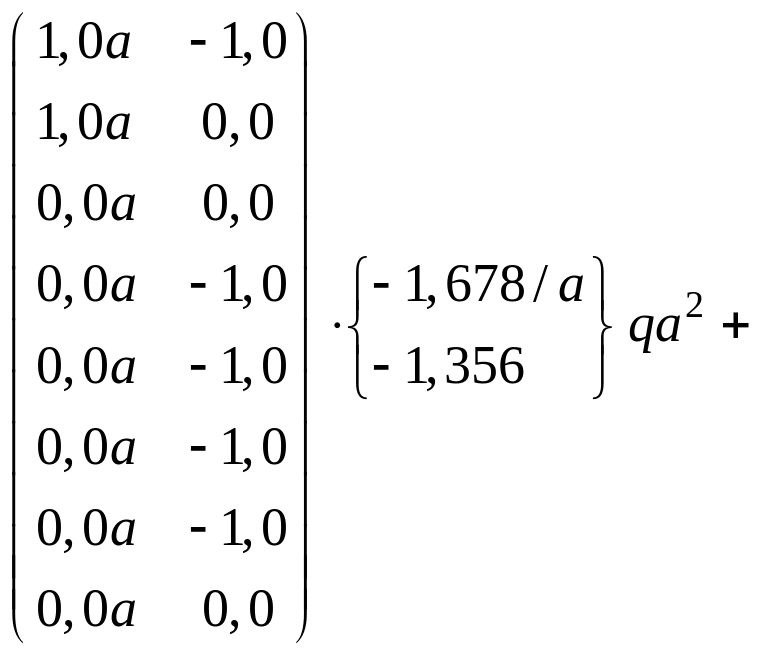
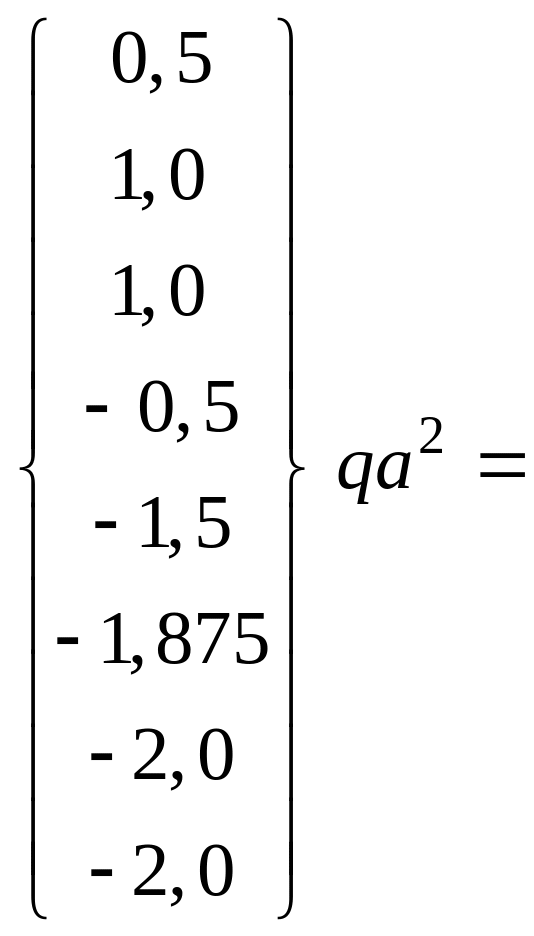
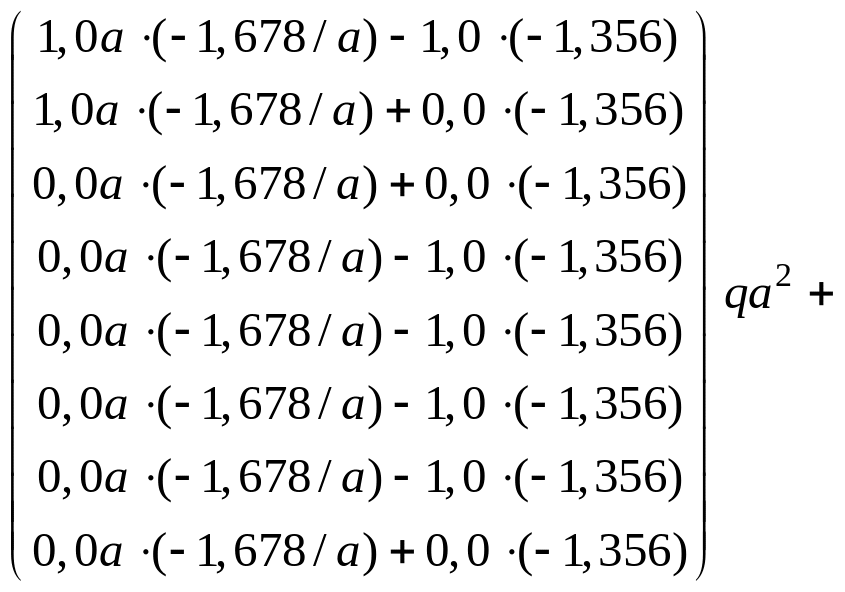
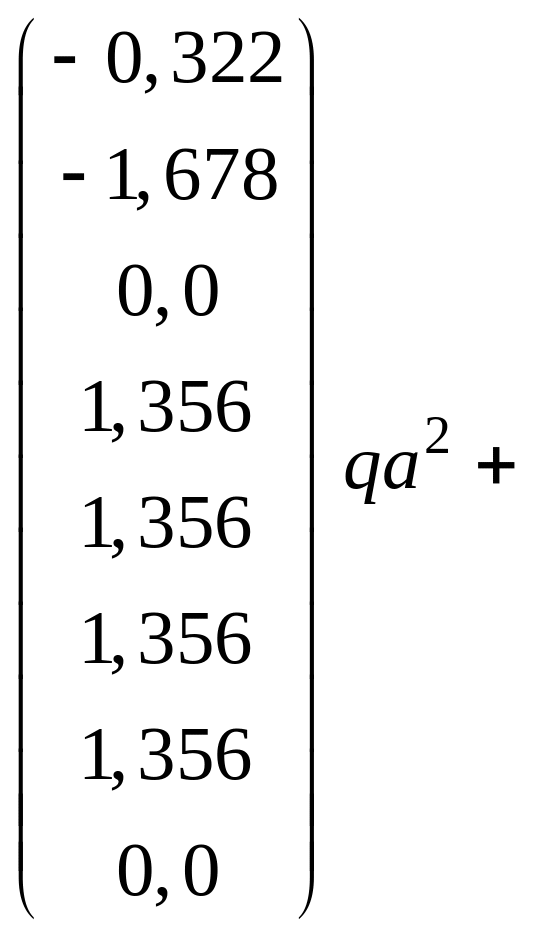
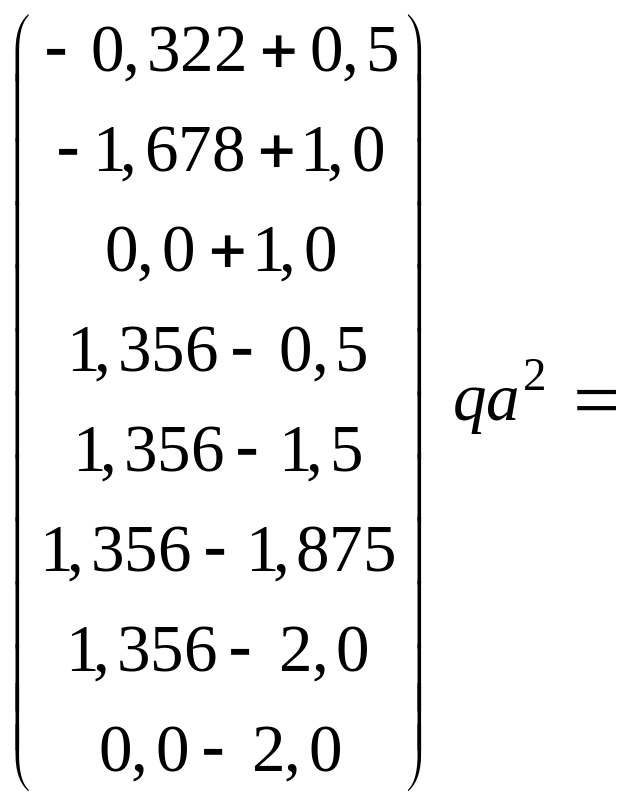
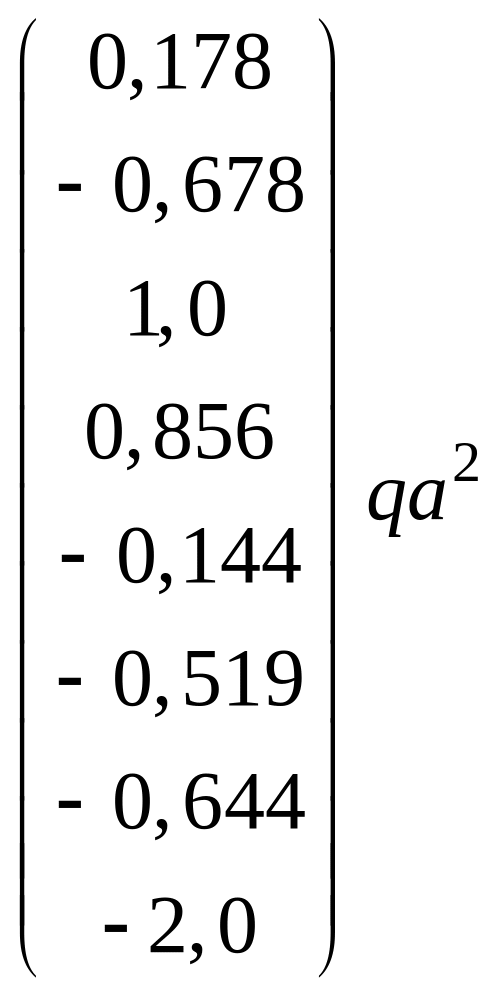Итак, мы получили решение задачи об
определении распределения изгибающих
моментов в заданном статически
неопределимом ломаном брусе методом
сил в матричной форме. Элементы матрицы
вычислены с тремя значащими цифрами.
5. Построение эпюр усилий в заданной расчетной схеме
5.1. Построение окончательной эпюры изгибающих моментов.
Эпюра изгибающих моментов в ЗРС, которая называется также «окончательной» эпюрой изгибающих моментов, представлена матрицей .
Построение эпюры изгибающих моментов в ЗРС по полученной матрице значений проводится с учетом следующих факторов:
сечений и правила знаков, введенных на схеме дискретизации (рис. 3.21);
нулевых значений изгибающего момента в сечениях 1 и 11 (см. п. 4.4.1);
равенства значений изгибающего момента в сечениях 6 и 7 (см. п. 4.4.2).
характера изменения изгибающего момента на участках между контролируемыми сечениями (линейный или параболический).
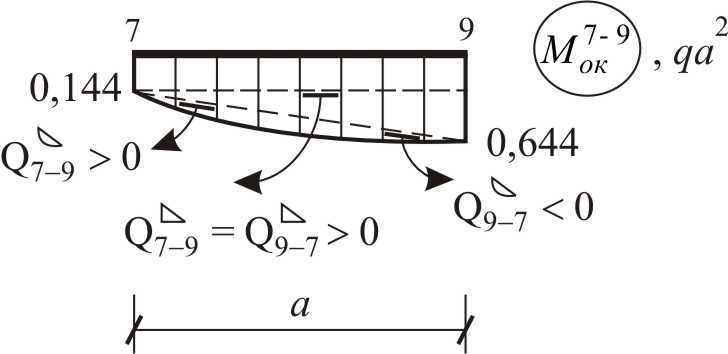
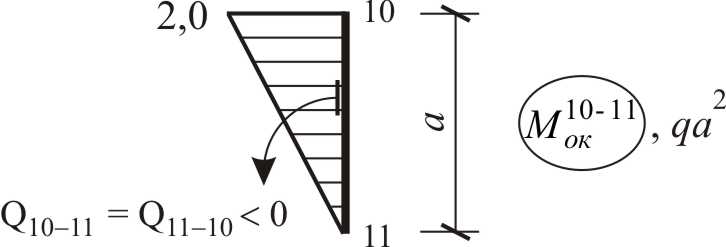
На рис. 28 показан результат построения по матрице окончательной эпюры изгибающих моментов в ЗРС с учетом сформулированных выше правил.
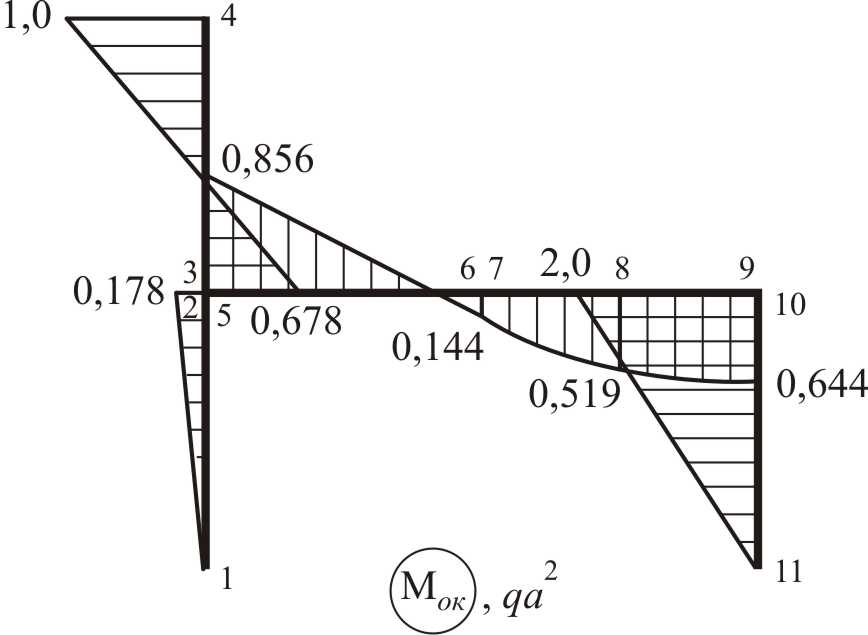
Рис. 3.22
5.2. Построение эпюры поперечных сил.
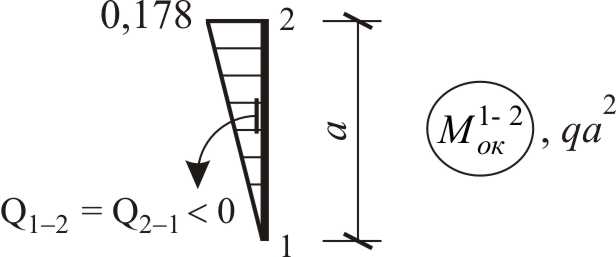
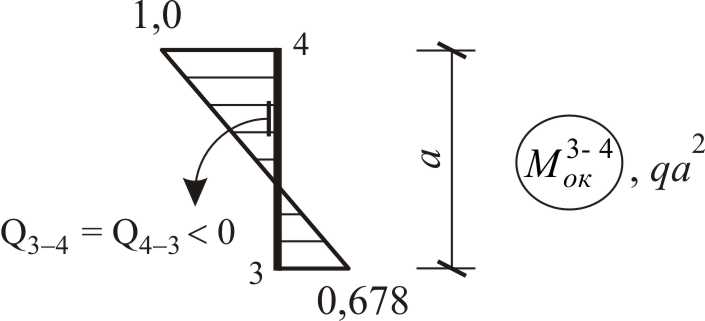
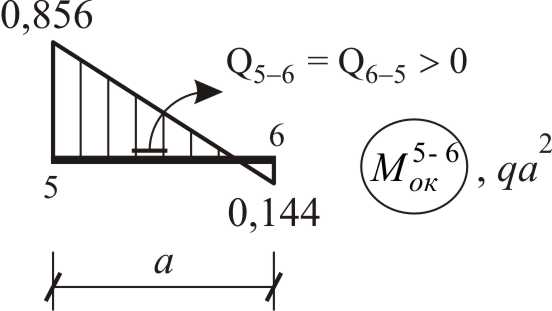
Найдем значения поперечных усилий на концах участков, вдоль которых закон изменения изгибающего момента не меняет своего математического вида, используя способ графического дифференцирования (см. рис. 3.23).
|
|
|
Рис. 3.23 (начало) |
|
|
|
|
|
Рис. 3.23 (окончание) |
;
;
;
;
.
По результатам вычислений (рис. 3.23) построена эпюра поперечных сил, изображенная на рис. 3.24.
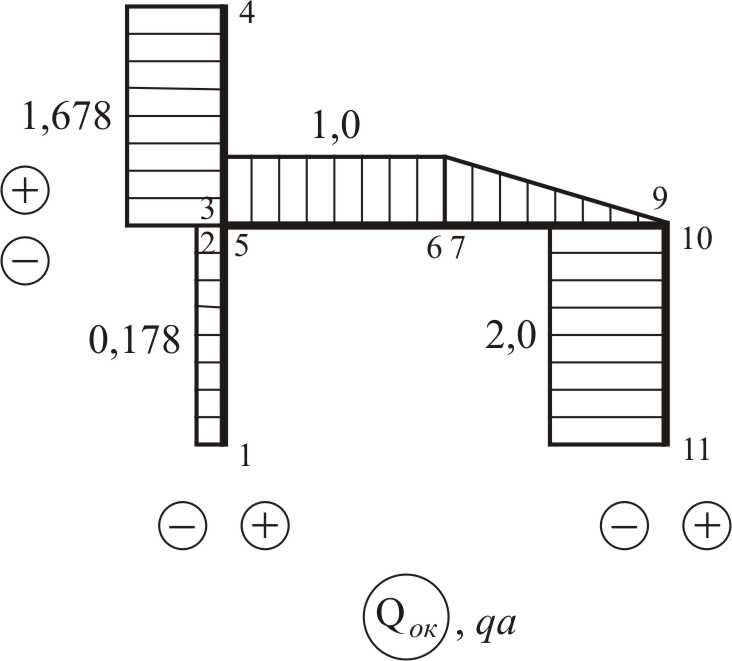
Рис. 3.24