31.Начальные и центральные моменты непрерывной случайно величины

Начальным моментом порядка   случайной величины  называют математическое ожидание величины  : .

Центральным моментом порядка   случайной величины   называют математическое ожидание величины  :

.

Начальный момент первого порядка   равен математическому ожиданию самой случайной величины  .

Центральный момент первого порядка равен нулю: .

Центральный момент второго порядка представляет собой дисперсию случайной величины  :

.

32.Биноминальный з-н распределения

Дискретная случайная величина х имеет биноминальный закон распределения с параметрами n и p, если она принимает значения 0,1,2…,m,…,n с вероятностями P(x=m)=c_n^mp^mq^n-m

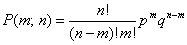
M(x)=np

D(x)=npq

33.З-н распределения Пуассона

Дискретная случайная величина х имеет з-н распределения Пуассона с параметрами λ>0, если она принимает значения 0,1,2,…,m(беск, но счётное число раз).

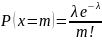
M(x)= λ

D(x)= λ

34.Геометрическое распределение.

Дискретная случайная величина х имеет геом. распр. с параметром p,если она принимает значения 1,2,3….,m(бесконечное число раз) с вероятностями

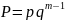
p=const

35.Равномерное распределение

Непрерывная случайная величина имеет з-н распределения на отрезке от а до b, если её плотность вероятности 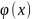постоянна на этом отрезке и равна 0 вне его

F(x)=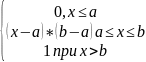

M(x)=

D(x)=

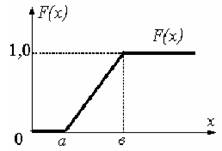
36. Показательный закон

Показательным (экспоненциальным) называют распределение вероятностей непрерывной случайной величины X, которое описывается плотностью

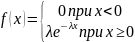
где λ − постоянная положительная величина.

Функция распределения показательного закона

Вероятность попадания в интервал (a, b) непрерывной случайной величины X, распределенной по показательному закону,

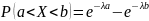
Математическое ожидание, дисперсия и среднее квадратическое отклонение показательного распределения соответственно равны:

M(X) = 1/λ, D(X) = 1/λ², σ(X) = 1/λ

Таким образом, математическое ожидание и среднее квадратическое отклонение показательного распределения равны между собой.

37. Нормальное распределение

Нормальным называют распределение вероятностей непрерывной случайной величины X, плотность которого имеет вид

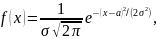
где a — математическое ожидание, σ — среднее квадратическое отклонение X.

Вероятность того, что X примет значение, принадлежащее интервалу (α, β).

где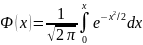 − функция Лапласа.

Вероятность того, что абсолютная величина отклонения меньше положительного числа δ,

P(|X-a| ˂ δ) = 2Ф(δ/σ).

При а = 0 справедливо равенство

P(|X|<δ) = 2Ф(δ/σ).

Асимметрия, эксцесс, мода и медиана нормального распределения соответственно равны:

A_s = 0, E_k = 0, M₀ = a, M_e = a, где a = M(X).

38. Свойства случайной величины, распеделенной по нормальному закону

1. Вероятность попадания случайной величины X, распределенной по нормальному закону, в интервал [x₁, x₂], равна

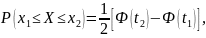
где

2. Вероятность того, что отклонение случайной величины X, распределенной по нормальному закону, от математического ожидания a не превысит величину ∆ > 0 (по абсолютной величине), равна

P(|X-a| ≤ ∆) = Ф(t).

3. «Правило трех сигм»

Если случайная величина X имеет нормальный закон распределения с параметрами а и σ², т. е. N(a; σ²), то практически достоверно, что ее значения заключены в интервале (a-3σ, a+3σ).