- •Поле, образованное бесконечно длинным заряженным цилиндром
- •Поле, образованное заряженной сферической поверхностью
- •6). Поле объемного заряженного шара
- •Поле, образованное двумя разноименными заряженными плоскостями (бесконечно большими)
- •8.Теорема Гаусса в дифференциальной форме.
- •9. Работа сил электростатического поля. Потенциал электрического поля.
- •10. Связь между напряженностью электрического поля и потенциалом. (градиент)Эквипотенциальные поверхности.
- •11. Проводники в электростатическом поле
- •12.Электроемкость.
- •22. Закон Ома для неоднородного участка цепи.
- •23. Закон Ома для неоднородного участка цепи
- •1. Алгебраическая сумма токов, сходящихся в узле, равна нулю.
Электрический заряд и его свойства.
Электрический заряд одна из основных первичных характеристик частицы.
Фундаментальные свойства заряда:
1)электрический заряд существует в двух видах: как положительный, так и отрицательный;
2)в любой электрически изолированной системе алгебраическая сумма зарядов не изменяется –– закон сохранения электрического заряда;
3)электрический заряд является релятивистски инвариантным: его величина не зависит от системы отсчета, а значит, не зависит от того, движется он или покоится.
Точечным зарядом называется заряженное тело, размерами которого можно пренебречь по сравнению с расстояниями от этого тела до других тел, несущих электрический заряд.
2.Закон Кулона. Напряжённость электрического поля. Поток силовых линий напряжённости.
З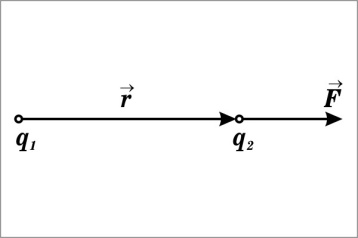 акон
Кулона:
сила взаимодействия двух точечных
зарядов пропорциональна величине
каждого из зарядов и обратно пропорциональна
квадрату расстояния между ними.
акон
Кулона:
сила взаимодействия двух точечных
зарядов пропорциональна величине
каждого из зарядов и обратно пропорциональна
квадрату расстояния между ними.
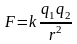 где
k
— коэффициент пропорциональности
где
k
— коэффициент пропорциональности
Закон
Кулона в векторной форме:
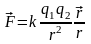 .
Под
r
следует подразумевать
вектор,
проведенный к тому из зарядов, к которому
приложена сила.
.
Под
r
следует подразумевать
вектор,
проведенный к тому из зарядов, к которому
приложена сила.
Коэффициент
пропорциональности в законе Кулона
полагают равным
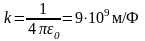 .
.
Электрическое поле. Напряженность поля
Взаимодействие между зарядами осуществляется через электрическое поле. Всякий заряд изменяет свойства окружающего его пространства — создает в нем электрическое поле. Это поле проявляет себя в том, что помещенный в какую-либо его точку электрический заряд оказывается под действием силы.
В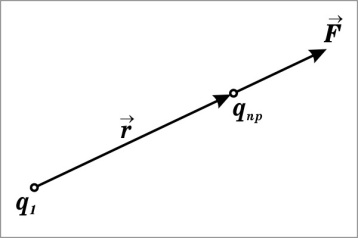 екторную
величину
екторную
величину
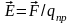 называют
напряженностью электрического поля в
данной точке. Она численно равна силе,
действующей на единичный точечный
заряд, находящийся в данной точке поля.
Направление вектора Е
совпадает с направлением силы, действующей
на положительный заряд.
называют
напряженностью электрического поля в
данной точке. Она численно равна силе,
действующей на единичный точечный
заряд, находящийся в данной точке поля.
Направление вектора Е
совпадает с направлением силы, действующей
на положительный заряд.
Напряженность
поля точечного заряда
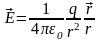 ;
;
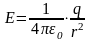 ;
;
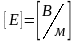 .
.
Линии напряженности для точечного заряда:
Л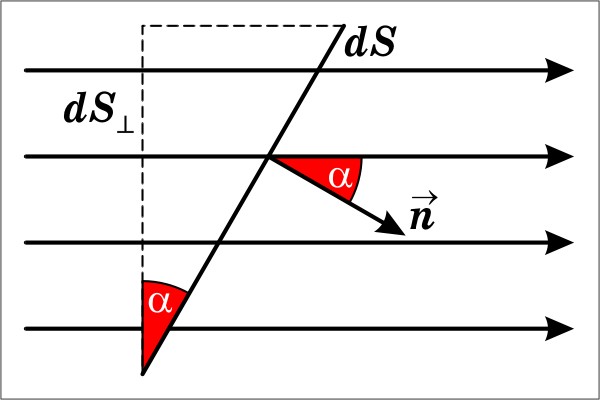 инии
напряженности начинаются на положительных
зарядах и уходят в бесконечность, или
приходят из бесконечности и заканчиваются
на отрицательных зарядах. Это свойство
линии Е
является
общим для всех электростатических
полей.
инии
напряженности начинаются на положительных
зарядах и уходят в бесконечность, или
приходят из бесконечности и заканчиваются
на отрицательных зарядах. Это свойство
линии Е
является
общим для всех электростатических
полей.
Число
линий, пронизывающих площадку
 :
:

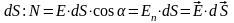 ,
где En
– проекция Е
на
направление нормали.
,
где En
– проекция Е
на
направление нормали.
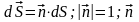 -
единичный вектор нормали.
-
единичный вектор нормали.
Поток
вектора E
через поверхность S:

Поле диполя
Диполь-система 2х q равн по величине но разные по знакам,размнож на расстояние
Ql=p- момент диполя (направление к положит заряду)
E=1/r3
Е поля диполя уменьш пропорционально кубу расстояния на продолжении оси.
Е=р/4DEr3
Напряжённсть поля диполя в направлении перпендик к центру оси диполя изм к центру обратно пропорц-но кубу расстояния
Теорема Гаусса и её док-во.
Теорема
Гаусса:
поток вектора Е
сквозь замкнутую поверхность равен
алгебраической сумме зарядов внутри
этой поверхности, деленной на ε0:
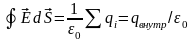
Доказательство:
1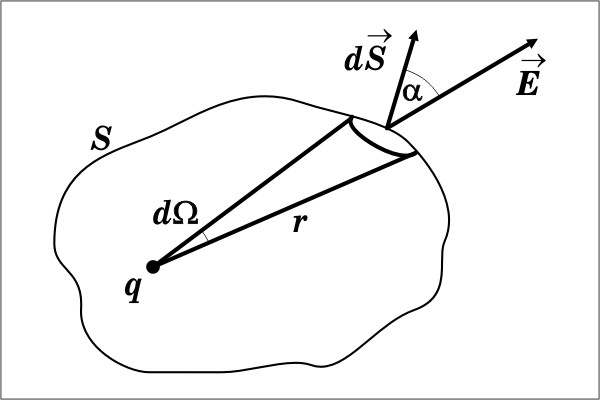 .
Для одного точечного заряда:
.
Для одного точечного заряда:
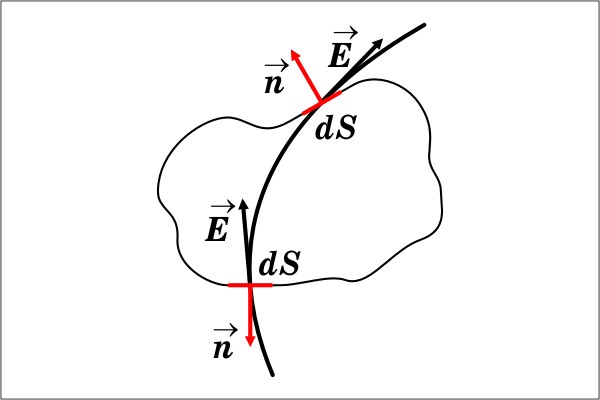
Поток вектора Е через площадку dS:

Поток через всю замкнутую поверхность S:
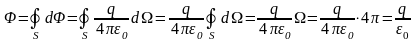
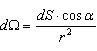 -
телесный угол, опирающийся на dS
-
телесный угол, опирающийся на dS
Для
одного заряда:
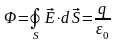
2. Поверхность имеет сложную форму:

Какова бы ни была форма замкнутой поверхности, охватывающей точечный заряд q, поток вектора Е сквозь эту поверхность оказывается равным q/ε0.
3.
Поле, созданное системой зарядов
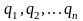 :
:
Согласно
принципу суперпозиции
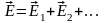
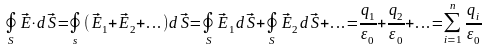
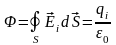
4. Заряды располагаются вне поверхности:
Е сли
внутри поверхности заряды отсутствуют,
поток равен нулю. Вклад, вносимый в поток
каждой линией равен нулю, так как каждая
линия пересекает поверхность четное
число раз.
сли
внутри поверхности заряды отсутствуют,
поток равен нулю. Вклад, вносимый в поток
каждой линией равен нулю, так как каждая
линия пересекает поверхность четное
число раз.
Если
заряд распределен внутри замкнутой
поверхности непрерывно с объемной
плотностью
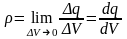 (Δq
заряд внутри малого объема ΔV),
теорема Гаусса должна быть записана
следующим образом:
(Δq
заряд внутри малого объема ΔV),
теорема Гаусса должна быть записана
следующим образом:
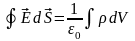 .Интеграл
справа берется по объему V,
охватываемому поверхностью S.
Важная
особенность.
Поле Е
зависит от конфигурации зарядов, а поток
вектора Е
сквозь произвольную замкнутую поверхность
S
определяется только алгебраической
суммой зарядов внутри поверхности S.
Если передвинуть заряды, без пересечения
поверхности S,
то поток вектора Е
через эту поверхность останется прежним,
хотя само поле Е может измениться, причем
весьма существенно.
.Интеграл
справа берется по объему V,
охватываемому поверхностью S.
Важная
особенность.
Поле Е
зависит от конфигурации зарядов, а поток
вектора Е
сквозь произвольную замкнутую поверхность
S
определяется только алгебраической
суммой зарядов внутри поверхности S.
Если передвинуть заряды, без пересечения
поверхности S,
то поток вектора Е
через эту поверхность останется прежним,
хотя само поле Е может измениться, причем
весьма существенно.
5. Применение теоремы Гаусса для расчета напряженности электрического поля. Поле заряженной плоскости и двух плоскостей.
П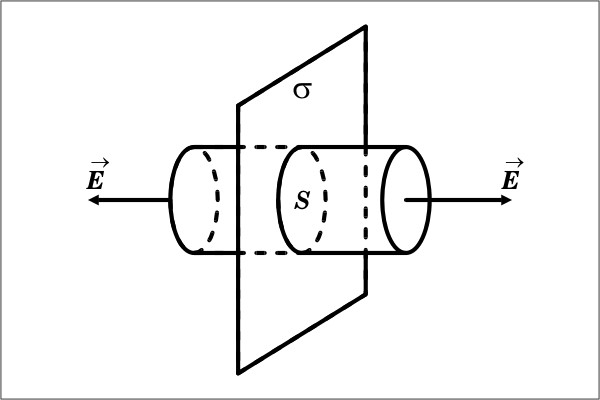 ример
1. Поле
равномерно заряженной плоскости.
ример
1. Поле
равномерно заряженной плоскости.
Поверхностная
плотность заряда

1. Т.к. плоскость бесконечна, то вектор напряженности в любой точке будет перпендикулярен этой плоскости.
2.
Модуль
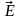 будет одинаковым, если взять точку,
которая находится на одинаковом
расстоянии.
будет одинаковым, если взять точку,
которая находится на одинаковом
расстоянии.
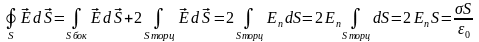

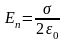
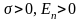 -
вектор E
направлен от плоскости.
-
вектор E
направлен от плоскости.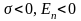 -
вектор E
направлен к заряженной плоскости.
-
вектор E
направлен к заряженной плоскости.
Пример 2. Поле двух параллельных плоскостей, заряженных равномерно разноименными зарядами с плотностями +σ и -σ.
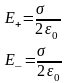
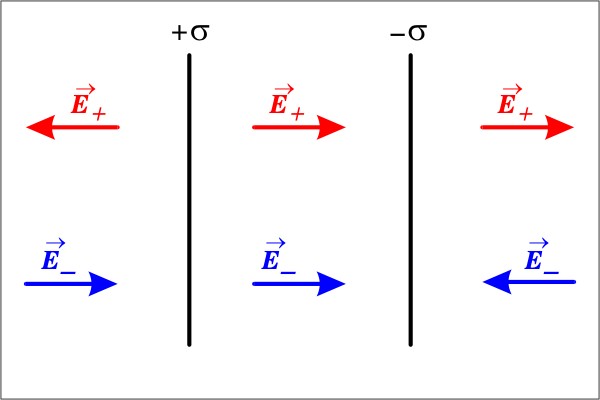
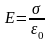 -
поле сосредоточено между плоскостями
и является однородным.
-
поле сосредоточено между плоскостями
и является однородным.
Поле, образованное бесконечно длинным заряженным цилиндром
Р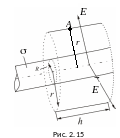 ассчитаем
напряженность поля, создаваемого
бесконечно длинным цилиндром радиуса
R,
заряженным с поверхностной плотностью
ассчитаем
напряженность поля, создаваемого
бесконечно длинным цилиндром радиуса
R,
заряженным с поверхностной плотностью
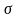 в точке А,
отстоящей на расстояния r
от оси цилиндра. Из соображений симметрии
следует, что напряженность в любой точке
направлена вдоль радиальной прямой,
перпендикулярной к оси цилиндра, а
значение напряженности зависит лишь
от расстояния r
от цилиндра.
в точке А,
отстоящей на расстояния r
от оси цилиндра. Из соображений симметрии
следует, что напряженность в любой точке
направлена вдоль радиальной прямой,
перпендикулярной к оси цилиндра, а
значение напряженности зависит лишь
от расстояния r
от цилиндра.
Вырежем
из бесконечно длинного цилиндра элемент
длиной h.
Окружим этот элемент цилиндрической
поверхностью (коаксиальной с заряженной)
радиуса r,
так, чтобы эта поверхность проходила
через точку А
(рис. 2.15). Для оснований внешнего
цилиндра
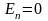 ,
для боковой поверхности (заряд считаем
положительным)
,
для боковой поверхности (заряд считаем
положительным)
 .
Силовые линии поля пересекают только
боковую поверхность цилиндра радиуса
r.
Следовательно, поток вектора
через эту замкнутую поверхность будет
равен
.
Силовые линии поля пересекают только
боковую поверхность цилиндра радиуса
r.
Следовательно, поток вектора
через эту замкнутую поверхность будет
равен
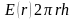 .
Если
.
Если
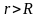 внутрь поверхности попадает заряд
внутрь поверхности попадает заряд
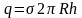 ,
где
–поверхностная
плотность заряда. Применяя теорему
Гаусса, получаем:
,
где
–поверхностная
плотность заряда. Применяя теорему
Гаусса, получаем:
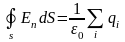 ,
,
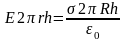 ,
откуда
,
откуда
 . (5)
. (5)
Если
 ,
рассматриваемая замкнутая поверхность
не содержит внутри зарядов, вследствие
чего
,
рассматриваемая замкнутая поверхность
не содержит внутри зарядов, вследствие
чего
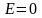 .
Таким образом, внутри заряженной
цилиндрической поверхности поле
отсутствует.
.
Таким образом, внутри заряженной
цилиндрической поверхности поле
отсутствует.
Если
радиус цилиндра
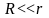 ,
а заряд распределяется по длине цилиндра
с линейной плотностью τ. Тогда можно
формулу (17) преобразовать:
,
а заряд распределяется по длине цилиндра
с линейной плотностью τ. Тогда можно
формулу (17) преобразовать:
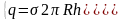

Т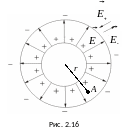 огда
огда
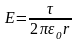 (6)
(6)
Поле, образованное заряженной сферической поверхностью
Р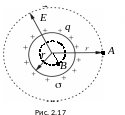 ассмотрим
поле, создаваемое сферической поверхностью
радиуса R,
заряженной с постоянной поверхностной
плотностью
.
Это поле обладает центральной симметрией.
Это означает, что направление вектора
в любой точке проходит через центр
сферы, а значение напряженности является
функцией расстояния r
от центра сферы (рис. 2.
ассмотрим
поле, создаваемое сферической поверхностью
радиуса R,
заряженной с постоянной поверхностной
плотностью
.
Это поле обладает центральной симметрией.
Это означает, что направление вектора
в любой точке проходит через центр
сферы, а значение напряженности является
функцией расстояния r
от центра сферы (рис. 2.
Найдем напряженность поля, созданную заряженной сферой в точках А и В. Через точки А и В проведем сферические поверхности и найдем поток вектора напряженности через эти поверхности.
Точка В находится внутри заряженной сферической поверхности, на расстоянии r от центра (r<R). Сферическая поверхность, проведенная через эту точку, не будет содержать внутри заряда. Следовательно, по теореме Гаусса , напряженность в точке В будет равна нулю. Е=0 (r<R) (рис. 2.17).
Найдем напряженность поля, созданного заряженной сферической поверхностью в точке А, находящейся на расстоянии r от центра сферы. Окружим заряженное тело замкнутой сферической поверхностью, радиуса r, проходящей через точку А (рис. 2.17).
Для
всех точек этой поверхности
.
Внутрь поверхности попадает весь заряд
q,
создающий рассматриваемое поле.
Следовательно,
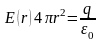 (так как
(так как
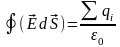 ).
).
Таким образом, напряженность поля в точках, расположенных на расстоянии r>R, равна
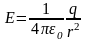 (8)
(8)
Поле
вне заряженной сферической поверхности
имеет такой же вид, как поле точечного
заряда q,
находящегося на расстоянии r
от точки А.
Если известна поверхностная плотность
заряда σ, то
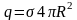 ,
подставив в (8), получим
,
подставив в (8), получим
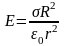 . (9)
. (9)
6). Поле объемного заряженного шара
Найдем напряженность поля, созданного заряженным шаром в точке А, находящейся на расстоянии r от центра шара. Окружим заряженное тело замкнутой сферической поверхностью, радиуса r, проходящей
через точку А (рис. 2.18).
Для всех точек этой поверхности . Внутрь поверхности попадает весь заряд q, создающий рассматриваемое поле. Следовательно, (так как ). Таким образом, для поля вне шара радиусом R (рисунок 2.18) получается тот же результат, что и для сферы, т.е. справедлива формула:
 .
.
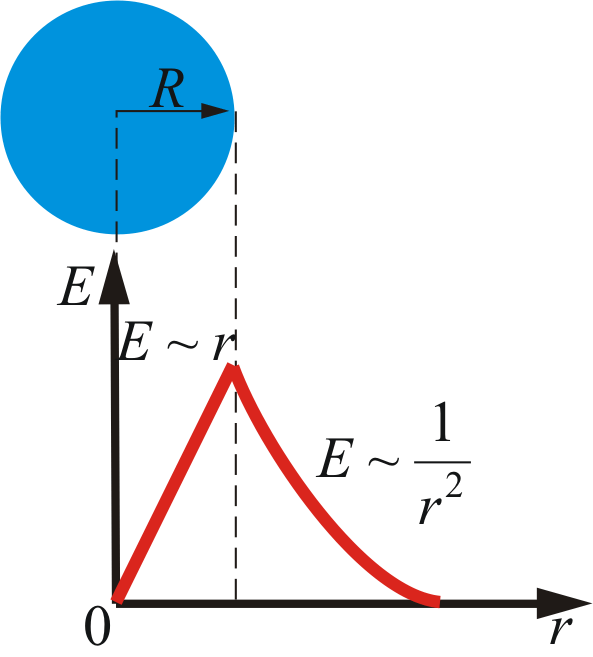
Точка В находится внутри заряженной сферической поверхности, на расстоянии r от центра (r<R). Сферическая поверхность, проведенная через эту точку содержать в себе заряд, равный
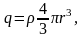
где
ρ – объемная плотность заряда, равная
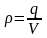 ;
;
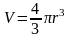 – объем шара. Тогда по теореме
Остроградского-Гаусса
запишем:
– объем шара. Тогда по теореме
Остроградского-Гаусса
запишем:
 ,
,
т.е. внутри шара
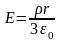 . (10)
. (10)
Таким
образом, внутри шара напряженность поля
пропорциональна расстоянию от центра
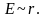
6. Применение теоремы Гаусса для расчета напряженности электрического поля Поле бесконечного круглого цилиндра.
Пример
3. Поле
бесконечного круглого цилиндра,
заряженного равномерно по поверхности
так, что на единицу его длины приходится
заряд

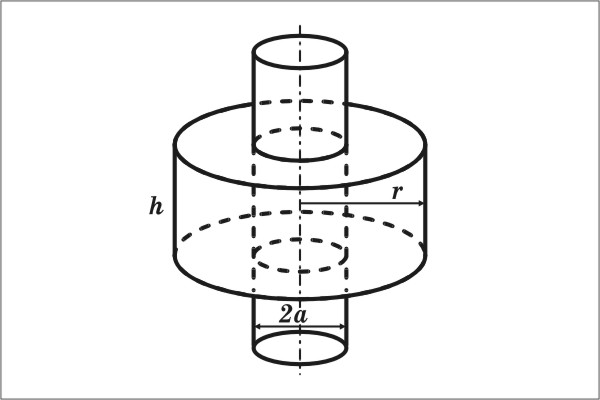
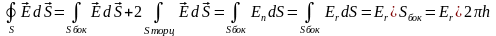
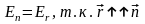
1.
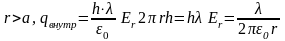
2.