
- •1 Электрический заряд и его свойства. Законы сохранения и квантования заряда. Взаимодействия зарядов. Закон Кулона. Характеристики неточечных зарядов.
- •2.Электрическое поле, его характеристики- напряженность, индукция и потенциал. Графическое изображение полей. Поле точечного заряда. Сложение электрических полей.
- •3.Метод вычисления напряженности. Применение принципа суперпозиции для вычисления электрических полей неточечных зарядов. Напряжённость электрического поля точечного заряда
- •4.Поток напряженности электрического поля. Теорема Остроградского-Гаусса. Примеры применения теоремы Гаусса для расчета электрических полей.
- •Циркуляция вектора напряженности
- •6.Связь между напряженностью эл. Поля и потенциалом. Градиент потенциала. Вычисление потенциала для неточечных зарядов.
- •7.Микроскопическое строение диэлектрика. Жесткий и мягкий диполь в электрическом поле.
- •8.Поляризация диэлектрика. Вектор поляризации, диэлектрическая восприимчивость. Поверхностные связанные заряды.
- •9.Электрическое поле в диэлектрике. Физический смысл относительной диэлектрической проницаемости. (Связь векторов поляризации, напряженности и индукции).
- •10.Сегнетоэлектрики, диэлектрический гистерезис, домены. Пьезоэлектрический эффект.
- •11.Проводники. Условия равновесия зарядов в проводнике. Распределение избыточных неподвижных зарядов в проводнике.
- •Равновесное распределение зарядов на проводниках.
- •12.Проводники во внешнем электрическом поле. Возникновение наведенного заряда на проводнике.
- •13.Электроемкость. Емкость шара. Заземление. Емкость конденсатора, системы конденсаторов.
- •14. Энергия системы точечных зарядов. Энергия заряженного проводника. Энергия эл. Поля. Плотность энергии эл. Поля.
- •15.Постоянный электрический ток. Основные понятия: сила тока, эдс, напряжение, разность потенциалов, сопротивление проводника и полупроводника.
- •]Эдс индукции
- •Электрический ток в полупроводниках
- •16.Закон Ома в интегральной форме для однородного и неоднородного участков и замкнутой цепи. Закон Ома в дифференциальной форме .
- •2.3 Законы Ома в интегральной форме
- •2.3.1 Закон Ома в дифференциальной форме
- •18. Классическая электронная теория электропроводности. Вывод закона Ома.
- •19.Вывод закона Джоуля-Ленца. Недостатки классической теории.
- •20. Правила Кирхгофа. Их применение в расчета сопротивления проводников. Первый закон
- •Второй закон
- •21. Магнитное поле. Вектор магнитной индукции. Напряженность магнитного поля. Закон Био-Савара-Лапласса.
- •22.Применение закона Био-Савара-Лапласса для расчета индукции магнитного поля прямого тока.
- •23.Применение закона Био-Савара-Лапласса для расчета индукции магнитного поля в центре на оси кругового тока. Магнитный момент кругового тока.
- •24. Закон Ампера. Взаимодействие прямых длинных параллельных токов.
- •Два параллельных проводника
- •25.Магнитный диполь. Поведение магнитного диполя в однородном и неоднородном магнитном поле.
- •26.Вихревой характер магнитного поля. Закон полного тока, его применение для расчета магнитного поля соленоида и тороида. Вихревой характер магнитного поля
- •27. Магнитный поток. Теорема Гаусса для магнитного поля. Работа, совершаемая при перемещение проводника и рамки с током в магнитном поле.
- •Теорема Гаусса для магнитной индукции
- •28. Сила Лоренца, ее характеристики. Формула Лоренца. Движение заряженных частиц в магнитном и электрическом поле.
- •29.Эффект Холла, его объяснение.
- •Свойства
- •30.Магнетики. (Электронные микротоки в атоме). Прецессия электронов в атоме в магнитном поле. Магнитные свойства атомов и молекул.
- •Определение
- •Магнитный момент атома
- •31.Магнитное поле в веществе, сущность намагничивания. Вектор намагничивания. Магнитная восприимчивость и относительная магнитная проницаемость вещества.
- •32. Виды магнетиков(диамагнетики, парамагнетики, ферромагнетики) Зависимость их свойств от напряженности магнитного поля.
- •33.Ферромагнетики. Явление гистерезиса. Домены(в 10 вопросе). Точка Кюри.
- •34. Явление электромагнитной индукции. Закон Фарадея. Правила Ленца. Связь явления эми и закона сохранения энергии.
- •Физическая суть правила
- •35. Причины возникновения эдс индукции в неподвижном контуре, вращающимся контуре, движущимся проводнике.
- •36.Явление самоиндукции. Эдс самоиндукции. Индуктивность. Изменение тока в цепи при включении эдс.
- •38.Применение явления эми. Токи Фуко. Скин-эффект. Явление взаимной индукции. Трансформаторы.
- •39.Энергия магнитного поля. Плотность энергии магнитного поля.
- •40.Колебательный контур без активного сопротивления. Свободные электрические колебания. Параметры колебаний.
- •Характеристики
- •41.Затухающие электрические колебания. Логарифмический декремент затухания.
- •42.Вынужденые электрические колебания. Переменный ток.
- •43.Резонанс напряжений. Резонанс токов. Мощность в цепи переменного тока.
- •44.Электромагнитное поле. Теория Максвелла. Понятие о токе смещения.
- •[Править]Точная формулировка
- •45.Интегральные уравнения Максвелла.
- •46.Электромагнитные волны. Излучение эмв. Свойства эмв. Шкала эмв.
- •Шкала электромагнитных волн
3.Метод вычисления напряженности. Применение принципа суперпозиции для вычисления электрических полей неточечных зарядов. Напряжённость электрического поля точечного заряда
Для точечного заряда в электростатике верен закона Кулона
![]()
или
![]() .
.
![]() .
.
Исторически
закон Кулона был открыт первым, хотя с
теоретической точки зрения уравнения
Максвелла более фундаментальны. С этой
точки зрения он является их следствием.
Получить этот результат проще всего
исходя из теоремы
Гаусса,
учитывая сферическую симметрию задачи:
выбрать поверхность S в
виде сферы с центром в точечном заряде,
учесть, что направление ![]() будет
очевидно радиальным, а модуль этого
вектора одинаков везде на выбранной
сфере (так что E можно
вынести за знак интеграла), и тогда,
учитывая формулу для площади сферы
радиуса r:
будет
очевидно радиальным, а модуль этого
вектора одинаков везде на выбранной
сфере (так что E можно
вынести за знак интеграла), и тогда,
учитывая формулу для площади сферы
радиуса r: ![]() ,
имеем:
,
имеем:
![]()
откуда сразу получаем ответ для E.
Ответ для получается тогда интегрированием E:
![]()
Одной из основных задач электростатики является оценка параметров поля при заданном, стационарном, распределении зарядов в пространстве. Один из способов решения подобных задач основан на принципе суперпозиции. Суть его в следующем.
Если поле создается несколькими точечными зарядами, то на пробный заряд q действует со стороны заряда qk такая сила, как если бы других зарядов не было. Результирующая сила определится выражением:
|
|
|
|
– это принцип суперпозиции или независимости действия сил.
Т.к. ![]() ,
то
,
то ![]() –
результирующая напряженность поля в
точке, где расположен пробный заряд,
так же подчиняется
принципу суперпозиции:
–
результирующая напряженность поля в
точке, где расположен пробный заряд,
так же подчиняется
принципу суперпозиции:
|
|
|
(1.4.1) |
Это соотношение выражает принцип наложения или суперпозиции электрических полей и представляет важное свойство электрического поля. Напряженность результирующего поля, системы точечных зарядов равна векторной сумме напряженностей полей, созданных в данной точке каждым из них в отдельности.
Рассмотрим применение принципа суперпозиции в случае поля, созданного электрической системой из двух зарядов с расстоянием между зарядами, равными l (рис. 1.2).
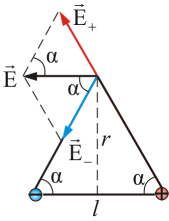 Рис.
1.2
Рис.
1.2
Поля,
создаваемые различными зарядами, не
влияют друг на друга, поэтому
вектор ![]() результирующего
поля нескольких зарядов
результирующего
поля нескольких зарядов ![]() может
быть найден по правилу сложения векторов
(правило параллелограмма)
может
быть найден по правилу сложения векторов
(правило параллелограмма)
|
|
|
|
![]() ,
, ![]() и
и ![]() ,
так как задача симметрична.
,
так как задача симметрична.
В данном случае
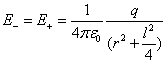 и
и
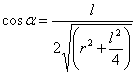
Следовательно,
|
|
4.Поток напряженности электрического поля. Теорема Остроградского-Гаусса. Примеры применения теоремы Гаусса для расчета электрических полей.
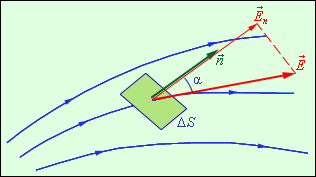
поток
Φ вектора напряженности электрического
поля. Понятие потока вектора ![]() аналогично
понятию потока вектора скорости
аналогично
понятию потока вектора скорости ![]() при
течении несжимаемой жидкости. Пусть в
пространстве, где создано электрическое
поле, расположена некоторая достаточно
малая площадка ΔS. Произведение модуля
вектора
на
площадь ΔS и на косинус угла α между
вектором
и
нормалью
при
течении несжимаемой жидкости. Пусть в
пространстве, где создано электрическое
поле, расположена некоторая достаточно
малая площадка ΔS. Произведение модуля
вектора
на
площадь ΔS и на косинус угла α между
вектором
и
нормалью ![]() к
площадке называется элементарным
потоком вектора напряженности через
площадку ΔS (рис. 4.3.1):
к
площадке называется элементарным
потоком вектора напряженности через
площадку ΔS (рис. 4.3.1):
ΔΦ = EΔS cos α = EnΔS, |
где ![]() –
модуль нормальной составляющей поля
–
модуль нормальной составляющей поля ![]()
|
Для
вывода теоремы Остроградского–Гаусса
необходимо ввести такие важные
вспомогательные понятия, как вектор
электрической индукции ![]() и
поток этого вектора Ф.
и
поток этого вектора Ф.
Известно,
что электростатическое поле часто
изображают при помощи силовых линий.
Предположим, что мы определяем
напряжённость в точке, лежащей на границе
раздела двух сред: воздуха(![]() =1)
и воды (
=81).
В этой точке при переходе из воздуха в
воду напряжённость электрического поля
согласно формуле
=1)
и воды (
=81).
В этой точке при переходе из воздуха в
воду напряжённость электрического поля
согласно формуле ![]() уменьшится
в 81 раз. Если пренебречь проводимостью
воды, то во столько же раз уменьшится
число силовых линий. При решении различных
задач на расчёт полей из-за прерывности
вектора напряжённости
уменьшится
в 81 раз. Если пренебречь проводимостью
воды, то во столько же раз уменьшится
число силовых линий. При решении различных
задач на расчёт полей из-за прерывности
вектора напряжённости ![]() на
границе раздела сред и на диэлектриках
создаются определённые неудобства.
Чтобы избежать их, вводится новый
вектор
,
который называется вектором электрической
индукции:
на
границе раздела сред и на диэлектриках
создаются определённые неудобства.
Чтобы избежать их, вводится новый
вектор
,
который называется вектором электрической
индукции: ![]()
Вектор
электрической индукции равен произведению
вектора
на
электрическую постоянную ![]() и
на диэлектрическую проницаемость среды
в данной точке
.
и
на диэлектрическую проницаемость среды
в данной точке
.
Очевидно,
что при переходе через границу двух
диэлектриков число линий электрической
индукции не изменяется для поля точечного
заряда ![]()
1. Напряженность электростатического поля, создаваемого равномерно заряженной сферической поверхностью.
Пусть
сферическая поверхность радиуса R (рис.
13.7) несет на себе равномерно распределенный
заряд q, т.е. поверхностная плотность ![]() заряда
в любой точке сферы будет одинакова.
заряда
в любой точке сферы будет одинакова.
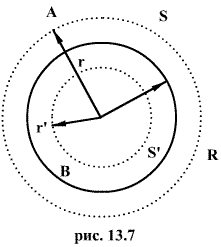
Заключим нашу сферическую поверхность в симметричную поверхность S с радиусом r>R. Поток вектора напряженности через поверхность S будет равен
![]()
По теореме Гаусса
![]()
Следовательно
-
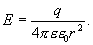
(13.8)
Для точек, находящихся на поверхности заряженной сферы радиуса R, по аналогии с вышеприведенным уравнением, можно написать
-

(13.9)
2. Электростатическое поле шара.
Пусть
имеем шар радиуса R, равномерно заряженный
с объемной плотностью . ![]()
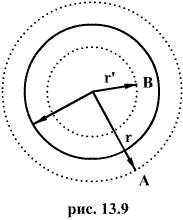
В
любой точке А, лежащей вне шара на
расстоянии r от его центра (r>R), его поле
аналогично полю точечного заряда ![]() ,
расположенного в центре шара. Тогда вне
шара
,
расположенного в центре шара. Тогда вне
шара
|
(13.10) |
а на его поверхности (r=R)
|
(13.11) |
В
точке В, лежащей внутри шара на расстояний
r от его центра (r>R), поле определяется
лишь зарядом ![]() ,
заключенным внутри сферы радиусом r.
Поток вектора напряженности через эту
сферу равен
,
заключенным внутри сферы радиусом r.
Поток вектора напряженности через эту
сферу равен
![]()
с другой стороны, в соответствии с теоремой Гаусса
![]()
Из сопоставления последних выражений следует
|
(13.12) |
где![]() -
диэлектрическая проницаемость внутри
шара.
-
диэлектрическая проницаемость внутри
шара.
3. Напряженность поля равномерно заряженной бесконечной прямолинейной нити (или цилиндра).
Предположим,
что полая цилиндрическая поверхность
радиуса R заряжена с постоянной линейной
плотностью ![]() .
.
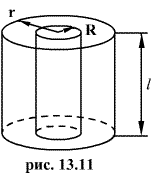
Проведем
коаксиальную цилиндрическую поверхность
радиуса ![]() Поток
вектора напряженности через эту
поверхность
Поток
вектора напряженности через эту
поверхность
![]()
По теореме Гаусса
![]()
Из последних двух выражений определяем напряженность поля, создаваемого равномерно заряженной нитью:
|
(13.13) |
4. Напряженность поля, создаваемого, бесконечной равномерно заряженной плоскостью.
|
(13.14) |
5. Работа сил электростатического поля по перемещению точечного заряда. Потенциальность электрического поля. Циркуляция напряженности. Выражение работы через разность потенциалов и потенциала через работу.
Работа перемещения заряда. На положительный точечный заряд q в электрическом поле с напряжённостью E действует сила F = q E. При перемещении заряда на отрезке dl силами поля совершается работа
dA = F dl = q E dl cos (E, dl).
При перемещении заряда q силами электрического поля на произвольном конечном отрезке из точки 1 в точку 2 эта работа равна
![]()
Потенциал электростатического поля — скалярная величина, равная отношению потенциальной энергии заряда в поле к этому заряду: φ = W / q = const - энергетическая характеристика поля в данной точке. Потенциал не зависит от величины заряда, помещенного в это поле. Потенциалом электростатического поля называют саклярную физическую величину, равную отношению потенциальной энергии заряда в поле к модулю этого заряда: φ = Wп / q = const Потенциал однородного поля: φ = Wп / q = -Exx + C Значение потенциала в данной точке зависит от выбора нулевого уровня для отсчёта потенциала. Этот уровень выбирают произвольно.
Разность потенциалов (напряжение) между двумя точками равна отношению работы поля при перемещении заряда из начальной точки в конечную к модулю этого заряда: U = φ1 - φ2 = -Δφ = A / q, A = -(Wп2 - Wп1) = -q(φ2 - φ1) = -qΔφ
Разность потенциалов измеряется в вольтах (В = Дж / Кл) Связь между напряжённостью электростатического поля и разностью потенциалов: Ex = Δφ / Δx Напряжённость электростатического поля направлена в сторону убывания потенциала. Измеряется в вольтах, делённых на метры (В / м).

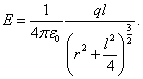
 1
1