8. Линейно зависимые и линейно независимые системы векторов. Свойства. Порождающие системы векторов. Примеры. Линейно зависимые и линейно независимые системы векторов

Пусть X — линейное пространство.

Определение. Система векторов x₁, x₂, … , x_n  X называется линейно зависимой, если существуют числа α₁, α₂, … , α_n  R , не все равные нулю (т.е. α₁² + α₂² + … + α_n² ≠ 0 ), такие, что

α₁x₁ + α₂x₂ + … + α_nx_n = θ.

Если это равенство выполняется только при α₁ = α₂ = … = α_n = 0 , то система векторов называется линейно независимой.

Вместо "линейно зависимая (или независимая) система векторов" можно говорить просто "линейно зависимые (или независимые) векторы".

Теорема Чтобы векторы x₁, x₂, … , x_n  X были линейно зависимы, необходимо и достаточно, чтобы хотя бы один из них являлся линейной комбинацией остальных.

Следствие. Два вектора x₁ и x₂ линейно зависимы тогда и только тогда, когда x₁ = αx₂ или x₂ = βx₁ при некоторых α, β  R , т.е. когда векторы x₁ и x₂ коллинеарны.

Свойства

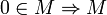• линейно зависимо

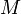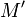• линейно независимо линейно независимо для всех

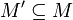
• линейно зависимо линейно зависимо для всех

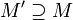
9. Базис. Теорема о базисе. Количество векторов в базисе. Размерность и ранг. Примеры. Координаты вектора в базисе.

Ба́зис (др.-греч. βασις, основа) — множество таких векторов в векторном пространстве, что любой вектор этого пространства может быть единственным образом представлен в виде линейной комбинации векторов из этого множества — базисных векторов.

Теоре́ма Ги́льберта о ба́зисе — одна из основных теорем о нётеровых кольцах:

Если R — нётерово кольцо, то кольцо многочленов R[x] также нётерово.

Пусть F — идеал в R[x] (мы здесь будем считать R коммутативным, для некоммутативных колец всё доказательство сохраняется, необходимо только считать все идеалы левыми), а p множество старших коэффициентов многочленов, его составляющих. Докажем, что p — идеал.

В самом деле, если a и b — элементы p, то a и b являются старшими коэффициентами некоторых многочленов из F — f(x)=axⁿ+… и g(x)=bx^m+… Если, например, m≥n, то a+b является старшим коэффициентом многочлена x^m-nf(x)+g(x)  F. Если a является старшим коэффициентом f(x) то ar является старшим коэффициентом rf(x)  F для любого элемента кольца r. Таким образом p — идеал, а так как R — нётерово кольцо, то p конечно порождается некоторыми элементами a₁, a₂…a_n, являющимися соответственно старшими коэффициентами многочленов f₁, f₂…f_n  F. Пусть наибольшая степень этих многочленов равна r. Можно считать что степень каждого из этих многочленов равна r (если она равна m<r, то можно сделать её такой домножая на x^r-m .

Аналогично доказывается что p_k — множество старших коэффициентов многочленов из F, степень которых k≤r (к этому множеству добавен 0 кольца) является идеалом, и потому идеалом, конечно порожденным элементами a_k1, a_k2…. Пусть они являются старшими коэффициентами многочленов f_k1,f_k2…  F степени k

Докажем, что эти многочлены f₁, …f_i…,f₁₁, …f_1i…,f_r-1,1, …f_r-1,i…  F порождают идеал F. Пусть f(x)=ax^s+… — какой-нибудь многочлен идеала F, по определению a  p. Если его степень s≥r то так как a по доказанному является линейной комбинацией a=r₁a₁+r₂a₂+ …r_na_n старших членов многочленов f₁, f₂…f_n  F степени r , то мы получим, что f(x)-r₁x^s-rf₁-r₂x^s-rf₂- …r_nx^s-rf_n будет многочленом степени, меньшей, чем s и также принадлежащим идеалу F. Повторяя при необходимости эту операцию несколько раз можно прийти к многочлену степени ≤r.

Для многочлена степени k<r применяется та же процедура, но с использованием многочленов f_k1,f_k2…  F, старшие коэффициенты которых порождают идеал p_k. Далее процедура повторяется, пока мы не придем к нулевому многочлену.

Рангом системы строк (столбцов) матрицы с строк и столбцов называется максимальное число линейно независимых строк (столбцов). Несколько строк (столбцов) называются линейно независимыми, если ни одна из них не выражается линейно через другие. Ранг системы строк всегда равен рангу системы столбцов, и это число называется рангом матрицы.

Ранг матрицы — наивысший из порядков миноров этой матрицы, отличных от нуля.

Ранг матрицы — Размерность образа линейного оператора, которому соответствует матрица.

Обычно ранг матрицы обозначается ( ) или . Оба обозначения пришли к нам из иностранных языков, потому и употребляться могут оба.

Пусть — прямоугольная матрица.

Тогда по определению рангом матрицы является:

• ноль, если — нулевая матрица;

• число 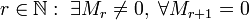, где 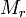— минор матрицы порядка , а — окаймляющий к нему минор порядка 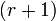, если они существуют.

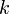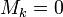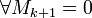Теорема (о корректности определения рангов). Пусть все миноры матрицы порядка равны нулю ( ). Тогда , если они существуют.

Векторы , составляющие базис в пространстве, называются базисными.

• Коэффициент линейной комбинации в линейном мире – модуль вектора.

• Пусть компланарен плоскости, в которой выбран базис

- разложение вектора по базису

• В пространстве:

- разложение вектора по базису в пространстве

- координаты в базисе, образованном векторами

Теорема (о единственном разложении вектора по базису): разложение вектора по базису единственно.

Теорема: при сложении векторов координаты складываются, а при умножении на скаляр – умножаются на этот скаляр.

Необходимое и достаточное условие коллинеарности двух векторов в координатной плоскости:

2 вектора || в т. и т.т. случае, если их координаты пропорциональны.