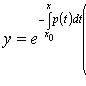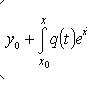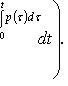5. Произведение комплексных чисел в тригонометрической форме. Возведение числа в степень и извлечение корня.

Теорема. (Об умножении комплексных чисел в тригонометрической форме записи.)

Пусть , где и , где – два произвольных комплексных числа записанных в тригонометрической форме. Тогда

. (13)

Доказательство.

, ч.т.д.

Теорема доказана.

Отсюда вытекает правило умножения комплексных чисел в тригонометрической форме записи.

Для того, чтобы перемножить два комплексных числа в тригонометрической форме записи нужно перемножить их модули, а аргументы сложить.

Следствие 1. Пусть k натуральное число и . Пусть далее , где – произвольные n комплексных чисел записанных в тригонометрической форме записи. Тогда

.

Доказательство проводится индукцией по числу сомножителей и предоставляется читателю.

Следствие 2. Пусть n натуральное число и – произвольное комплексное число в тригонометрической форме записи. Тогда

.

Доказательство сразу же следует из Следствия 1.

Теорема. (Свойства модуля комплексного числа.)

Пусть – произвольные комплексные числа и соответствующие точки на комплексной плоскости. Тогда:

1) и . Т.е. модуль произведения комплексных чисел равен произведению их модулей и модули противоположных чисел равны;

2) расстояние между точками и комплексной плоскости равно модулю разности соответствующих комплексных чисел: ;

3) ;

4) ;

Доказательство. 1) По предыдущей теореме имеем:

, где и ,

т.е. .

Таким образом, равенства и есть тригонометрическая форма записи числа , следовательно, по теореме о равенстве комплексных чисел в тригонометрической форме записи, имеем , ч.т.д.

Далее, т.к. , то по только что доказанному свойству , ч.т.д.

Заметим, что последнее равенство можно получить и из других соображений.

Противоположные числа на комплексной плоскости изображаются точками симметричными относительно начала координат. Действительно, пусть . Тогда и точки , имеют противоположные декартовые координаты. Значит, в силу симметрии, расстояния от этих точек до начала координат равны, т.е. , ч.т.д. Заметим, также, что такой же результат можно получить с помощью формулы (12) вычисления модуля комплексного числа.

2). Пусть , . Тогда и по формуле (12) имеем:

. (14)

С другой стороны, рассмотрим числа и как точки на комплексной плоскости. Тогда точка имеет декартовые координаты , а и искомое расстояние между ними вычисляется по формуле (14), ч.т.д.

3) Рассмотрим на комплексной плоскости точки , и начало координат О. В общем случае эти три точки являются вершинами треугольника :

рис.6.

Воспользуемся известным свойством треугольника: длина стороны треугольника не превосходит суммы длин двух его других сторон.

Мы только что доказали, что длина стороны этого треугольника равна , а длины сторон и равны по определению модулям чисел и : , . Отсюда и получаем, что .

Заменим в последнем неравенстве число на противоположное число , тогда получаем:

, ч.т.д.

Заметим, что равенство в этих неравенствах достигается тогда и только тогда, когда треугольник вырождается в отрезок прямой, т.е. когда все три точки О, и лежат на одной прямой.

4) , откуда следует

. Поменяв местами и , получаем

, откуда и следует доказываемое неравенство.

Теорема доказана.

Теория комплексных чисел имеет много приложений в различных областях математики. Не могу удержаться от искушения привести хотя бы один такой пример, относящийся к области теории чисел.

Определение. Говорят, что натуральное число n представимо в виде суммы двух квадратов, если существуют такие целые числа х и у, что выполняется равенство:

.

Теорема. Если два числа представимы в виде суммы двух квадратов, то их произведение также представимо в виде суммы двух квадратов.

Доказательство. Пусть и , где .

Нам нужно доказать, что найдутся два целых числа а и b такие, что .

С этой целью рассмотрим два комплексных числа и .

Тогда и по формуле (12) имеем: .

С другой стороны, , . Так как , то или , то отсюда получаем равенство: , где , ч.т.д.

Теорема доказана.

Линейная алгебра

6. Системы линейных уравнений. Эквивалентные системы линейных уравнений. Элементарные преобразования, метод Гаусса. Однородные и неоднородные системы.

Определение. Система линейных уравнений — это объединение из n линейных уравнений, каждое из которых содержит k переменных. Записывается это так:

Многие, впервые сталкиваясь с высшей алгеброй, ошибочно полагают, что число уравнений обязательно должно совпадать с числом переменных. В школьной алгебре так обычно и бывает, однако для высшей алгебры это, вообще говоря, неверно.

Определение. Решение системы уравнений — это последовательность чисел (k₁, k₂, ..., k_n), которая является решением каждого уравнения системы, т.е. при подстановке в это уравнение вместо переменных x₁, x₂, ..., x_n дает верное числовое равенство.

Эквивалентные системы линейных уравнений

Системы линейных уравнений называются эквивалентными, если множество их решений совпадает, то есть любое решение одной системы одновременно является решением другой, и наоборот.

Систему, эквивалентную данной, можно получить, в частности, заменив одно из уравнений на это уравнение, умноженное на любое отличное от нуля число. Эквивалентную систему можно получить также, заменив одно из уравнений суммой этого уравнения с другим уравнением системы. В общем, замена уравнения системы на линейную комбинацию уравнений даёт систему, эквивалентную исходной.

Система линейных алгебраических уравнений

эквивалентна системе

,

где — невырожденная матрица.

В частности, если сама матрица — невырожденная, и для неё существует обратная матрица , то решение системы уравнений можно формально записать в виде

Ме́тод Га́усса — классический метод решения системы линейных алгебраических уравнений (СЛАУ). Это метод последовательного исключения переменных, когда с помощью элементарных преобразований система уравнений приводится к равносильной системе ступенчатого (или треугольного) вида, из которой последовательно, начиная с последних (по номеру) переменных, находятся все остальные переменные

Пусть исходная система выглядит следующим образом

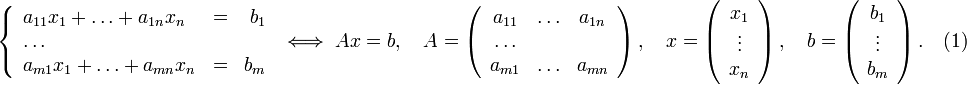
Матрица называется основной матрицей системы, — столбцом свободных членов.

Тогда согласно свойству элементарных преобразований над строками основную матрицу этой системы можно привести к ступенчатому виду(эти же преобразования нужно применять к столбцу свободных членов):

При этом будем считать, что базисный минор (ненулевой минор максимального порядка) основной матрицы находится в верхнем левом углу, то есть в него входят только коэффициенты при переменных ^[3].

Тогда переменные называются главными переменными. Все остальные называются свободными.

Если хотя бы одно число , где , то рассматриваемая система несовместна.

Пусть для любых .

Перенесём свободные переменные за знаки равенств и поделим каждое из уравнений системы на свой коэффициент при самом левом ( , где — номер строки):

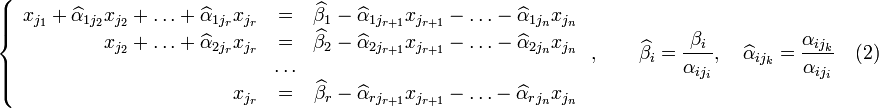где

Если свободным переменным системы (2) придавать все возможные значения и решать новую систему относительно главных неизвестных снизу вверх (то есть от нижнего уравнения к верхнему), то мы получим все решения этой СЛАУ. Так как эта система получена путём элементарных преобразований над исходной системой (1), то по теореме об эквивалентности при элементарных преобразованиях системы (1) и (2) эквивалентны, то есть множества их решений совпадают.

Линейное однородное уравнение первого порядка

Общее решение: .

Решение задачи Коши, y(x₀) = y₀:

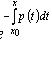
Линейное неоднородное уравнение первого порядка

Общее решение:

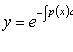
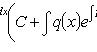
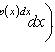
Решение задачи Коши, y(x₀) = y₀: