
- •Группы, кольца, поля. Определения и примеры. Кольца из 2-5 элементов. Область целостности.
- •Комплексные числа. Определение, нормальная форма. Поле комплексных чисел.
- •Комплексные числа на плоскости. Модуль и аргумент числа, тригонометрическая форма. Сопряженные числа и их свойства.
- •Произведение комплексных чисел в тригонометрической форме. Возведение числа в степень и извлечение корня.
- •7. Векторные пространства. Определение и примеры. Свойства нуля. Линейное выражение.
- •8. Линейно зависимые и линейно независимые системы векторов. Свойства. Порождающие системы векторов. Примеры. Линейно зависимые и линейно независимые системы векторов
- •9. Базис. Теорема о базисе. Количество векторов в базисе. Размерность и ранг. Примеры. Координаты вектора в базисе.
- •10. Матрицы. Определение матрицы. Сложение матриц, умножение матрицы на число и транспонирование матрицы. Их свойства.
- •11. Умножение матриц. Свойства, примеры.
- •Запись системы линейных уравнений в матричном виде. Связь между изменением базиса и матрицами. Двойное изменение базиса. Координаты вектора в новом базисе.
- •Изменение координат вектора при изменении базиса
- •Элементарные преобразования в матричном виде. Теорема о ранге матрицы.
- •Инвариантность ранга при элементарных преобразованиях
- •Эквивалентность слау при элементарных преобразованиях
- •Свойства ранга матрицы. Связь с обратными матрицами. Теорема Кронекера-Капелли.
- •Свойства
- •Необходимость
- •Достаточность
- •Следствия
- •15. Перестановки. Произведение перестановок. Транспозиция. Перестановка как произведение транспозиций и транспозиция как произведение транспозиций соседних элементов.
- •16. Инверсии в перестановке. Четность перестановки. Связь с транспозициями. Четность произведения перестановок.
- •17. Определение определителя. Определители небольших порядков. Начальные свойства (1-6).
- •18. Дальнейшие свойства. Алгебраическое дополнение и минор. Разложение по строке. Примеры.
- •19. Теорема Крамера. Нахождение обратной матрицы с помощью определителей. Определитель произведения.
- •§2 Свойства умножения матриц
- •20.Определение многочлена от одной переменной. Действия с многочленами и их свойства. Пространство и кольцо многочленов.
- •21. Нормальная форма записи многочленов. Степень многочлена и ее свойства. Кольцо многочленов над областью целостности.
- •22. Значение многочлена в точке. Деление с остатком. Две теоремы о делении с остатком. Схема Горнера.
- •Деление с остатком
- •Теорема Безу
- •23. Теорема Безу. Корень многочлена, количество корней у многочлена. Теорема о тождестве. Алгебраически замкнутые поля, основная теорема алгебры (б/д). Разложение на линейные сомножители.
- •24. Решение уравнений третьей степени.
- •25.Решение уравнений четвертой степени.
- •27. Взаимно простые многочлены. Определение, свойства
- •29. Неприводимые многочлены над полями комплексных и вещественных чисел.
- •31. Многочлены от нескольких переменных. Симметрические многочлены. Теорема о симметрических многочленах.
7. Векторные пространства. Определение и примеры. Свойства нуля. Линейное выражение.
Ве́кторное (лине́йное) простра́нство — основной объект изучения линейной алгебры.
Определение
Линейное, или векторное пространство
![]() над
полем
над
полем
![]() —
это непустое
множество
—
это непустое
множество
![]() ,
на котором введены операции
,
на котором введены операции
сложения, то есть каждой паре элементов множества
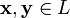 ставится
в соответствие элемент того же множества,
обозначаемый
ставится
в соответствие элемент того же множества,
обозначаемый
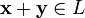 и
иумножения на скаляр (то есть элемент поля ), то есть любому элементу
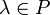 и
любому элементу
и
любому элементу
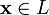 ставится
в соответствие единственный элемент
из
,
обозначаемый
ставится
в соответствие единственный элемент
из
,
обозначаемый
 .
.
При этом на операции накладываются следующие условия:
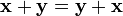 ,
для любых
(коммутативность
сложения);
,
для любых
(коммутативность
сложения);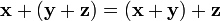 ,
для любых
,
для любых
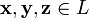 (ассоциативность
сложения);
(ассоциативность
сложения);существует такой элемент
 ,
что
,
что
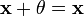 для
любого
(существование
нейтрального элемента относительно
сложения), в частности
не
пусто;
для
любого
(существование
нейтрального элемента относительно
сложения), в частности
не
пусто;для любого существует такой элемент
 ,
что
,
что
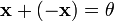 (существование
противоположного элемента относительно
сложения).
(существование
противоположного элемента относительно
сложения).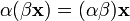 (ассоциативность
умножения на скаляр);
(ассоциативность
умножения на скаляр);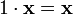 (унитарность:
умножение на нейтральный (по умножению)
элемент поля P сохраняет вектор).
(унитарность:
умножение на нейтральный (по умножению)
элемент поля P сохраняет вектор).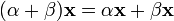 (дистрибутивность
умножения на вектор относительно
сложения скаляров);
(дистрибутивность
умножения на вектор относительно
сложения скаляров);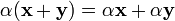 (дистрибутивность
умножения на скаляр относительно
сложения векторов).
(дистрибутивность
умножения на скаляр относительно
сложения векторов).
Элементы множества называют векторами, а элементы поля — скалярами. Свойства 1-4 совпадают с аксиомами абелевой группы.
Простейшие свойства
Векторное пространство является абелевой группой по сложению.
Нейтральный элемент является единственным, что вытекает из групповых свойств.
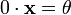 для
любого
.
для
любого
.Для любого противоположный элемент является единственным, что вытекает из групповых свойств.
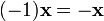 для
любого
.
для
любого
.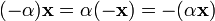 для
любых
для
любых
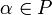 и
.
и
. для
любого
.
для
любого
.
Векторное пространство, математическое понятие, обобщающее понятие совокупности всех (свободных) векторов обычного трёхмерного пространства.
Определение В. п. Для векторов трёхмерного пространства указаны правила сложения векторов и умножения их на действительные числа (см. Векторное исчисление). В применении к любым векторам х, у, z и любым числам a, b эти правила удовлетворяют следующим условиям (условия А):
Векторным (или линейным) пространством называется множество R, состоящее из элементов любой природы (называемых векторами), в котором определены операции сложения элементов и умножения элементов на действительные числа, удовлетворяющие условиям А (условия 1—3 выражают, что операция сложения, определённая в В. п., превращает его в коммутативную группу).
Выражение
a1e1 + a2e2 + … + anen (1)
называется линейной комбинацией векторов e1, e2,..., en с коэффициентами a1, a2,..., an. Линейная комбинация (1) называется нетривиальной, если хотя бы один из коэффициентов a1, a2,..., an отличен от нуля. Векторы e1, e2,..., en называются линейно зависимыми, если существует нетривиальная комбинация (1), представляющая собой нулевой вектор. В противном случае (то есть если только тривиальная комбинация векторов e1, e2,..., en равна нулевому вектору) векторы e1, e2,..., en называется линейно независимыми.
Векторы (свободные) трёхмерного пространства удовлетворяют следующему условию (условие В): существуют три линейно независимых вектора; любые четыре вектора линейно зависимы (любые три ненулевых вектора, не лежащие в одной плоскости, являются линейно независимыми).
В. п. называется n-мepным (или имеет "размерность n"), если в нём существуют n линейно независимых элементов e1, e2,..., en, а любые n + 1 элементов линейно зависимы (обобщённое условие В). В. п. называются бесконечномерным, если в нём для любого натурального n существует n линейно независимых векторов. Любые n линейно независимых векторов n-мepного В. п. образуют базис этого пространства. Если e1, e2,..., en — базис В. п., то любой вектор х этого пространства может быть представлен единственным образом в виде линейной комбинации базисных векторов:
x = a1e1 + a2e2 +... + anen.
При этом числа a1, a2,..., an называются координатами вектора х в данном базисе.
Примеры В. п. Множество всех векторов трёхмерного пространства образует, очевидно, В. п. Более сложным примером может служить так называемое n-мерное арифметическое пространство. Векторами этого пространства являются упорядоченные системы из n действительных чисел: l 1, l 2,..., l n. Сумма двух векторов и произведение на число определяются соотношениями:
(l1, l2, …, ln) + (m1, m2, …, mn) = (l1 + m1, l2 + m2, …, ln + mn);
a(l1, l2, …, ln) = (al1, al2, …, aln).
Базисом в этом пространстве может служить, например, следующая система из n векторов e1 = (1, 0,..., 0), e2 = (0, 1,..., 0),..., en = (0, 0,..., 1).
Множество R всех многочленов a0 + a1u + … + anun (любых степеней n) от одного переменного с действительными коэффициентами a0, a1,..., an с обычными алгебраическими правилами сложения многочленов и умножения многочленов на действительные числа образует В. п. Многочлены 1, u, u2,..., un (при любом n) линейно независимы в R, поэтому R — бесконечномерное В. п.
