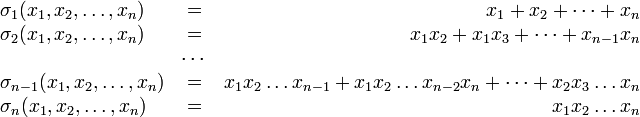Теорема Кронекера — Капелли: Система линейных алгебраических уравнений совместна тогда и только тогда, когда ранг её основной матрицы равен рангу её расширенной матрицы. В частности:

1. Количество главных переменных системы равно рангу системы.

2. Совместная система будет определена (её решение единственно), если ранг системы равен числу всех её переменных.

Теоре́ма Кро́некера — Капе́лли — критерий совместности системы линейных алгебраических уравнений: Система линейных алгебраических уравнений совместна тогда, когда ранг её основной матрицы равен рангу её расширенной матрицы, причём система имеет единственное решение, если ранг равен числу неизвестных, и бесконечное множество решений, если ранг меньше числа неизвестных.

Доказательство (условия совместности системы)

Необходимость

Пусть система совместна. Тогда существуют числа такие, что . Следовательно, столбец является линейной комбинацией столбцов матрицы . Из того, что ранг матрицы не изменится, если из системы его строк (столбцов) вычеркнуть или приписать строку (столбец), которая является линейной комбинацией других строк (столбцов) следует, что .

Достаточность

Пусть . Возьмем в матрице какой-нибудь базисный минор. Так как , то он же и будет базисным минором и матрицы . Тогда согласно теореме о базисном миноре последний столбец матрицы будет линейной комбинацией базисных столбцов, то есть столбцов матрицы . Следовательно, столбец свободных членов системы является линейной комбинацией столбцов матрицы .

Следствия

• Количество главных переменных системы равно рангу системы.

• Совместная система будет определена (её решение единственно), если ранг системы равен числу всех её переменных.

15. Перестановки. Произведение перестановок. Транспозиция. Перестановка как произведение транспозиций и транспозиция как произведение транспозиций соседних элементов.

В комбинаторике перестано́вка — это упорядоченный набор чисел обычно трактуемый как биекция на множестве , которая числу i ставит соответствие i-й элемент из набора. Число n при этом называется порядком перестановки.

В теории групп под перестановкой (подстановкой) произвольного множества подразумевается биекция этого множества на себя.

• Число всех перестановок порядка равно числу размещений из n по n, то есть факториалу:^[1][2][3][4]

• Композиция определяет операцию произведения на перестановках одного порядка: 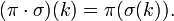Относительно этой операции множество перестановок порядка n образует группу, которую называют симметрической и обычно обозначают .

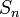• Любая группа является подгруппой группы перестановок множества элементов этой группы (теорема Кэли). При этом каждый элемент 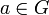сопоставляется с перестановкой 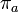, задаваемой тождеством 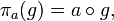где g — произвольный элемент группы G, а — групповая операция.

Подстановки и произведения циклов

Перестановка множества может быть записана в виде подстановки, например:

где и

Перестановку также можно записать в виде произведения непересекающихся циклов, причём единственным образом с точностью до порядка следования циклов в произведении. Например:

Теперь разобьем все п\ перестановок п элементов на два класса, по признаку, кажущемуся довольно искусственным, но именно это разбиение будет нужно для разумного правила расстановки знаков в определителе. Пусть (а,, о&2, •••, OLn)—некоторая перестановка чисел 1, 2, ... п. Скажем, что пара элементов (а,-, а;), і <С/, образует инверсию, если сх< > а/. Число всех пар элементов перестановки, образующих инверсию, называется числом инверсий в перестановке и обозначается inv(cxi, а?, ап). Так, inv(3, 5, 1, 4, 2, 6, 8, 7) = 7 (инверсии образуют пары (З, 1), (3, 2), (5, 1), (5, 4), Перестановки, содержащие четное число инверсий, называются четными, содержащие нечетное число инверсий — нечетными. Подстановкой на множестве {1, 2, п} называется взаимно однозначное отображение множества на себя. Удобно задавать подстановку прямым указанием замен для каждого элемента, посредством записи образа под прообразом. Так, запись 1, 2, 3, 4, 5, соответственно, на 5, 1, 3, 2, 4; порядок расположения ее столбцов безразличен. В такой записи в «числителе» и в «знаменателе» оказываются перестановки. Удобно в «числителе» записывать элементы в натуральном расположении. Последовательное применение двух подстановок приводит к подстановке, называемой их произведением. Так, / 1 2 3 4 5 6 \ / 1 2 3 4 5 6 \ _ / 1 2 3 4 5 6\ \5 2 1 6 4 3j"U 1 2 4 3 5 J-VS 1 6 5 4 2) (мы считаем первой действующей ту подстановку, которая записана слева). Почти очевидно, что при умножении подстановок имеет место ассоциативность. Действительно, пусть а, х и ср — подстановки на-множестве {1, 2, п}. Сделать (от)ср— все равно, что сначала сделать а, потом т, затем ср; сделать же о (тер) — все равно, что сначала сделать о, потом тер, т. е. к результату применения о применить т и затем ср. Тождественная подстановка, при которой каждому элементу сопоставляется он сам, играет роль единицы в этом умножении. Если запись подстановки а перевернуть, т. е. ее числитель сделать знаменателем, а знаменатель числителем, мы придем к обратной подстановке а~1, произведение которой на а как в одном, так и в обратном порядке, дает единичную подстановку. Умножение подстановок, вообще говоря, некоммутативно, например, V2 1 ЗМ2 3 \) \Ъ 2 і)' \2 З l)\2 1 .з)~\ 1 3 2)- Число всех возможных подстановок на множестве из п элементов равно п\, ибо таково число возможных знаменателей при фиксированном числителе. (5, 2), (4, 2), (8, 7)). 2 3 4 1 3 2 задает подстановку, которая заменяет элементы

16. Инверсии в перестановке. Четность перестановки. Связь с транспозициями. Четность произведения перестановок.

Каждая последовательность k различных элементов с учетом порядка называется перестановкой этих элементов. Следовательно, перестановки из k элементов отличаются друг от друга только порядком входящих в них элементов. Например из первых шести чисел натурального ряда можно образовать следующие перестановки : 1,2,3,4,5,6 4,6,5,1,3,2 2,1,6,5,4,3 . . . и другие. По определению, инверсию образуют два числа в перестановке когда меньшее из них расположено правее большего. Каждой перестановке можно сопоставить число инверсий в ней, которое подсчитывается следующим образом: для каждого из чисел определяют количество стоящих правее его меньших чисел, и полученные результаты складываются.

Перестановка называется четной, если число инверсий в ней четно, и нечетной - в противном случае. В частности, рассмотренная выше перестановка нечетная, так как количество инверсий в ней равно семь.

Теорема. Любая транспозиция соседних элементов перестановки меняет четность перестановки на противоположную.

Доказательство. Пусть дана перестановка , в которой мы выполним транспозицию (i j) и получим перестановку . Сразу заметим, что все пары, которые образовывали инверсию в старой перестановке, образуют инверсию и в новой, кроме возможно одной пары: (i, j). Если эта пара давала инверсию в старой перестановке, то в новой уже нет и число инверсий уменьшается на 1. Если же эта пара не образовывала инверсию в старой перестановке, то в новой образует инверсию и число инверсий увеличивается на 1. В любом случае, число инверсий изменяется на 1, а следовательно, меняется четность перестановки.

Теорема доказана.

Теорема. Любая транспозиция любых двух элементов перестановки меняет четность перестановки на противоположную.

Доказательство. Пусть выполняется транспозицию (i j) и пусть между элементами i и j находится m других элементов. Легко видеть, что такую транспозицию можно выполнить за транспозицию соседних элементов, откуда и следует теорема.

Теорема доказана.

Транспозицией называется перестановка, в которой все элементы

кроме двух остаются на месте, а два меняются местами

Лемма. Перестановка, обратная к транспозиции – транспозиция.

Лемма. Всякую перестановку можно представить в виде произведения

нескольких транспозиций. Обратную – произведения обратных

транспозиций в обратном порядке.

Инверсией перестановки называется нарушение порядка в

нижней строке перестановки. Четность перестановки положительна

(четная перестановка), если число инверсий – четное, и отрицательна

– в противном случае.

Лемма. Транспозиция – нечетная перестановка.

Лемма. Четность перестановки совпадает с четностью числа

транспозиций. Док. Индукция по числу перестановок. Следствие.

Четность произведения перестановок = произведению их четностей.

Четность подстановки

Определение 6. Пусть — разложение подстановки в произведение транспозиций. Тогда число называется знаком⁷⁾(четностью) подстановки . Подстановка называется четной⁸⁾, если и нечетной⁹⁾ в противном случае.

Предложение 3. Четность подстановки не зависит от способа разложения подстановки в произведение транспозиций.

Предложение 4. Для двух подстановок и четность их произведения равна произведению четностей:

Доказательство.

Пусть , , значит, и . Тогда — разложение подстановки в произведение транспозиций. Поэтому

.

Предложение 5. Пусть — цикл длины . Тогда его четность равна .

Доказательство.

Утверждение следует из того, что цикл длины представим в виде произведения -й транспозиции

Утверждение следует из того, что цикл длины представим в виде произведения -й транспозиции

.

Определение 7. Пусть — разложение подстановки в произведение независимых циклов длин . Число называется декрементом¹⁰⁾ подстановки .

Предложение 6. Пусть — разложение подстановки в произведение независимых циклов длин . Тогда четность подстановки вычисляется по формуле

.

По предложению 5 для . По предложению 4

.

Пример 6. Любая транспозиция — это нечетная подстановка. Подстановка из примера 4 нечетная, так как декремент — нечетное число.

Пример 7. Любая подстановка, в разложении которой на независимые циклы все циклы имеют нечетные длины , четна, так как ее декремент — это сумма четных чисел .

17. Определение определителя. Определители небольших порядков. Начальные свойства (1-6).

Определи́тель (или детермина́нт) — одно из основных понятий линейной алгебры. Определитель матрицы является многочленом от элементов квадратной матрицы (то есть такой, у которой количество строк и столбцов равно). В общем случае матрица может быть определена над любым коммутативным кольцом, в этом случае определитель будет элементом того же кольца.

Определитель матрицы А обозначается как: det(A), |А| или Δ(A).

Определение через разложение по первой строке

Для матрицы первого порядка детерминантом является сам единственный элемент этой матрицы:

Для матрицы детерминант определяется как

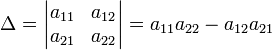
Для матрицы определитель задаётся рекурсивно:

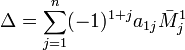, где — дополнительный минор к элементу . Эта формула называется разложением по строке.

В частности, формула вычисления определителя матрицы такова:

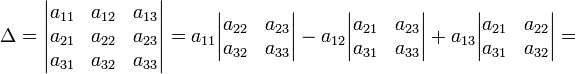
Легко доказать, что при транспонировании определитель матрицы не изменяется (иными словами, аналогичное разложение по первому столбцу также справедливо, то есть даёт такой же результат, как и разложение по первой строке):

Доказательство

Также справедливо и аналогичное разложение по любой строке (столбцу):

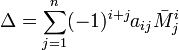
Обобщением вышеуказанных формул является разложение детерминанта по Лапласу (Теорема Лапласа), дающее возможность вычислять определитель по любым k строкам (столбцам):

Определитель первого порядка равен тому единственному элементу, из которого состоит соответствующая матрица.

Определитель второго порядка вычислим, например, по элементам первой строки

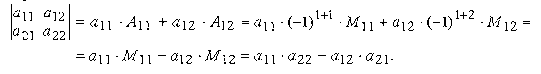
Запишем разложение данного определителя по элементам второй строки

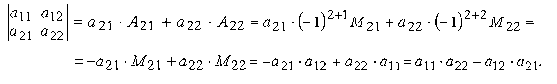
Полученный результат совпадает с результатом вычисления определителя по первой строке. Этот же результат получится и при разложении по любому из столбцов. Рекомендуем это проверить самостоятельно.

Из сказанного можно заключить, что определитель второго порядка равен произведению элементов, стоящих на главной диагонали, минус произведение элементов, стоящих на побочной диагонали.

Пример. .

Найдем определитель третьего порядка, раскладывая его по элементам, например, третьего столбца

.Свойства определителей Теорема 1. При транспонировании величина определителя не меняется. Следствие. Строки и столбцы в определителе равноправны, т.е. свойства, справедливые для строк, будут справедливы и для столбцов. Теорема 2. Если все элементы одной строки определителя умножить на одно и то же число, то и весь определитель умножится на это число. Следствие. Постоянный множитель строки можно выносить за знак определителя. Теорема 3. Если в определителе поменять местами две строки, то определитель сменит знак на противоположный. Следствие 1. Определитель, у которого две строки равны, равен нулю. Следствие 2. Если в определителе две строки пропорциональны, то такой определитель равен нулю. Теорема 4. Если строка определителя представлена в виде алгебраической суммы нескольких слагаемых, то определитель равен алгебраической сумме определителей, у которых в первом определителе в данной строке стоит первое слагаемое, во втором - второе слагаемое и т.д. Следствие. Если строки определителя линейно зависимы, то такой определитель равен нулю. Теорема 5. Если к элементам одной строки определителя прибавить соответствующие элементы другой, умноженные на одно и то же число, то определитель не изменится.

18. Дальнейшие свойства. Алгебраическое дополнение и минор. Разложение по строке. Примеры.

Основные свойства определителей.

Сформулируем и докажем основные свойства определителей 2-го и 3-го порядка (доказательство проведем для определителей 3-го порядка).

Свойство 1. Определитель не изменяется при транспонировании, т.е.

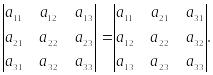
Доказательство.

=

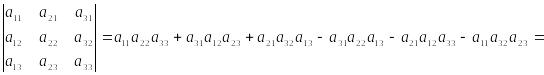
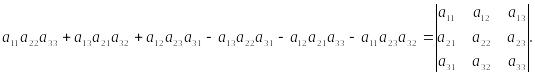
Замечание. Следующие свойства определителей будут формулироваться только для строк. При этом из свойства 1 следует, что теми же свойствами будут обладать и столбцы.

Свойство 2. При умножении элементов строки определителя на некоторое число весь определитель умножается на это число, т.е.

.

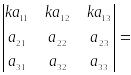
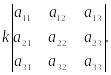Доказательство.

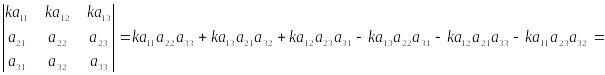
Свойство 3. Определитель, имеющий нулевую строку, равен 0.

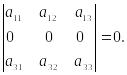
Доказательство этого свойства следует из свойства 2 при k = 0.

Свойство 4. Определитель, имеющий две равные строки, равен 0.

Доказательство.

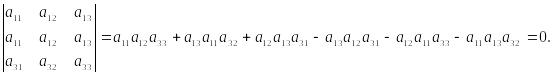
Свойство 5. Определитель, две строки которого пропорциональны, равен 0.

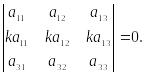
Доказательство следует из свойств 2 и 4.

Свойство 6. При перестановке двух строк определителя он умножается на –1.

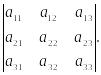
Доказательство.

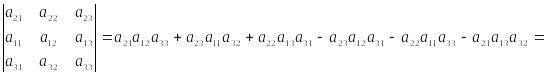
Свойство 7.

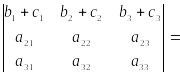
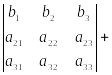
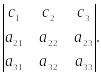
Доказательство этого свойства можно провести самостоятельно, сравнив значения левой и правой частей равенства, найденные с помощью определения 1.5.

Свойство 8. Величина определителя не изменится, если к элементам одной строки прибавить соответствующие элементы другой строки, умноженные на одно и то же число.

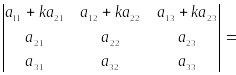
Доказательство следует из свойств 7 и 5.

Свойство 9. Если к элементам i-го ряда прибавить линейную комбинацию соответствующих элементов нескольких параллельных рядов, то значение определителя не изменится:

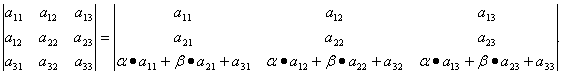
Справедливость этого равенства вытекает из свойства 8.

Миноры и алгебраические дополнения.

Определение. Если в определителе n-го порядка выбрать произвольно pстрок и p столбцов (p < n), то элементы, находящиеся на пересечении этих строк и столбцов, образуют матрицу порядка .

Определитель этой матрицы называется минором исходного определителя. Например, рассмотрим определитель :

Из строк и столбцов с чётными номерами построим матрицу:

Определитель

называется минором определителя . Получили минор второго порядка. Ясно, что из можно построить различные миноры первого, второго и третьего порядка.

Если взять элемент и вычеркнуть в определителе строку и столбец, на пересечении которых он стоит, то получим минор, называемый минором элемента ,который обозначим через :

.

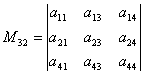Если минор умножить на , где 3 + 2 – сумма номеров строки и столбца, на пересечении которых стоит элемент то полученное произведение называется алгебраическим дополнением элемента и обозначается ,

т.е.

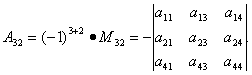
Вообще, минор элемента будем обозначать ,а алгебраическое дополнение ,

причём

(4)

Для примера вычислим алгебраические дополнения элементов и определителя третьего порядка :

По формуле (4) получим

Для вычисления определителя n-го порядка полезно знать следующую теорему: определитель равен сумме произведений элементов какой-либо строки на их алгебраические дополнения, т.е.

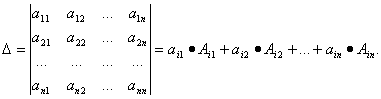(i = 1, 2, ..., n)

Пример 3

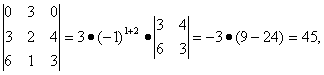
здесь разложение проведено по элементам первой строки.

Пример 4.

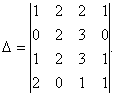
Предварительно вычтем из первой и третьей строк элементы четвёртой строки, тогда будем иметь

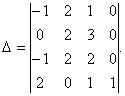
В четвёртом столбце полученного определителя три элемента – нули. Поэтому выгоднее разложить этот определитель по элементам четвёртого столбца, так как три первых произведения будут нулями. Поэтому

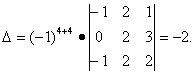
.Метод разложения определителя по строке(столбцу). Для реализации данного метода необходимо проделать следующее.

• Выбрать строку или столбец данного определителя. Выберем например 1 строку.

• Взять первый элемент этой строки и записать его в правой части равенства. Это будет первый сомножитель первого слагаемого результата.

• Мысленно вычеркнуть первую строку и первый столбец данной матрицы, поскольку на пересечений первой строки и первого столбца стоит выбранный элемент матрицы. В результате получится матрица на порядок меньшая исходной. Ее определитель нужно записать в результат вычисления в качестве второго сомножителя первого слагаемого разложения определителя.

• Число минус единица надо возвести в степень, которая определяется как сумма номера строки и номера столбца. Это будет третий сомножитель первого члена разложения определителя по первой строке.

• Второй и последующие члены разложения определяются аналогично.

Таким оразом данный метод сводит задачу вычисления определителя к задаче решения определителя более низкого порядка.

19. Теорема Крамера. Нахождение обратной матрицы с помощью определителей. Определитель произведения.

Данный метод также применим только в случае систем линейных уравнений, где число переменных совпадает с числом уравнений. Кроме того, необходимо ввести ограничения на коэффициенты системы. Необходимо, чтобы все уравнения были линейно независимы, т.е. ни одно уравнение не являлось бы линейной комбинацией остальных.

Для этого необходимо, чтобы определитель матрицы системы не равнялся 0.

det A  0;

Действительно, если какое- либо уравнение системы есть линейная комбинация остальных, то если к элементам какой- либо строки прибавить элементы другой, умноженные на какое- либо число, с помощью линейных преобразований можно получить нулевую строку. Определитель в этом случае будет равен нулю.

Теорема. (Правило Крамера):

Теорема. Система из n уравнений с n неизвестными

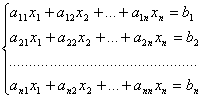
в случае, если определитель матрицы системы не равен нулю, имеет единственное решение и это решение находится по формулам:

x_i = _i/, где

 = det A, а _i – определитель матрицы, получаемой из матрицы системы заменой столбца i столбцом свободных членов b_i.

_i =

Пример.

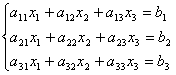
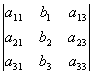A = ; ₁= ; ₂= ; ₃= ;

x₁ = ₁/detA; x₂ = ₂/detA; x₃ = ₃/detA;

Пример. Найти решение системы уравнений:

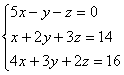
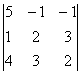 = = 5(4 – 9) + (2 – 12) – (3 – 8) = -25 – 10 + 5 = -30;

₁ = = (28 – 48) – (42 – 32) = -20 – 10 = -30.

x₁ = ₁/ = 1;

₂ = 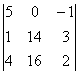= 5(28 – 48) – (16 – 56) = -100 + 40 = -60.

x₂ = ₂/ = 2;

₃ = 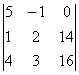= 5( 32 – 42) + (16 – 56) = -50 – 40 = -90.

x₃ = ₃/ = 3.

Конец формы

Матрица является обратной для матрицы , определитель которой отличен от нуля , если справедливы равенства , где E – единичная матрица порядка n на n. Как же находить обратную матрицу для данной? Во-первых, нам потребуются понятия транспонированной матрицы, минора матрицы и алгебраического дополнения элемента матрицы. Минор k-ого порядка матрицы A порядка m на n – это определитель матрицы порядка k на k, которая получается из элементов матрицы А, находящихся в выбранных k строках и k столбцах. (k не превосходит наименьшего из чисел m или n). Минор (n-1)-ого порядка, который составляется из элементов всех строк, кроме i-ой, и всех столбцов, кроме j-ого, квадратной матрицы А порядка n на n обозначим как . Иными словами, минор получается из квадратной матрицы А порядка n на n вычеркиванием элементов i-ой строки и j-ого столбца. Для примера запишем, минор 2-ого порядка, который получаетсся из матрицы 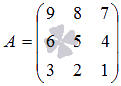выбором элементов ее второй, третьей строк и первого, третьего столбцов 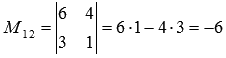. Также покажем минор, который получается из матрицы вычеркиванием второй строки и третьего столбца . Проиллюстрируем построение этих миноров: 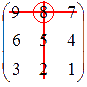и .

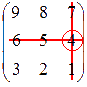Понятие обратной матрицы, равенство , свойства операций над матрицами и свойства определителя матрицы позволяют обосновать следующие свойства обратной матрицы:

1. Для невырожденной квадратной матрицы А справедливо равенство .

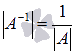2. Для обратимой матрицы А выполняется равенство .

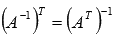3. Для любого отличного от нуля числа k справедливо равенство .

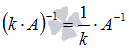4. Для невырожденных квадратных матриц А и В одного порядка выполняется равенство .

Составим алгоритм нахождения обратной матрицы с использованием равенства .

1. Вычисляем определитель матрицы А и убеждаемся, что он отличен от нуля (в противном случае матрица А необратима).

2. Строим 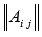- матрицу из алгебраических дополнений элементов .

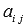3. Транспонируем матрицу , тем самым получаем .

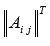4. Умножаем каждый элемент матрицы на число 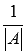. Этой операцией завершается нахождение обратной матрицы .

5. Проводим проверку результата, вычисляя произведения 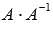и 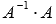. Если , то обратная матрица найдена верно, в противном случае где-то была допущена ошибка.

Умножение матриц

,

,

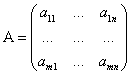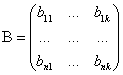
Опр. Произведением матрицы на матрицу называется матрица . , где

, где

Говорят, что есть скалярное произведение -строки матрицы на -столбец матрицы .

, где

Пример:

§2 Свойства умножения матриц

Умножение матриц ассоциативно:

1) , если определены произведения матриц и

Доказательство:

Пусть , так как определено , то и определено , то

Определим матрицы:

а)

б)

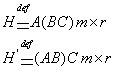(1) матрицы, тогда имеют одинаковую размерность

2) Покажем, что на одинаковых местах в матрицах расположены одинаковые элементы

из равенства(1) (2), (3).Подставляя (3) в (2) получим:

, тогда (4), (5).Подставляя (5) в (4) получим:

Вывод: Матрицы имеют одинаковую размерность и на одинаковых местах расположены одинаковые элементы.

Умножение матриц дистрибутивно :

Доказательство:

так как определено , то и определено , то

размерности

размерности

Матрицы имеют одинаковую размерность, покажем расположение одинаковых элементов:

,

,

Вывод: На одинаковых местах расположены одинаковые элементы.

3. , . Если определены матрицы, то доказательство проводим аналогично свойству 2.

4. , : , если определена матрица

Доказательство:

. Пусть ,

, ,

5. Умножение матриц в общем случае не коммутативно.Рассмотрим это на примере:

, тогда

Многочлены

20.Определение многочлена от одной переменной. Действия с многочленами и их свойства. Пространство и кольцо многочленов.

Многочлен (или полином) от n переменных — это конечная формальная сумма вида

,

где есть набор из целых неотрицательных чисел (называется мультииндекс), — число (называемое «коэффициент многочлена»), зависящее только от мультииндекса I.

В частности, многочлен от одной переменной есть конечная формальная сумма вида

где фиксированные коэффициенты, а — переменная.

С помощью многочлена выводятся понятия алгебраическое уравнение и алгебраическая функция.

Операции над многочленами

Многочлены можно складывать, вычитать и умножать по обычным правилам раскрытия скобок и приведения подобных членов. При этом в результате снова получается многочлен. Указанные операции обладают известными свойствами:

f (x) +g (x) =g (x) +f (x),

f (x) + (g (x) +h (x)) = (f (x) +g (x)) +h (x),

f (x) g (x) =g (x) f (x),

f (x) (g (x) h (x)) = (f (x) g (x)) h (x),

f (x) (g (x) +h (x)) =f (x) g (x) +f (x) h (x).

Установим еще несколько полезных свойств операций над многочленами.

Пусть даны два многочлена f (x) =a_nxⁿ+a_n-1x^n-1+... +a₁x+a₀, a_n≠0, и g (x) =b_mx^m+b_m-1x^m-1+... +b₁x+b_m≠0. Ясно, что ст. f (x) =n, а ст. g (x) =m. Нетрудно заметить, что если перемножить эти два многочлена, получится многочлен вида f (x) g (x) =a_nb_mx^m+n+... +a₀b₀. Так как a_n≠0 и b_n≠0, то a_nb_m≠0, а значит, ст. (f (x) g (x)) =m+n. Отсюда следует важное утверждение.

Степень произведения двух ненулевых многочленов равна сумме степеней сомножителей, или, короче, ст. (f (x) g (x)) =ст. f (x) +ст. g (x).

Легко доказать, что аналогичное утверждение имеет место для любого конечного числа ненулевых сомножителей, т.е. что ст. (f₁ (x) f₂ (x)... f_s (x)) = ст. f₁ (x) +ст. f₂ (x) +... +ст. f_s (x). Из рассуждений, приведенных выше для степени произведения двух многочленов, следует два полезных утверждения, которые легко распространяются на любое конечное число сомножителей.

Старший член (коэффициент) произведения двух ненулевых многочленов равен произведению старших членов (коэффициентов) сомножителей.

Свободный член произведения двух многочленов равен произведению свободных членов сомножителей.

Свойства

• Кольцо многочленов над произвольной областью целостности само является областью целостности.

• Кольцо многочленов от любого конечного числа переменных над любым факториальным кольцом само является факториальным.

• Кольцо многочленов от одного переменного над полем является кольцом главных идеалов, то есть любой его идеал может быть порожден одним элементом.

  • Более того, кольцо многочленов от одного переменного над полем является евклидовым кольцом.

Кольцо многочленов от одной переменной

Пусть — ассоциативное коммутативное кольцо с единицей. Рассмотрим множество бесконечных упорядоченных последовательностей , , в которых почти все элементы, кроме конечного числа, равны нулю. Две последовательности будем складывать по правилу:

.

Умножение зададим формулой

, где .

Предложение 1. Построенное множество с указанными операциями сложения и умножения является ассоциативным коммутативным кольцом с единицей. Нулевым элементом является нулевая последовательность , противоположным элементом для — элемент , единичным элементом — .

Последовательности при сложении и умножении ведут себя так же, как элементы кольца , поэтому вместо будем писать .

Обозначим

… … …

.

Тогда в новых обозначениях последовательность запишется в виде .

Определение 1. Построенное кольцо будем обозначать через и называть кольцом многочленов от одной переменной¹⁾, а его элемент — многочленом²⁾.

Замечание 1. Кольцо также называют алгеброй многочленов от одной переменной, имея ввиду, что определено умножение многочлена на скаляр по формуле

,

а значит, является алгеброй над кольцом .

Определение 2. Говорят, что степень многочлена³⁾ от одной переменной равна , если .

Предложение 2. Для любых двух многочленов справедливы неравенства:

1. ;

2. ;

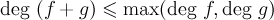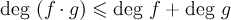3. если целостное, то .

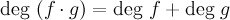Кольцо многочленов от n переменных

Пусть теперь — кольцо многочленов от одной переменной. Применяя вышеизложенную конструкцию, можно получить кольцо , которое обозначается через и называется кольцом многочленов от двух переменных. Элементы этого кольца имеют вид . Аналогично получается кольцо многочленов от трех переменных и т.д.

Определение 3. Вообще полученное таким способом кольцо называется кольцом многочленов от переменных. Элементы этого кольца — многочлены от переменных — имеют вид .

Определение 4. Выражения вида называются мономами⁴⁾. Степень монома . Степенью многочлена от переменных называется максимальная из степенй его мономов.

21. Нормальная форма записи многочленов. Степень многочлена и ее свойства. Кольцо многочленов над областью целостности.

Фробениусовой нормальной формой линейного оператора называется блочно-диагональная матрица, состоящая из фробениусовых клеток вида.

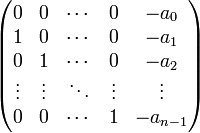
и является матрицей данного линейного оператора в некотором базисе.

Свойства

• Коэффициентами характеристического многочлена фробениусовой клетки являются 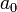, , 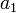, 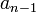из приведённой выше матрицы, и многочлен имеет вид .

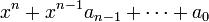Свойства

• Кольцо многочленов факториально: любой многочлен разлагается в произведение неприводимых многочленов, причем это разложение определено однозначно с точностью до постоянных множителей.

• Над полем вещественных чисел любой неприводимый многочлен одной переменной имеет степень 1 или 2, причем многочлен 2-й степени неприводим тогда и только тогда, когда он имеет отрицательный дискриминант.

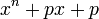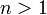• Над любым полем алгебраических чисел существуют неприводимый многочлен сколь угодно высокой степени; например, многочлен , где и 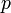― некоторое простое число, неприводим в силу критерия Эйзенштейна.

• Если 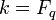— конечное поле из 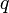элементов, а — натуральное число, то существует хотя бы один неприводимый многочлен степени n из .

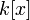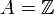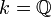• Предположим ― целозамкнутое кольцо с полем частных (например и ) и 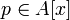― многочлен одной переменной со старшим коэффициентом 1, тогда 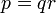в , причем и имеют старший коэффициент 1, то .

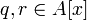• Редукционный критерий неприводимости. Пусть задан гомоморфизм областей целостности 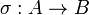. Если степень многочлена 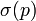совпадает со степенью многочлена и неприводим над полем частных области , то не существует разложения , где 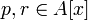и отличны от константы.

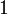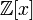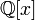  • Например, многочлен со старшим коэффициентом прост в (и, следовательно, неприводим в ), если прост многочлен , полученный из редукцией коэффициентов по модулю простого числа.

Область целостности (или целостное кольцо, или область цельности или просто область) — понятие абстрактной алгебры: ассоциативное коммутативное кольцо без делителя нуля (произведение ненулевых элементов не равно 0).

Эквивалентное определение: область целостности — это ассоциативное коммутативное кольцо, в котором нулевой идеал {0} является простым. Любая область целостности является подкольцом своего поля частных.

Примеры

• Простейший пример области целостности — кольцо целых чисел .

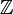• Любое поле является областью целостности. С другой стороны, любая артинова область целостности есть поле. В частности, все конечные области целостности суть конечные поля.

• Кольцо многочленов с коэффициентами из некоторого целостного кольца также является целостным. Например, целостными будут кольцо многочленов одной переменной с целочисленными коэффициентами и кольцо 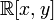многочленов двух переменных с вещественными коэффициентами.

• Множество действительных чисел вида 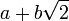есть подкольцо поля 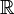, а значит, и область целостности. То же самое можно сказать про множество комплексных чисел вида 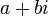, где и целые (множество Гауссовых целых).

• Пусть 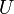— связное открытое подмножество комплексной плоскости 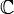. Тогда кольцо 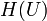всех голоморфных функций 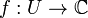будет целостным. То же самое верно для любого кольца аналитических функций, определённых на связном подмножестве аналитического многообразия.

• Если 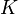— коммутативное кольцо, а 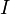— идеал в , то факторкольцо 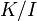целостное тогда и только тогда, когда — простой идеал.

22. Значение многочлена в точке. Деление с остатком. Две теоремы о делении с остатком. Схема Горнера.

Интерполяция алгебраическими многочленами функции f(x) на отрезке [a, b] — построение многочлена P_n(x) степени меньшей или равной n, принимающего в узлах интерполяции x₀, x₁, ..., x_n значения f(x_i):

Система уравнений, определяющих коэффициенты такого многочлена, имеет вид

Её определителем является определитель Вандермонда.

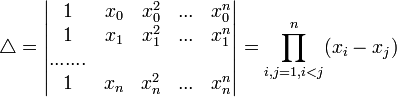
Он отличен от нуля при всяких попарно различных значениях x_i, и интерполирование функции f по её значениям в узлах x_i с помощью многочлена P_n(x) всегда возможно и единственно.

Деление c остатком (деление по модулю, нахождение остатка от деления, остаток от деления) — арифметическая операция, результатом которой является два целых числа: неполное частное и остаток от деления целого числа на другое целое число.

Определение

Разделить целое число на натуральное число с остатком означает представить его в виде:

При этом называется неполным частным, а — остатком от деления на

Например, при делении с остатком на получаем неполное частное и остаток

Деление с остатком

Определение. Пусть и — многочлены, . Будем говорить, что поделен на с остатком, если представлен в виде , где и — многочлены, причем .

Полином называется остатком от деления на , — неполным частным.

Пример. .

.

Теорема. (о делении с остатком). Пусть и — полиномы над полем , . Тогда существуют единственные многочлены и над полем такие, что и .

Доказательство. Существование.

Пусть . Положим .

.

Предположим, что теорема верна не для любого полинома ( фиксируем). Среди всех многочленов , для которых теорема неверна, выберем многочлен наименьшей степени и обозначим его :

Пусть . Положим

Коэффициент при в многочлене равен . Следовательно, . Значит, для многочлена теорема верна. Существуют такие и , что . Тогда

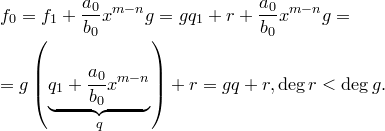
Получили противоречие с тем предположением, что есть многочлены, для которых теорема неверна.

Единственность. Предположим, что

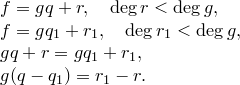
1) . Значит, ,

2) .

Получили противоречие. Этот случай невозможен.

Теорема Безу

Теорема. Остаток от деления многочлена на многочлен равен .

Доказательство. Степень остатка меньше 1, следовательно, остаток — константа. Пусть — остаток.

Это равенство верно при любых значениях . Положим :

Алгоритм Евклида для целых чисел

Пусть и — целые числа, не равные одновременно нулю, и последовательность чисел

определена тем, что каждое — это остаток от деления предпредыдущего числа на предыдущее, а предпоследнее делится на последнее нацело, то есть

Тогда НОД(a,b), наибольший общий делитель и , равен , последнему ненулевому члену этой последовательности.

Существование таких , то есть возможность деления с остатком на для любого целого и целого , доказывается индукцией по m.

Корректность этого алгоритма вытекает из следующих двух утверждений:

• Пусть 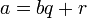, тогда НОД (a, b) = НОД (b, r).

• НОД(0, ) = для любого ненулевого (т.к. 0 делится на любое целое число, кроме нуля).

Проще сформулировать алгоритм Евклида так: если даны натуральные числа и и, пока получается положительное число, по очереди вычитать из большего меньшее, то в результате получится НОД.

Схе́ма Го́рнера (или правило Горнера, метод Горнера) — алгоритм вычисления значения многочлена, записанного в виде суммы мономов (одночленов), при заданном значении переменной. Метод Горнера позволяет найти корни многочлена^[1], а также вычислить производные полинома в заданной точке. Схема Горнера также является простым алгоритмом для деления многочлена на бином вида . Метод назван в честь Уильяма Джорджа Горнера (англ.).

Описание алгоритма

Задан многочлен :

.

Пусть требуется вычислить значение данного многочлена при фиксированном значении . Представим многочлен в следующем виде:

.

Определим следующую последовательность:

…

…

Искомое значение . Покажем, что это так.

В полученную форму записи подставим и будем вычислять значение выражения, начиная со внутренних скобок. Для этого будем заменять подвыражения через :

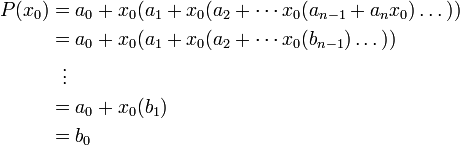
23. Теорема Безу. Корень многочлена, количество корней у многочлена. Теорема о тождестве. Алгебраически замкнутые поля, основная теорема алгебры (б/д). Разложение на линейные сомножители.

Теорема Безу утверждает, что остаток от деления многочлена на двучлен равен .

Предполагается, что коэффициенты многочлена содержатся в некотором коммутативном кольце с единицей (например, в поле вещественных или комплексных чисел).

Доказательство

Поделим с остатком многочлен на многочлен :

Так как , то — многочлен степени не выше 0. Подставляя , поскольку , имеем .

Корень многочлена

над полем k — элемент , который после подстановки его вместо x обращает уравнение

в тождество.

• Если c является корнем многочлена p(x), то p(x) делится без остатка на x − c (теорема Безу).

• Число вещественных корней многочлена с вещественными коэффициентами степени n заведомо меньше либо равно n. При этом комплексные корни многочлена (если они есть) сопряжены, таким образом, многочлен четной степени может иметь только четное число вещественных корней, а многочлен нечётной — только нечётное.

• Всякий многочлен p(x) с вещественными или комплексными коэффициентами имеет, по крайней мере, один, вообще говоря, комплексный корень (основная теорема алгебры).

  • То же верно для любого алгебраически замкнутого поля.

  • Более того многочлен p(x) можно записать в виде

где — (в общем случае комплексные) корни многочлена p(x), возможно с повторениями, при этом если среди корней многочлена p(x) встречаются равные, то общее их значение называется кратным корнем.

• Корни многочлена связаны с его коэффициентами формулами Виета

Теорема тождественности

В сложный анализ, теорема тождественности для голоморфные функции положения: дали функции f и g голоморфно на a соединено открытого множество D, если f = g на некотором районе z то внутри D, после этого f = g на D. Таким образом голоморфная функция вполне обусловлена своими значениями на районе a (по возможности довольно малого) внутри D. Это не поистине для реальн-differentiable функций. В сравнении, голоморфностью, или сложным-differentiability, будут очень более твердая придумка. Неофициально, иногда суммировать теорему путем говорить голоморфные функции «трудно» (в отличие от, мнение, непрерывные функции которые «мягки»).

Underpinning факт от теорема установлено developability голоморфной функции в свою серию портноя.

Доказательство

Предположение connectedness на домене D будет обязательно и будет в действительности ключево к скоро доказательству, котор дали здесь. (Очевидно если D consist of 2 disjoint открытого множество, результат не держит.) под этим предположением, в виду того что мы даемся что комплект не пуст, топологически сумма иска к тому f и g совпадите на комплекте оба открыто и закрыто. Closedness немедленно от непрерывность f и g.

Поэтому главный вопрос должен показать что комплект на f = g совпадите на открытого множество. Потому что голоморфная функция может быть представлена своим Серия портноя везде на своем домене, достаточно рассматривать комплект

Предположите w лож внутри S. После этого, потому что серия портноя f и g на w имейте non-zero радиус схождения, открытый диск B_r(w) также лежит внутри S для некоторого r. (В действительности, r может быть что-нибыдь чем расстояние от w к границе D). Это показывает S будет открыто и доказывает теорему.

Алгебраически замкнутое поле — поле , в котором всякий многочлен ненулевой степени над имеет хотя бы один корень.

Для любого поля существует единственное с точностью до изоморфизма его алгебраическое замыкание, то есть его алгебраическое расширение, являющееся алгебраически замкнутым.

Основна́я теоре́ма а́лгебры утверждает, что

Всякий отличный от константы многочлен с комплексными коэффициентами имеет по крайней мере один корень в поле комплексных чисел.

Эквивалентная формулировка теоремы следующая:

Поле комплексных чисел алгебраически замкнуто.

Следствие

Немедленным следствием из теоремы является то, что любой многочлен степени над полем комплексных чисел имеет в нём ровно корней, с учётом кратности корней.

Доказательство.

У многочлена есть корень , значит, по теореме Безу, он представим в виде , где — другой многочлен. Применим теорему к и будем применять её таким же образом до тех пор, пока на месте не окажется линейный множитель.

Доказательство.

Представим полином в виде суммы , где , . Составим соотношение . Легко видеть, что для любых коэффициентов всегда найдется такое значение , что для всех значений имеет место неравенство 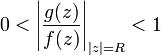. В силу теоремы Руше следует, что полное число нулей функции в круге равно числу нулей в этом круге функции . Но функция на всей комплексной плоскости имеет один единственный n-кратный корень . Отсюда, в силу произвольности и следует утверждение теоремы.

Тождественное преобразование, приводящее к произведению нескольких множителей - многочленов или одночленов, называют разложением многочлена на множители. В этом случае говорят, что многочлен делится на каждый из этих множителей.

• Вынесение общего множителя за скобки. Это преобразование является непосредственным следствием распределительного закона ac + bc = c(a + b)

• Пример. Разложить многочлен на множители 12 y ³ – 20 y ². Решение. Имеем: 12 y ³ – 20 y ² = 4 y ² · 3 y – 4 y ² · 5 = 4 y ² (3 y – 5). Ответ. 4 y ²(3 y – 5).

• Использование формул сокращенного умножения. Формулы сокращённого умножения позволяют довольно эффективно представлять многочлен в форме произведения.

• Пример. Разложить на множители многочлен x ⁴ – 1. Решение. Имеем: x ⁴ – 1 = ( x ² ) ² – 1 ² = ( x ² – 1)( x ² + 1) = ( x ² – 1 ² )( x ² + 1) = ( x + 1)( x – 1)( x ² + 1). Ответ. ( x + 1)( x – 1)( x ² + 1).

• Способ группировки. Этот способ заключается в том, что слагаемые многочлена можно сгруппировать различными способами на основе сочетательного и переместительного законов. На практике он применяется в тех случаях, когда многочлен удается представить в виде пар слагаемых таким образом, чтобы из каждой пары можно было выделить один и тот же множитель. Этот общий множитель можно вынести за скобку и исходный многочлен окажется представленным в виде произведения.

• Пример. Разложить на множители многочлен x ³ – 3 x ² y – 4 xy + 12 y ². Решение. Сгруппируем слагаемые следующим образом: x ³ – 3 x ² y – 4 xy + 12 y ² = ( x ³ – 3 x ² y ) – (4 xy – 12 y ² ). В первой группе вынесем за скобку общий множитель x ², а во второй − 4 y . Получаем: ( x ³ – 3 x ² y ) – (4 xy – 12 y ² ) = x ² ( x – 3 y ) – 4 y ( x – 3 y ). Теперь общий множитель ( x – 3 y ) также можно вынести за скобки: x ² ( x – 3 y ) – 4 y ( x – 3 y ) = ( x – 3 y )( x ² – 4 y ). Ответ. ( x – 3 y )( x ² – 4 y ).

• Способ выделения полного квадрата. Метод выделения полного квадрата является одним из наиболее эффективных методов разложения на множители. Суть его состоит в выделении полного квадрата и последующего применения формулы разности квадратов.

• Пример. Разложить на множители многочлен x ⁴ + 4 x ² – 1. Решение. Имеем x4+4x2−1=x4+2 2x2+4−4−1=(x2+2)2−5=(x2+2− 5)(x2+2− 5) .

24. Решение уравнений третьей степени.

25.Решение уравнений четвертой степени.

Уравнение четвёртой степени — в математике алгебраическое уравнение вида:

Четвёртая степень для алгебраических уравнений является наивысшей, при которой существует аналитическое решение в радикалах в общем виде (то есть при любом значении коэффициентов).

Так как является многочленом чётной степени, она имеет один и тот же предел при стремлении к плюс и к минус бесконечности. Если , то функция возрастает до плюс бесконечности с обеих сторон, таким образом, функция имеет глобальный минимум. Аналогично, если , то функция убывает до минус бесконечности с обеих сторон, таким образом, функция имеет глобальный максимум

Теорема Виета для уравнения четвертой степени

Корни уравнения четвертой степени связаны с коэффициентами следующим образом:

Решение уравнений четвертой степени по методу Феррари.

В общем случае, приведенное уравнение четвертой степени вида можно решить методом Феррари. Находится - любой из корней кубического уравнения (см. решение кубических уравнений). Затем решаются два квадратных уравнения подкоренное выражение является полным квадратом. Корни этих уравнений являются корнями исходного уравнения четвертой степени.

26. НОД. Единственность НОДа и его линейное представление. Алгоритм Евклида и нахождение линейного представления НОДа.

Наибольшим общим делителем (НОД) для двух целых чисел m и n называется наибольший из их общих делителей.^[1] Пример: для чисел 70 и 105 наибольший общий делитель равен 35.

Наибольший общий делитель существует и однозначно определён, если хотя бы одно из чисел m или n не ноль.

Возможные обозначения наибольшего общего делителя чисел m и n:

• НОД(m, n)

• (m, n)

• gcd(m, n) (от англ. Greatest Common Divisor)

Понятие наибольшего общего делителя естественным образом обобщается на наборы из более чем двух целых чисел.

Теорема. Пусть – целые числа, НОД . Число можно представить в виде

— целые числа

Доказательство. Пусть — множество всех чисел, которые можно получить из и с помощью сложения и вычитания. Тогда, если , то . Так как в алгоритме Евклида

то

Но .

Следствия.

1. НОД двух чисел делится на любой общий делитель этих чисел.

2. Уравнение , где — целые коэффициенты, — целочисленные неизвестные, разрешимо в том и только в том случае, если делится на НОД .

Алгоритм Евклида для целых чисел

Пусть и — целые числа, не равные одновременно нулю, и последовательность чисел

определена тем, что каждое — это остаток от деления предпредыдущего числа на предыдущее, а предпоследнее делится на последнее нацело, то есть

Тогда НОД(a,b), наибольший общий делитель и , равен , последнему ненулевому члену этой последовательности.

Существование таких , то есть возможность деления с остатком на для любого целого и целого , доказывается индукцией по m.

Корректность этого алгоритма вытекает из следующих двух утверждений:

• Пусть , тогда НОД (a, b) = НОД (b, r).

Доказательство

1. Пусть k — любой общий делитель чисел a и b, не обязательно наибольший, тогда 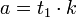; 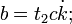где и 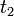— целые числа из определения.

2. Тогда k является также общим делителем чисел b и r, так как b делится на k по определению, а 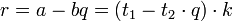(выражение в скобках есть целое число, следовательно, k делит r без остатка)

3. Обратное также верно и доказывается аналогично пункту 2: любой делитель b и r так же является делителем a и b.

4. Следовательно, все общие делители пар чисел (a, b) и (b, r) совпадают. Другими словами, нет общего делителя у чисел (a, b), который не был бы также делителем (b, r), и наоборот.

5. В частности, наибольший общий делитель остается тем же самым. Что и требовалось доказать.

• НОД(0, ) = для любого ненулевого (т.к. 0 делится на любое целое число, кроме нуля).

Проще сформулировать алгоритм Евклида так: если даны натуральные числа и и, пока получается положительное число, по очереди вычитать из большего меньшее, то в результате получится НОД.

27. Взаимно простые многочлены. Определение, свойства

Т. Критерий взаимной простоты. Для того, чтобы многочлены f(x) и g(x) из F[x] были взаимно простыми, необходимо и достаточно, чтобы в F[x] существовали такие u(x) и v(x), что u(x)f(x)+v(x)g(x)=1. Док-во: - Необходимость: очевидно. - Достаточность: Пусть d(x) - НОД многочленов f(x) и g(x). Значит каждое из слагаемых левой части делится на d(x). А значит и правая часть делится на d(x). Следовательно d(x) - ненулевая константа. Свойства взаимно простых многочленов. Т. Если многочлен f(x) взаимно прост с каждым из многочленов g(x) и h(x), то он взаимно прост и с их произведением. Док-во: Из условия следует, что найдутся такие u(x), v(x), u1(x), v1(x), что: u(x)f(x)+v(x)g(x)=1 u1(x)f(x)+v1(x)h(x)=1. Складывая эти неравенства, получим: (u(x)u1(x)f(x)+u(x)v1(x)h(x)+v(x)g(x)u1(x))*f(x) + (v(x)v1(x))*g(x)h(x) = 1 Т. f(x)h(x):g(x), НОД(f(x),g(x))=1 ===> h(x):g(x). Док-во: u(x)f(x)+v(x)g(x)=1 u(x)f(x)h(x)+v(x)g(x)h(x)=h(x) 1-ое слагаемое делится на g(x) по условию, второе - очевидно. След-но правая часть делится на g(x). Т. f(x):g(x), f(x):h(x), НОД(g,h)=1, ===> f(x):g(x)h(x). Док-во: Сущ. q(x) такое, что f(x)=q(x)g(x) ===> q(x):h(x). Сущ. q1(x) такое, что q(x)=q1(x)h(x) ===> f(x)=q1(x)g(x)h(x).

28. Неприводимые многочлены. Определение, свойства.

Неприводимый многочлен — многочлен, неразложимый на нетривиальные (неконстантные) многочлены. Неприводимые многочлены являются неприводимыми элементами кольца многочленов.

Определение

Неприводимый многочлен над полем ― многочлен от переменных над полем является простым элементом кольца , то есть, непредставим в виде произведения , где и ― многочлены с коэффициентами из , отличные от констант.

Многочлен называется абсолютно неприводимым, если он неприводим над алгебраическим замыканием поля коэффициентов. Абсолютно неприводимые многочлены одной переменной ― это многочлены 1-й степени и только они. В случае нескольких переменных существуют абсолютно неприводимые многочлены сколь угодно высокой степени — например, любой многочлен вида

абсолютно неприводим.

Свойства

• Кольцо многочленов факториально: любой многочлен разлагается в произведение неприводимых многочленов, причем это разложение определено однозначно с точностью до постоянных множителей.

• Над полем вещественных чисел любой неприводимый многочлен одной переменной имеет степень 1 или 2, причем многочлен 2-й степени неприводим тогда и только тогда, когда он имеет отрицательный дискриминант.

• Над любым полем алгебраических чисел существуют неприводимый многочлен сколь угодно высокой степени; например, многочлен , где и ― некоторое простое число, неприводим в силу критерия Эйзенштейна.

• Если — конечное поле из элементов, а — натуральное число, то существует хотя бы один неприводимый многочлен степени n из .

• Предположим ― целозамкнутое кольцо с полем частных (например и ) и ― многочлен одной переменной со старшим коэффициентом 1, тогда в , причем и имеют старший коэффициент 1, то .

• Редукционный критерий неприводимости. Пусть задан гомоморфизм областей целостности . Если степень многочлена совпадает со степенью многочлена и неприводим над полем частных области , то не существует разложения , где и отличны от константы.

Например, многочлен со старшим коэффициентом прост в (и, следовательно, неприводим в ), если прост многочлен , полученный из редукцией коэффициентов по модулю простого числа.

29. Каноническое разложение многочлена на неприводимые многочлены.

Рассмотрим самый общий случай. Пусть дано некоторое поле многочленов GF(q), где q = pⁿ, n — степень модуля q, а p — характеристика. Обозначим через g₁(x), g₂(x), ..., g_q–1(x) различные неприводимые многочлены над полем чисел GF(p), отвечающие примитивным корням: c₁, c₂, ... , c_{q –1}. Утверждается, что существует единственно возможное разложение многочлена x^q–1 – 1 на множители g_i(x); или, что одно и то же, каждый элемент c_i является корнем многочлена x^q–1 – 1; или, наконец, исходный приводимый многочлен можно представить в виде произведения порождающего g(x) и проверочного h(x) многочленов:

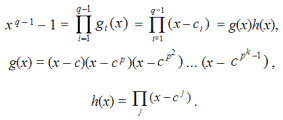
Здесь c — примитивный корень порождающего многочлена g(x), а для проверочного многочлена h(x) берутся те степени c ^j, которые не вошли в многочлен g(x). Как видим, действия с многочленами во многом схожи с действиями над числами. Приводимый многочлен вида x^q–1 – 1 играет роль составного числа a, его примитивные корни c₁, c₂, ... , c_{q –1} ассоциируются с простыми сомножителями p₁, p₂, ..., p_k, а последняя формула разложения на множители аналогична каноническому разложению составного числа a = p₁ⁿ¹ p₂ⁿ² ....p_k^nk. Многочлены g(x) и h(x) играют роль двух делителей числа a = g · h. Корни исходного многочлена играют роль базиса, по которому многочлены g(x) и h(x) могут быть разложены. Таким образом, теория полей многочленов смыкается с теорией линейных пространств. Покажем, как это осуществляется практически.

Если c — примитивный корень многочлена g(x), то

g(c) = g₀ + g₁c + g₂c² + ... + g_ncⁿ = 0.

Выразим степени корней cⁿ и cⁿ⁺¹ через линейную комбинацию младших степеней корней c, c², ..., c^n–1 (g_n = 1):

cⁿ = g₀ + g₁c + g₂c² + ... + g_n–1c^n–1,

cⁿ⁺¹ = g₀c + g₁c² + g₂c³ + ...

... + g_n–1(g₀ + g₁c + g₂c² + ... + g_n–1c^n–1).

Следовательно, все степени cⁱ при i > n линейно выражаются через первые n степеней; число таких комбинаций не превышает величину q – 1. Следует также иметь в виду, что не только g(c) = 0, но и

g(c²) = g(c³) = ... = g(c^q–1) = 0.

29. Неприводимые многочлены над полями комплексных и вещественных чисел.

Следующие пять многочленов демонстрируют некоторые элементарные свойства неприводимых многочленов:

,

,

,

,

.

Над кольцом целых чисел, первые два многочлена — приводимые, последние два — неприводимые. (Третий вообще не является многочленом над целыми числами).

Над полем рациональных чисел, первые три многочлена являются приводимыми, двое других — неприводимыми.

Над полем действительных чисел, первые четыре многочлена — приводимые, но является неприводимым. В поле действительных чисел неприводимыми являются линейные многочлены и квадратичные многочлены без действительных корней. Например разложение многочлена в поле действительных чисел имеет вид . Оба множителя в данном разложении являются неприводимыми многочленами.

Над полем комплексных чисел, все пять многочленов — приводимые. Фактически, каждый отличный от константы многочлен над может быть разложен на множители вида:

где — степень многочлена, — старший коэффициент, — корни . Поэтому единственными неприводимыми многочленами над являются линейные многочлены (основная теорема алгебры).

Конечные поля

Многочлены с целочисленными коэффициентами, которые являются неприводимыми над полем могут быть приводимыми над конечным полем. Например, многочлен является неприводимым над , но над полем из двух элементов мы имеем:

31. Многочлены от нескольких переменных. Симметрические многочлены. Теорема о симметрических многочленах.

Возьмем две буквы x и y. Произведение где а – число, называется одночленом. Его степень равна k+l. Сумма одночленов называется многочленом. В отличие от многочленов с одной переменной, для многочленов с большим числом переменных нет общепринятой стандартной записи. Так же, как и многочлены от одной переменной, многочлены от двух переменных могут раскладываться на множители. Важным разложением является разложение разности n-ых степеней, которое вам известно для n=2 и 3: Эти формулы легко обобщаются для произвольного n: Сумма n-ых степеней легко раскладывается в случае, когда n нечетно. Слагаемое можно представить в виде и воспользоваться формулой разложения разности n-ых степеней.

Симметричные многочлены Среди многочленов от двух переменных важную роль играют симметричные многочлены, т. е. многочлены, не меняющиеся при перестановке букв x и y.

Симметри́ческий многочле́н — многочлен от n переменных , не изменяющийся при всех перестановках входящих в него переменных.

Примеры

• Дискриминант — многочлен вида , где — корни некого многочлена от одной переменной: .

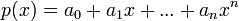• Степенные суммы — суммы одинаковых степеней переменных, то есть

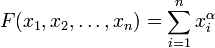
• Основные симметрические многочлены — многочлены вида

определённые для , то есть такие:

70