
- •Группы, кольца, поля. Определения и примеры. Кольца из 2-5 элементов. Область целостности.
- •Комплексные числа. Определение, нормальная форма. Поле комплексных чисел.
- •Комплексные числа на плоскости. Модуль и аргумент числа, тригонометрическая форма. Сопряженные числа и их свойства.
- •Произведение комплексных чисел в тригонометрической форме. Возведение числа в степень и извлечение корня.
- •7. Векторные пространства. Определение и примеры. Свойства нуля. Линейное выражение.
- •8. Линейно зависимые и линейно независимые системы векторов. Свойства. Порождающие системы векторов. Примеры. Линейно зависимые и линейно независимые системы векторов
- •9. Базис. Теорема о базисе. Количество векторов в базисе. Размерность и ранг. Примеры. Координаты вектора в базисе.
- •10. Матрицы. Определение матрицы. Сложение матриц, умножение матрицы на число и транспонирование матрицы. Их свойства.
- •11. Умножение матриц. Свойства, примеры.
- •Запись системы линейных уравнений в матричном виде. Связь между изменением базиса и матрицами. Двойное изменение базиса. Координаты вектора в новом базисе.
- •Изменение координат вектора при изменении базиса
- •Элементарные преобразования в матричном виде. Теорема о ранге матрицы.
- •Инвариантность ранга при элементарных преобразованиях
- •Эквивалентность слау при элементарных преобразованиях
- •Свойства ранга матрицы. Связь с обратными матрицами. Теорема Кронекера-Капелли.
- •Свойства
- •Необходимость
- •Достаточность
- •Следствия
- •15. Перестановки. Произведение перестановок. Транспозиция. Перестановка как произведение транспозиций и транспозиция как произведение транспозиций соседних элементов.
- •16. Инверсии в перестановке. Четность перестановки. Связь с транспозициями. Четность произведения перестановок.
- •17. Определение определителя. Определители небольших порядков. Начальные свойства (1-6).
- •18. Дальнейшие свойства. Алгебраическое дополнение и минор. Разложение по строке. Примеры.
- •19. Теорема Крамера. Нахождение обратной матрицы с помощью определителей. Определитель произведения.
- •§2 Свойства умножения матриц
- •20.Определение многочлена от одной переменной. Действия с многочленами и их свойства. Пространство и кольцо многочленов.
- •21. Нормальная форма записи многочленов. Степень многочлена и ее свойства. Кольцо многочленов над областью целостности.
- •22. Значение многочлена в точке. Деление с остатком. Две теоремы о делении с остатком. Схема Горнера.
- •Деление с остатком
- •Теорема Безу
- •23. Теорема Безу. Корень многочлена, количество корней у многочлена. Теорема о тождестве. Алгебраически замкнутые поля, основная теорема алгебры (б/д). Разложение на линейные сомножители.
- •24. Решение уравнений третьей степени.
- •25.Решение уравнений четвертой степени.
- •27. Взаимно простые многочлены. Определение, свойства
- •29. Неприводимые многочлены над полями комплексных и вещественных чисел.
- •31. Многочлены от нескольких переменных. Симметрические многочлены. Теорема о симметрических многочленах.
Алгебраические структуры
Множества. Декартово произведение и декартова степень. Отображения множеств. Алгебраические операции. Примеры.
Множество - это совокупность, класс отличающихся друг от друга объектов, объединенных каким-либо общим свойством. Объекты, входящие в эту совокупность, называются элементами множества.
Множества обозначаются заглавными буквами латинского алфавита , а элементы множества- строчными.
Приведем примеры множеств.
Классы (множества) чисел: N – натуральные числа, Z – целые числа, Q- рациональные числа, R- действительные (вещественные) числа, C – комплексные числа.
Студенты одной группы – множество, элементы которого- студенты, общее свойство – обучение одной специальности.
Множество В – корни уравнения ½ = cosx . Элементы – вещественные числа, общее свойство – обращают данное уравнение в верное равенство.
Если х – элемент множества Х, то говорят: х принадлежит Х и пишут : хХ. Если х не принадлежит Х, то пишут хХ.
С видами множеств вы знакомились при изучении элементов высшей математики, поэтому лишь напомним их : конечные множества, бесконечные, пустые, универсальные.
Конечные и бесконечные множества в свою очередь подразделяются на неупорядоченные и упорядоченные; неупорядоченные бесконечные – на счетные и несчетные.
Операции над множествами
Основными операциями над множествами являются объединение, пересечение и разность.
Определение 1. Объединением двух множеств называется новое множество
![]()
Определение 2. Пересечением двух множеств называется новое множество
![]()
Определение 3. Разностью двух множеств называется новое множество
![]()
Если класс объектов, на которых
определяются различные множества
обозначить
![]() (Универсум),
то дополнением множества
(Универсум),
то дополнением множества
![]() называют
разность
называют
разность
![]()
Декартово произведение множеств
Одним из способов конструирования новых объектов из уже имеющихся множеств является декартово произведение множеств.
Пусть
и
![]() -
множества. Выражение вида
-
множества. Выражение вида
![]() ,
где
,
где
![]() и
и
![]() ,
называется упорядоченной парой.
Равенство вида
,
называется упорядоченной парой.
Равенство вида
![]() означает,
что
означает,
что
![]() и
и
![]() .
В общем случае, можно рассматривать
упорядоченную n-ку
.
В общем случае, можно рассматривать
упорядоченную n-ку
![]() из
элементов
из
элементов
![]() .
Упорядоченные n-ки иначе называют наборы
или кортежи.
.
Упорядоченные n-ки иначе называют наборы
или кортежи.
Определение 4. Декартовым (прямым)
произведением множеств
![]() называется
множество упорядоченных n-ок (наборов,
кортежей) вида
называется
множество упорядоченных n-ок (наборов,
кортежей) вида
![]()
Определение 5. Степенью декартового
произведения
![]() называется
число множеств n, входящих в это декартово
произведение.
называется
число множеств n, входящих в это декартово
произведение.
Замечание. Если все множества
![]() одинаковы,
то используют обозначение
одинаковы,
то используют обозначение
![]() .
.
Прямое или декартово произведение — множество, элементами которого являются всевозможные упорядоченные пары элементов исходных двух множеств. Данное понятие употребляется не только в теории множеств, но также в алгебре, топологии и прочих разделах математики благодаря тому, что прямое произведение часто наследует структуры (алгебраические, топологические и т. д.), существующие на перемножаемых множествах.
Декартова степень
![]() -я
Декартова степень множества
-я
Декартова степень множества
![]() определяется
для целых
неотрицательных
,
как
-кратное
Декартово произведение
на
себя:
определяется
для целых
неотрицательных
,
как
-кратное
Декартово произведение
на
себя:
![]()
Группы, кольца, поля. Определения и примеры. Кольца из 2-5 элементов. Область целостности.
Комплексные числа. Определение, нормальная форма. Поле комплексных чисел.
Введение понятия комплексного числа. Представление комплексного числа на плоскости
Комплексные числа
являются расширением множества
действительных чисел. В результате
расширения множества действительных
чисел было введено понятие мнимой
единицы
![]() ,
которая существует на множестве
комплексных чисел, но не существует на
множестве действительных. Мнимая единица
удовлетворяет равенству:
,
которая существует на множестве
комплексных чисел, но не существует на
множестве действительных. Мнимая единица
удовлетворяет равенству:
|
(1) |
В литературе часто
мнимую единицу обозначают через
![]() .
Тогда комплексное число
.
Тогда комплексное число
![]() можно
представить в виде:
можно
представить в виде:
|
(2) |
где
![]() носит
название действительной части или
реальной части и обозначается
носит
название действительной части или
реальной части и обозначается
![]() ,
а
,
а
![]() носит
название мнимой части и обозначается
как
носит
название мнимой части и обозначается
как
![]() .
Графически все множество действительных
чисел можно представить на бесконечной
числовой прямой, при этом комплексные
числа можно трактовать как расширение
числовой прямой до комплексной плоскости,
а каждое комплексное число можно
представить как точку на комплексной
плоскости (смотри рисунок 1). При этом
все множество действительных чисел
будет представляться прямой на комплексной
плоскости.
.
Графически все множество действительных
чисел можно представить на бесконечной
числовой прямой, при этом комплексные
числа можно трактовать как расширение
числовой прямой до комплексной плоскости,
а каждое комплексное число можно
представить как точку на комплексной
плоскости (смотри рисунок 1). При этом
все множество действительных чисел
будет представляться прямой на комплексной
плоскости.
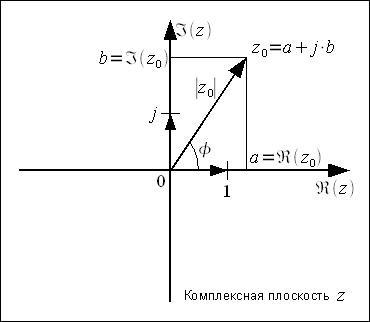 Рисунок
1: Представление комплексного числа на
плоскости
Рисунок
1: Представление комплексного числа на
плоскости
Комплексная
плоскость
делится
прямыми реальной части
![]() (прямой
действительных чисел) и прямой мнимых
чисел
(прямой
действительных чисел) и прямой мнимых
чисел
![]() на
четыре четверти. Любое комплексное
число
на
четыре четверти. Любое комплексное
число
![]() ,будет
представляться точкой на комплексной
плоскости с координатами
,будет
представляться точкой на комплексной
плоскости с координатами
![]() и
и
![]() .
Если число не содержит мнимой части, то
оно действительное и находится на прямой
,
а если число не содержит реальной части,
то оно называется чисто мнимым и находится
на оси
.
.
Если число не содержит мнимой части, то
оно действительное и находится на прямой
,
а если число не содержит реальной части,
то оно называется чисто мнимым и находится
на оси
.
Такое расширение должно «наследовать» все свойства вещественных чисел, т.е. в этом множестве операции должны подчиняться аксиомам коммутативности, ассоциативности и дистрибутивности:
1.![]() ;
;
2.![]() ;
;
3.![]() ;
;
4.![]() ;
;
5.![]() ;
;
6.существует
нейтральный элемент
![]() относительно
сложения:
относительно
сложения:
![]() ;
;
7.существует
нейтральный элемент
![]() относительно
умножения:
относительно
умножения:
![]() .
.
Все указанные равенства должны выполняться
для произвольных чисел
![]() .
.
производится отождествление
комплексного числа
![]() с
вещественным числом
с
вещественным числом
![]() .
Результатом этого является следующая
нормальная форма записи комплексного
числа
.
Результатом этого является следующая
нормальная форма записи комплексного
числа
![]()
Для числа
![]() получаем
одно определяющее равенство:
получаем
одно определяющее равенство:
![]()
Из соображений упрощения записи,
договорились число
![]() записывать
просто в виде
записывать
просто в виде
![]() ,
а числа
,
а числа
![]() и
и
![]() записывать
в виде
записывать
в виде
![]() и
и
![]() .
.
Польза от нормальной формы записи состоит в том, что она упрощает действия с комплексными числами. В самом деле, перемножение двух комплексных чисел, представленных в нормальной форме,можно начать производить по обычным правилам перемножения вещественных чисел:
![]()
а затем воспользоваться равенством
![]() :
:
![]()
Мы получили тот же результат, что формально определен аксиомой.
Если
![]() —
целое число, то число
—
целое число, то число
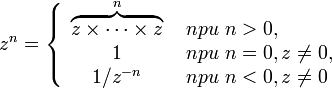
называется
![]() -й
степенью числа
-й
степенью числа
![]() .
.
Для вычисления
![]() при
при
![]() и
и
![]() можно
применить формулу бинома
Ньютона:
можно
применить формулу бинома
Ньютона:
![]()
Определение 1. Алгебраическое
расширение поля
действительных
чисел
![]() с
помощью элемента
с
помощью элемента
![]() ,
являющегося корнем
многочлена
,
являющегося корнем
многочлена
![]() ,
называется полем комплексных чисел1).
Поле комплексных чисел обозначается
через
,
называется полем комплексных чисел1).
Поле комплексных чисел обозначается
через
![]() .
.
Предложение 1. Каждое ассоциативное
коммутативное кольцо
![]() с
единицей и без делителей
нуля, являющееся двумерным
векторным
пространством над полем
,
изоморфно полю
.
с
единицей и без делителей
нуля, являющееся двумерным
векторным
пространством над полем
,
изоморфно полю
.
Теорема 1.(Основная теорема алгебры.) Поле комплексных чисел алгебраически замкнуто.
Определение 2. Полем комплексных
чисел
называется
множество всех упорядоченных пар
действительных чисел
![]() .
При этом каждая такая пара
.
При этом каждая такая пара
![]() называется
комплексным числом2).
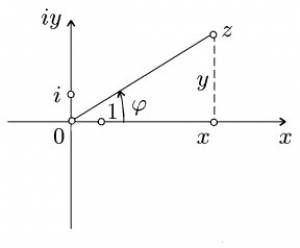
Таким образом, множество комплексных
чисел можно интерпретировать как точки
на плоскости
называется
комплексным числом2).
Таким образом, множество комплексных
чисел можно интерпретировать как точки
на плоскости
![]() .
.
 Определим
операцию сложения комплексных чисел
по правилу
Определим
операцию сложения комплексных чисел
по правилу
![]() для
всех
для
всех
![]() ,
,
и определим операцию умножения:
![]() для
всех
.
для
всех
.
