
- •Лекция 1
- •Мир не линеен и поэтому сложен.
- •Основное свойство:
- •Линейное свойство:
- •Лекция 3
- •Лекция 4
- •Лекция 6 лекция 7
- •Лекция 8
- •Лекция 9
- •Лекция 10 лекция 11
- •Свойства подобных матриц.
- •Лекция 12
- •Лекция 13 лекция 14
- •Лекция 15
- •Лекция 16
- •Программа по линейной алгебре для студентов 1 курса физического факультета
- •I. Матрицы и определители
- •II. Линейные пространства
- •III. Системы линейных уравнений
- •IV. Евклидовы и унитарные пространства.
- •V. Линейные операторы в конечномерном пространстве.
- •VI. Билинейные и квадратичные формы. Функции от матриц.
- •Д.К.Фаддеев ”Лекции по алгебре” 2005г.
- •1. Проскуряков м.В.: - Сборник задач по линейной алгебре
- •2.Фаддеев д.К., Соминский и.С.: - Задачи по высшей алгебре
Лекция 9
Продолжение лекции 8
-
«…И только теперь, когда ты вышел из берегов, увидел океан и познал свое ничтожество, с тобой можно говорить о великой истине»
Из беседы духа океана с духом реки в момент разлива реки.
3 , мерное комплексное евклидово пространство.
![]() .
.
Общий вид задания скалярного произведения в
Рассмотрим два
вектора
![]() и
и
![]()
![]() ,
координаты
векторов комплексные числа.
,
координаты
векторов комплексные числа.
![]() ,
,
Первое условие.
Так как, согласно первой аксиоме
![]() ,
то имеем следующие соотношения
,
то имеем следующие соотношения
![]() ,
,
![]()
![]()
![]() ,
,
![]()
![]() , (
)
, (
)
Следовательно,
![]() ,
т.е.
,
т.е.
![]() -
матрица экмитовая.
-
матрица экмитовая.
Здесь мы ввели обозначение звездочку * - это знак эрмитова сопряжения.
Второе условие. Так как, согласно четвертой аксиоме , то
![]()
Следовательно, матрица должна определять положительно-определенную полуторалинейную форму.
4
![]() ,
множество функций, определенных на
отрезке
,
множество функций, определенных на
отрезке
![]() .
.
![]() ,
т.е. пространство бесконечноменое.
Рассмотрим две функции
,
т.е. пространство бесконечноменое.
Рассмотрим две функции
![]() и
и
![]() ,
,
![]() .
Определим скалярное произведение,
используя определенный интеграл
.
Определим скалярное произведение,
используя определенный интеграл
![]() .
Это простейший случай задания.
.
Это простейший случай задания.
В общем случае скалярное произведение имеет вид
![]() ,
где функция
,
где функция
![]() положительна на отрезке
.
Эта функция называется функцией
распределения, или весовой функцией.
Все аксиомы выполнены.
положительна на отрезке
.
Эта функция называется функцией
распределения, или весовой функцией.
Все аксиомы выполнены.
Неравенство Коши
–Буняковского
:
![]()
Докажем неравенство для случая вещественного линейного пространства.
Рассмотрим векторы
![]() и
и
![]() и их линейную комбинацию
и их линейную комбинацию
![]() ,
,
![]() .
Имеем
.
Имеем
![]()
Это неравенство принимает лишь неотрицательные значения при любом . Следовательно, дискриминант не может быть положительным:
![]() .
Что и требовалось доказать.
.
Что и требовалось доказать.
Следствие. Из неравенства Коши – Буняковского следует неравенство
![]() .
.
Извлекаем из этого выражения квадратный корень и получаем
![]() , где
, где
![]() - длина вектора
.
- длина вектора
.
Введем
![]() , где
, где
![]() угол между векторами . Это можно сделать,
так как выполняется очевидное условие.
угол между векторами . Это можно сделать,
так как выполняется очевидное условие.
![]() .
.
Определение.
Линейное пространство, в котором введена
длина вектора
![]() ,
называется нормированным пространством,
если выполнены три условия:
,
называется нормированным пространством,
если выполнены три условия:

 - неравенство
треугольника.
- неравенство
треугольника.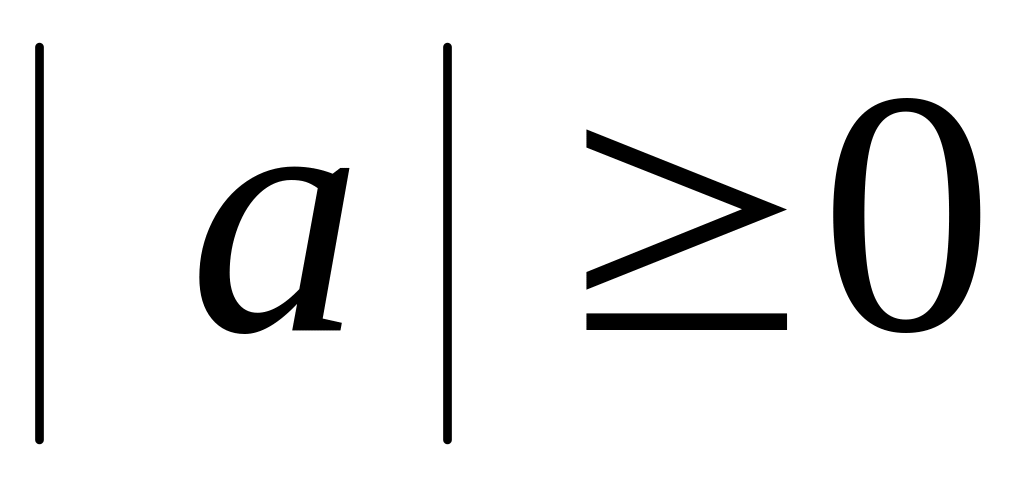
Любое евклидово пространство всегда является нормированным пространством, так как длину вектора всегда можно определить как квадратный корень из скалярного произведения . При этом все три условия выполняются. Чтобы убедиться в этом, решите следующую задачу.
Задача. Доказать неравенство треугольника, используя неравенство Коши_Буняковского
Лекция 10 лекция 11
Инвариантное подпространство. Собственный вектор и собственное значение линейного оператора. Характеристическое уравнение. Структура линейного оператора. Спектр линейного оператора.
-
«Право на левой стороне»
Инвариантное подпространство. Собственный вектор и собственное значение линейного оператора. Характеристическое уравнение. Структура линейного оператора.
Поставим следующий вопрос: Как, и каким образом, мы можем изучить устройство или структуру линейного оператора?
Ответ:
структура
линейного оператора полностью определяется
структурой
(или видом) матрицы линейного оператора.
Речь идет о
приведение матрицы
![]() линейного оператора
линейного оператора
![]() к наиболее простому виду при
помощи выбора базиса.
Очевидно, наиболее простой матрицей
является диагональная матрица. Возникает
вопрос, как найти этот базис?
к наиболее простому виду при
помощи выбора базиса.
Очевидно, наиболее простой матрицей
является диагональная матрица. Возникает
вопрос, как найти этот базис?
Центральное
место в решении этой задачи занимает
понятие инвариантного
подпространства,
в особенности, одномерного
инвариантного подпространства.
Интересная
и плодотворная картина структуры
линейного оператора возникает для
случая, когда линейный оператор производит
отображение линейного пространства в
себя
![]() .
.
Итак,
рассмотрим в линейном пространстве
некоторое подпространство
![]() ,
,
![]() .
Пусть
линейный оператор, действующий в
.
.
Пусть
линейный оператор, действующий в
.
Определение.
Пусть
линейный оператор в
.
Подпространство
называется
инвариантным
относительно действия оператора
,
если для каждого вектора
из
вектор
![]() также принадлежит
.
также принадлежит
.
Или:
Подпространство
инвариантно
относительно действия оператора
,
если
![]()
Примеры инвариантных подпространств.
1.Нульмерное
пространство (пространство, состоящее
из нулевого вектора Пусть
![]() и
и
![]() .
.
2.Все пространство
:
![]() и
и
![]() .
.
3. Ядро линейного
оператора
![]() :
:
![]() и
и
![]() .
.
4. Образ линейного
оператора
![]() :
:
![]() и
и
![]() .
.
Особую роль играют одномерные инвариантные подпространства в .
Пусть
![]() - одномерное инвариантное подпространство.
В силу одномерности
,
очевидно, что вектор
- одномерное инвариантное подпространство.
В силу одномерности
,
очевидно, что вектор
![]() пропорционален
для каждого вектора
пропорционален
для каждого вектора![]() :
:
![]() ,
где
,
где
![]() -
коэффициент пропорциональности.
-
коэффициент пропорциональности.
Определение.
Вектор
![]() ,
удовлетворяющий соотношению
,
называется собственным вектором, а
число
-
собственным значением линейного
оператора
.
,
удовлетворяющий соотношению
,
называется собственным вектором, а
число
-
собственным значением линейного
оператора
.
Итак, если
- собственный вектор, то векторы
![]() образуют одномерное инвариантное
подпространство (линейная оболочка).
Обратно, любой вектор одномерного
инвариантного подпространства является
собственным вектором.
образуют одномерное инвариантное
подпространство (линейная оболочка).
Обратно, любой вектор одномерного
инвариантного подпространства является
собственным вектором.
Зададим вопрос: Может ли существовать собственный вектор линейного оператора? Ответ дает следующая теорема.
ТЕОРЕМА. Всякий линейный оператор имеет, по крайней мере, один собственный вектор.
Доказательство. Предположим, что существует вектор : .
Выберем в
базис
.
Линейному оператору
в этом базисе соответствует некоторая
матрица
![]() :
:
![]() .
Тогда операторному соотношению
будет соответствовать матричное
соотношение:
.
Тогда операторному соотношению
будет соответствовать матричное
соотношение:
![]() ,
,
или
![]() ,
,
(перенос правой
части налево:
![]() или
или
![]() ).
).
В результате мы получили следующую систему однородных уравнений:
![]() (1)
(1)
Данная система уравнений имеет неизвестных: среди них - неизвестных и число . Следовательно, для нахождения решения этой системы уравнений, необходимо еще одно уравнение, чтобы число неизвестных сравнялось с числом уравнений!
Мы знаем, что
однородная система уравнений имеет
нетривиальное решение
,
если
![]() меньше
.
Это условие можно записать в виде условия
на определитель матрицы
меньше
.
Это условие можно записать в виде условия
на определитель матрицы
![]() :
:
![]()
![]()
Мы получили уравнение степени относительно . Это уравнение называется характеристическим или вековым уравнением. Вот мы и получили недостающее -ое уравнение.
Это уравнение
имеет, по крайней мере, один корень
![]() .
Подставив в систему (1) вместо
корень
,
мы получим однородную систему уравнений,
определитель которой равен нулю, и
имеющую, следовательно, ненулевое
решение:
.
Подставив в систему (1) вместо
корень
,
мы получим однородную систему уравнений,
определитель которой равен нулю, и
имеющую, следовательно, ненулевое
решение:
![]() .
Тогда вектор
.
Тогда вектор
![]() будет собственным вектором, а
собственным значением линейного
оператора
,
так как
будет собственным вектором, а
собственным значением линейного
оператора
,
так как
![]()
Теорема доказана.
Характеристический
полином
![]() .
Дадим следующее определение:
.
Дадим следующее определение:
![]() .
Очевидно, что
.
Очевидно, что
![]() .
.
Спектр линейного оператора. Преобразование матрицы линейного оператора. Подобные матрицы.
Следствие теоремы.
Согласно основной теореме алгебры,
всякое уравнение
-ой степени имеет ровно
корней. Следовательно, характеристическое
уравнение
имеет
корней
![]() .
.
Определение. Множество собственных значений линейного оператора называется спектром линейного оператора.
Спектр линейного оператора не зависит от выбора базиса. Ниже мы докажем это свойство.
Рассмотрим в линейном пространстве некоторый линейный оператор .
Выберем в два базиса:
В базисе линейному оператору соответствует матрица : .
В базисе
оператору
будет
соответствовать некоторая матрица
![]() :
:
![]() .
.
Итак
![]()
ТЕОРЕМА.
Матрицы
и
связаны соотношением
![]() ,
где
,
где
![]() -
матрица перехода от базиса
к базису
-
матрица перехода от базиса
к базису
![]() .
.
Доказательство.
Итак,
![]() или
или
![]() .
.
Рассмотрим следующее выражение:
![]()
С другой стороны:
![]() Сравнивая
эти два соотношения, получаем
Сравнивая
эти два соотношения, получаем
![]()
В матричном виде это равенство имеет следующий вид:
![]() или
или
![]()
Теорема доказана.
Определение.
Матрицы
и
называются подобными,
если существует невырожденная матрица
![]() и
выполняется
и
выполняется
![]() .
.
