1. Равноправие строк и столбцов: .

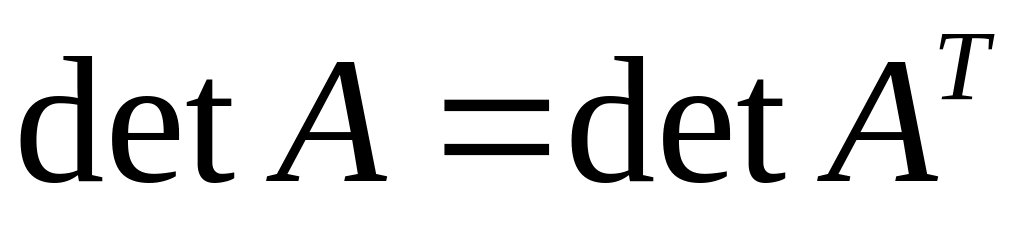2. Свойство антисимметрии: при перестановке любых 2-х строк (любых столбцов) изменяется знак определителя.

3. Основное свойство:

4. Линейное свойство:

ТЕОРЕМА 2. Для квадратных матриц выполняется соотношение:

Доказательство. Пусть матрицы и порядка . Рассмотрим две матрицы и порядка , составленные из матриц и :

и

Вычислим при разложении по первым строкам

.

Вычислим при разложении по последним строкам

Используя метод элементарных преобразований, докажите, что .

Доказательство провести самостоятельно.

Замечание: Если матрицы и прямоугольные, но их произведение является квадратной матрицей, то вычисляется по формуле Бине.

Обратная матрица. Рассмотрим квадратную матрицу порядка .

ОПРЕДЕЛЕНИЕ: Матрица называется правой обратной для матрицы если , а матрица называется левой обратной для матрицы если .

Докажем, что правая и левая обратные равны между собой :

Свойства операции сложения:

• Умножение матрицы на число:

, где

Свойства операции умножения:

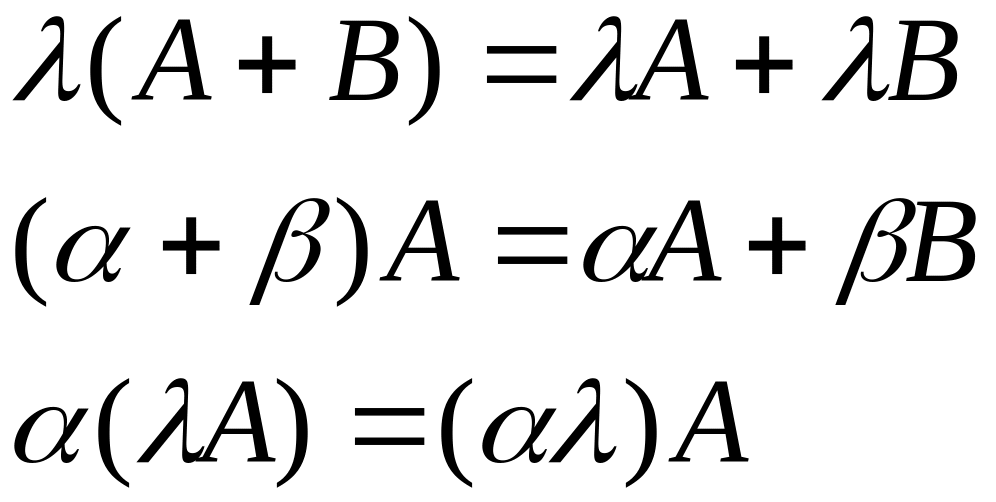
• Произведение двух матриц

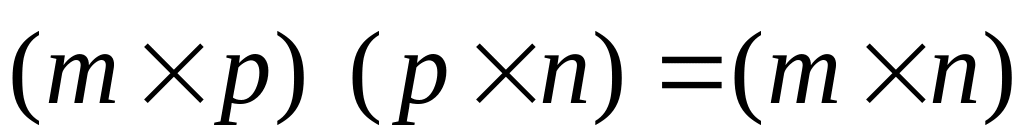
, где элементы матрицы

Это правило «читается» следующим образом: элемент равен сумме произведений элементов ой строки первой матрицы умноженных на элементы го столбца второй матрицы.

Очевидно, что произведение матриц не коммутативно. В общем случае . Если , то говорят, что матрицы и коммутативны. Произведение матриц ассоциативно и дистрибутивно.

Свойства операции произведения:

Для квадратных матриц можно определить следующие операции произведения:

- произведение Ли, или коммутатор.

- произведение Иордана, антикоммутатор

• Транспонирование.

Рассмотрим матрицу . Выполним над строками матрицы следующее действие – строки матрицы запишем как столбцы некоторой матрицы , которая называется транспонированной, по отношению к матрице :

, .

Операция над матрицей, подобная данной, называется транспонированием. Операцию транспонирования модно применять к матрицам любого порядка.

Свойства операции транспонирования:

Для квадратных матриц выполняется ряд свойств. Если матрица совпадает со своей транспонированной, , то такая матрица называется симметричной. Элементы симметричной матрицы, симметрично расположенные относительно главной диагонали, равны между собой.

Если матрица противоположна своей транспонированной, , то такая матрица называется антисимметричной (кососимметричной). Элементы антисимметричной матрицы, симметрично расположенные относительно главной диагонали, противоположны, а элементы главной диагонали равны нулю.

Задача 1. Докажите свойство .

Задача 2. Докажите, что всякую квадратную матрицу можно представить в виде суммы симметричной и антисимметричной матрицы.

Задача 3. Докажите, что всякую функцию одного переменного можно представить в виде суммы четной и нечетной функции.

• След матрицы.

Определение. Сумма диагональных элементов квадратной матрицы называется следом матрицы:

Свойства следа произведения матриц:

• Прямая сумма матриц.

Рассмотрим матрицы и порядка . Определим прямую сумму этих матриц. Прямая сумма обозначается символом окружность со знаком сложения.

, где матрица имеет следующий вид

.

Следовательно, матрица будет иметь порядок .

Очевидно, т.е., результат вычисления прямой суммы зависит от порядка следования матриц и при сложении. Таким образом, при операции прямой суммы матрицы не коммутативна, т.е. не перестановочны.

Следует отметить, что матрица имеет блочную структуру, или как говорят, имеет блочно диагональный вид. По главной диагонали расположены матрицы и , а по второстепенной (не главной) – нулевые матрицы .