
- •Лекция 1
- •Мир не линеен и поэтому сложен.
- •Основное свойство:
- •Линейное свойство:
- •Лекция 3
- •Лекция 4
- •Лекция 6 лекция 7
- •Лекция 8
- •Лекция 9
- •Лекция 10 лекция 11
- •Свойства подобных матриц.
- •Лекция 12
- •Лекция 13 лекция 14
- •Лекция 15
- •Лекция 16
- •Программа по линейной алгебре для студентов 1 курса физического факультета
- •I. Матрицы и определители
- •II. Линейные пространства
- •III. Системы линейных уравнений
- •IV. Евклидовы и унитарные пространства.
- •V. Линейные операторы в конечномерном пространстве.
- •VI. Билинейные и квадратичные формы. Функции от матриц.
- •Д.К.Фаддеев ”Лекции по алгебре” 2005г.
- •1. Проскуряков м.В.: - Сборник задач по линейной алгебре
- •2.Фаддеев д.К., Соминский и.С.: - Задачи по высшей алгебре
Лекция 3
Обратная матрица. Линейная зависимость строк матрицы (столбцов). Ранг матрицы и его свойства.
-
“Утверждать, что социальный прогресс производит нравственность, все равно, что утверждать, что постройка печей производит тепло”
Л.Н.Толстой
Обратная матрица. Рассмотрим квадратную матрицу порядка .
ОПРЕДЕЛЕНИЕ:
Матрица
называется правой
обратной
для матрицы
,
если произведение
![]() ,
а матрица
называется левой
обратной
для
если
,
а матрица
называется левой
обратной
для
если
![]() .
.
Докажем что, левая обратная матрица равна правой обратной, т.е. :
![]()
Введем обозначение
обратной матрицы:
![]() :
:
![]() .
.
Свойство:
![]() .
.
Доказательство:
Очевидно, что
![]() .
Выполним
следующие действия
.
Выполним
следующие действия
![]() Сравнив,
мы получим доказательство этого свойства.
Сравнив,
мы получим доказательство этого свойства.
Вопрос: А существует ли обратная матрица?
Ответ: Существует, причем только для квадратных матриц, у которых определитель не равен нулю, см. ниже Теорему 3.
ТЕОРЕМА 3.
Для того, чтобы у матрицы
существовала обратная необходимо и
достаточно, чтобы
![]()
Доказательство. Необходимость.
Пусть обратная
матрица
![]() существует. Тогда выполняется
.
существует. Тогда выполняется
.
Согласно Теореме
2., имеем
![]() .
.
Следовательно
![]() ,
причем
,
причем
![]() .
.
Достаточность.
Пусть
Построим матрицу
, используя для этого алгебраические
дополнения
![]() матрицы
и условие
:
матрицы
и условие
:
![]()
Используя
основное свойство определителей,
вычислим
![]()
![]()
![]()
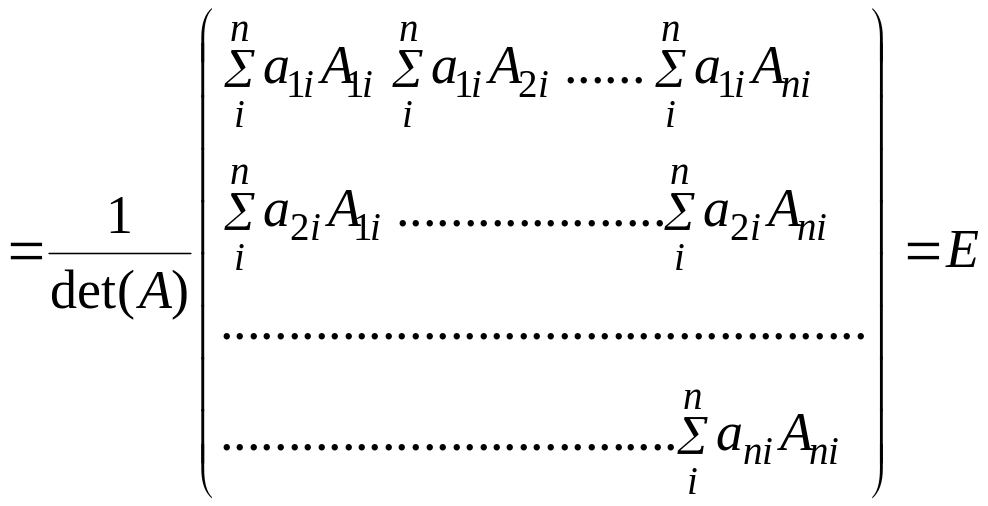
Теорема доказана.
Линейная зависимость строк матрицы (столбцов).
Рассмотрим строки
![]() некоторой прямоугольной матрицы
порядка
некоторой прямоугольной матрицы
порядка
![]() :
:
![]()
![]()
…………………………………
![]()
Матрицу можно записать в виде столбца, каждый элемент столбца является строкой:
![]()
Из некоторого набора строк матрицы составим выражение вида
![]() ,
(1)
,
(1)
где
![]() произвольный
набор вещественных чисел. Дадим следующее
определение.
произвольный
набор вещественных чисел. Дадим следующее
определение.
ОПРЕДЕЛЕНИЕ:
Выражение
вида
называется
линейной
комбинацией
строк
![]() ,
а вещественные числа
,
а вещественные числа
![]() -
коэффициентами
линейной комбинации.
-
коэффициентами
линейной комбинации.
Если все коэффициенты линейной комбинации равны нулю, то такую линейную комбинацию называют тривиальной, если нет – то нетривиальной.
Набор строк будем называть системой строк.
Теперь мы можем сформулировать важнейшее в линейной алгебре определение линейной зависимости системы строк.
ОПРЕДЕЛЕНИЕ: Система строк называется линейно зависимой, если линейная комбинация этих строк, равная нулевой строке,
![]()
является
нетривиальной,
т.е. среди чисел
найдутся
не равные нулю, и называется
линейно-независимой
в том
случае, когда
их линейная комбинация является
тривиальной,
т.е. когда все коэффициенты
![]() .
.
Поясним это определение.
Во-первых. Система строк (или просто строки) линейно-независимы, если равенство
![]()
выполняется, только тогда, когда все числа .
Во-вторых. Система строк линейно-зависима, если равенство
выполняется, когда среди найдутся не равные нулю.
В такой интерпретации понятия линейной зависимости и линейной независимости мы и будем использовать в дальнейшем.
ТЕОРЕМА 4. Для того, чтобы система строк была линейно зависимой необходимо и достаточно, чтобы одна из строк являлась линейной комбинацией остальных строк.
Доказательство.
Необходимость.
Пусть строки
![]() линейно
зависимы.
Тогда, согласно определению, нулевая
линейная комбинация этих строк
линейно
зависимы.
Тогда, согласно определению, нулевая
линейная комбинация этих строк
![]()
является нетривиальной
и пусть
![]() (так можно считать). Преобразуя это
выражение, получим
(так можно считать). Преобразуя это
выражение, получим
![]() .
.
Следовательно,
строка
![]() является линейной комбинацией остальных.
является линейной комбинацией остальных.
Достаточность. Пусть строка является линейной комбинацией остальных строк
![]() .
(2)
.
(2)
Тогда, преобразуя (2), получаем нулевую линейную комбинацию
![]()
Так как
![]() ,
то согласно определению это означает,
что система строк
линейно
зависима.
,
то согласно определению это означает,
что система строк
линейно
зависима.
Доказательство завершено.
Ранг матрицы.
Одной из важнейших количественных характеристик матрицы является ее ранг. Ранг матрицы является натуральным числом. Определим это число.
Дадим два определения.
ОПРЕДЕЛЕНИЕ 1. Ранг матрицы равен числу линейно независимых строк матрицы (столбцов).
ОПРЕДЕЛЕНИЕ
2. Ранг матрицы
равен порядку минора, не равного нулю,
причем все миноры
![]() порядка равны нулю.
порядка равны нулю.
Итак, в матрице
существует минор
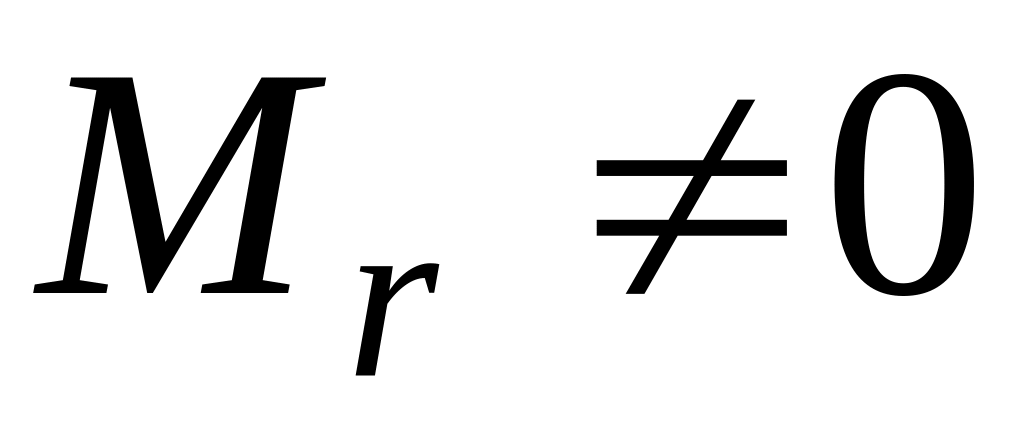 ,
,все миноры
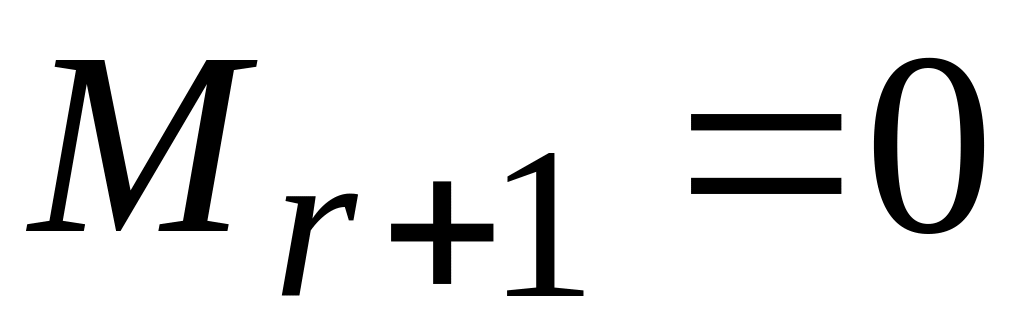 ,
,
где
![]() минор
без черты порядка
минор
без черты порядка
![]() .
.
Обозначение
ранга
матрицы:
![]()
По определению
ранг нулевой
матрицы
равен нулю,
![]() .
.
Пусть матрица порядка , тогда ранг матрицы удовлетворяет следующему неравенству
![]() .
.
ОПРЕДЕЛЕНИЕ.
Пусть
.
Тогда тот минор порядка
,
который не равен нулю
![]() ,
называется базисным
минором.
Строки и столбцы базисного минора
называются базисными
строками и столбцами.
,
называется базисным
минором.
Строки и столбцы базисного минора
называются базисными
строками и столбцами.
Существуют два метода вычисления ранга матрицы:
Метод окаймляющих миноров;
Метод элементарных преобразований;
Ранг произведения
квадратных матриц порядка
:
![]()
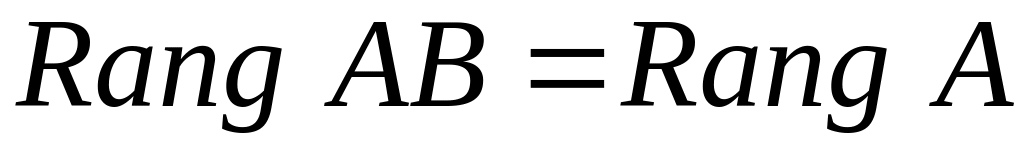 ,
если
,
если
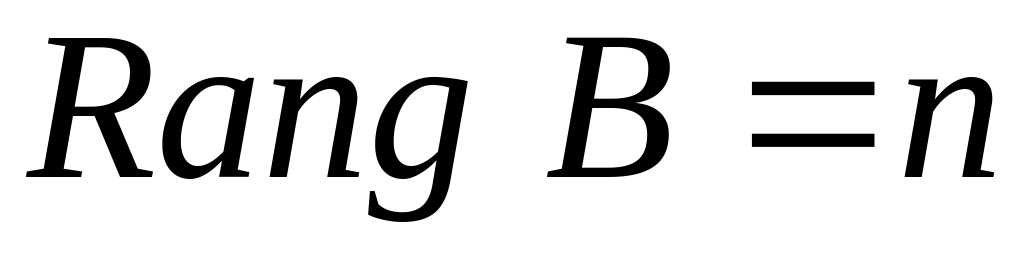 .
.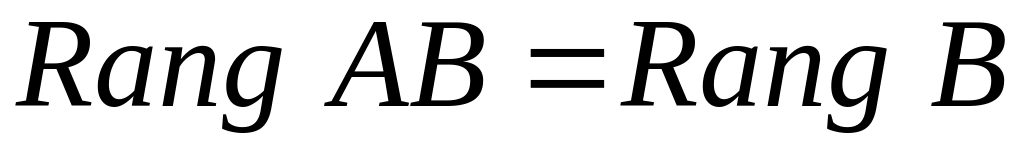 ,
если
,
если
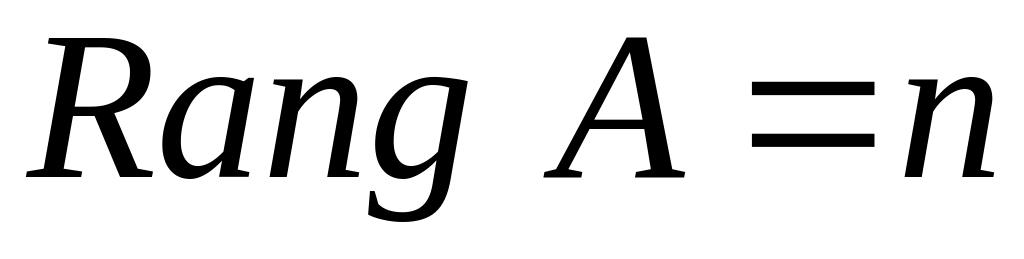 .
.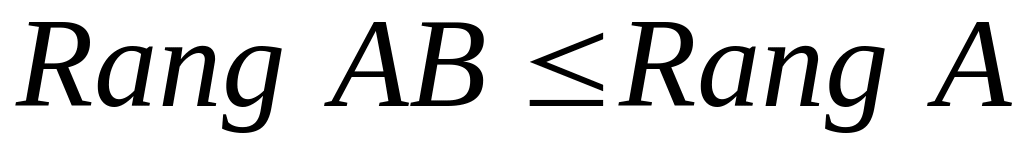 (
(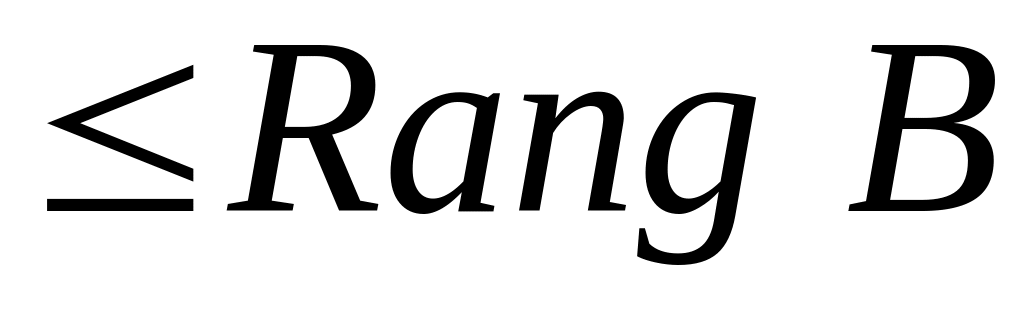 ).
). .
.
ТЕОРЕМА 5. О базисном миноре. Базисные строки и столбцы линейно независимы. Все остальные строки (столбцы) матрицы являются линейными комбинациями базисных строк (столбцов).
Доказательство.
1). Рассмотрим базисный минор (напомним, базисный минор не равен нулю). Предположим, что базисные строки линейно зависимы. Тогда по Теореме 4. одна из строк является линейной комбинацией остальных строк. Вычитая линейную комбинацию из этой строки, мы получим нулевую строку. В результате базисный минор будет равен нулю, а это противоречит условию, что базисный минор не равен нулю. Следовательно, базисные строки линейно независимы.
2). Пусть
и
- базисный минор. Допустим, что базисный
минор
расположен в левом верхнем углу
![]() .
Рассмотрим минор
.
Рассмотрим минор
![]() .
Этот минор равен нулю при всех значениях
.
Этот минор равен нулю при всех значениях
![]() и
и
![]() .
Разложим минор по столбцу
.
Разложим минор по столбцу
![]() ,
,
Очевидно
![]() .
Следовательно
.
Следовательно
![]() ,
,
или
![]()
В итоге строка
![]() является линейной комбинацией базисных
строк.
является линейной комбинацией базисных
строк.
