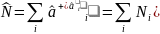Лекция №1
Вторичное квантование
Необходим для описания систем с переменным числом частиц.
Пусть Ψ1 (ξ), Ψ2 (ξ), … – некоторая полная ортонормированная система волновых функций стационарных состояний одной частицы (ξ – набор координат и проекций спина)
Обычно это плоские волны – волновая функция свободной частицы с определенными значениями импульса и проекций спина.
Обычно для сведения спектра состояний к дискретному, рассматривают движение частиц в большом объеме V.
В системе свободных частиц импульсы частиц сохраняются по отдельности.
Тем самым сохраняются и числа заполнения состояний – числа N1, N2, …, указывающие, сколько частиц находится в каждом из состояний Ψ1, Ψ2, …
В системе взаимодействующих частиц импульсы каждой из них уже не сохраняются, а потому не сохраняются и числа заполнения.
Для такой системы можно говорить лишь о распределении вероятностей различных значений чисел заполнения.
Поставим себе целью построить математический аппарат, в котором именно числа заполнения (а не координаты и проекции спина) играют роль независимых переменных.
В таком аппарате состояние системы описывается «волновой функцией в пространстве чисел заполнения», которую мы обозначим как Ф(N1, N2, …,t).
Обычная координатная функция обозначается Ψ(ξ1, ξ2,…,t)
Тогда и операторы различных физических величин должны формулироваться в терминах их воздействия на функции чисел заполнения.
Теперь рассмотрим вопрос с другой стороны. Пусть имеется система бозонов.
Рассмотрим преобразование уравнения Шредингера в представлении чисел заполнения
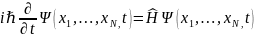
Пусть имеем одночастичный гамильтониан

Волновую функцию можно представить в виде суперпозиции волновых функций свободного состояния
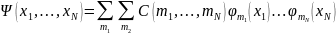
Где
mi
– совокупность квантовых чисел
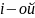 частицы, характеризующих состояние
одной частицы и кратко называемых
уровнем
(три компоненты импульса и спина). Тогда
матричные элементы есть
частицы, характеризующих состояние
одной частицы и кратко называемых
уровнем
(три компоненты импульса и спина). Тогда
матричные элементы есть
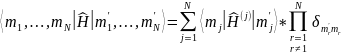
Уравнение
Шредингера преобразуется стандартным
образом и даст уравнение для определения
коэффициентов
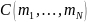
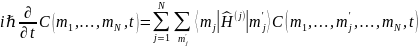
Интерпретация
правой части хорошо известна. Гамильтониан
определяет переходы частицы j
с уровня
 на уровень
на уровень
 ,
а эволюция во времени определяется
суммой всевозможных переходов этого
типа. Амплитуда вероятности каждого
перехода представляет собой матричный
элемент гамильтониана.
,
а эволюция во времени определяется
суммой всевозможных переходов этого
типа. Амплитуда вероятности каждого
перехода представляет собой матричный
элемент гамильтониана.
Теперь выразим эту же мысль в представлении чисел заполнения.
До
перехода имелось
 частиц на уровне
и
частиц на уровне
и
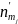 частиц на уровне
.
частиц на уровне
.
После
перехода число частиц на уровне
стало равным
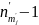 ,
а на уровне
,
а на уровне
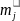 стало равным
стало равным
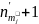 . Этот процесс можно изобразить как
уничтожение частицы на уровне
и рождение частицы на уровне
.
. Этот процесс можно изобразить как
уничтожение частицы на уровне
и рождение частицы на уровне
.
Теперь рассмотрим это описание на рис.
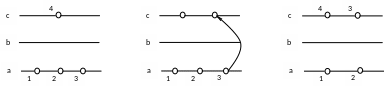
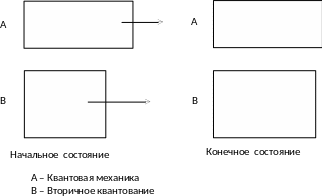
Оператор
уничтожения
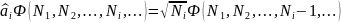
Или можно представить в виде матрицы, единственный отличный от нуля элемент которой есть

Сопряженный
оператор
 i+
изображается матрицей с единственным
элементом
i+
изображается матрицей с единственным
элементом
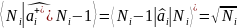
Это
означает, что при воздействии на функцию
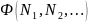 он увеличивает число
он увеличивает число
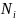 на 1.
на 1.
Оператор
рождения
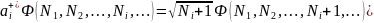
Вычислим произведения операторов
i+ i – такой оператор может лишь умножить волновую функцию на константу, оставляя все переменные N1, … неизменными.
Можно
показать, что
i+
i=
и
i+
i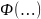 =
=
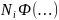
Аналогичным
образом найдем
i
i+=
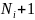
Разность этих элементов дает правило коммутации i i+ - i+ i = 1
Операторы
же с различными индексами
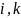 ,
действующие на различные переменные,
коммутативны
,
действующие на различные переменные,
коммутативны
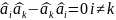
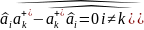
Аналогично можно получить обобщение и на симметричные по всем частицам операторы любого другого вида. Таким образом, гамильтониан системы взаимодействующих частиц есть
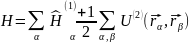
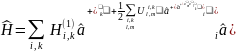
Одночастичный гамильтониан есть
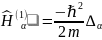
Для системы невзаимодействующих частиц имеем
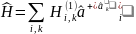
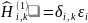
Поэтому
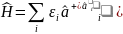
Так
как
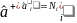 , то получим очевидный результат
, то получим очевидный результат
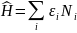
Теперь
представим формализм вторичного
квантования в координатном представлении.
Введем в рассмотрение так называемые
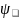 – операторы.
– операторы.
(
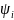 – волновые ортонормированные функции)
– волновые ортонормированные функции)
Вторично квантованные операторы
Переменные
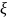 рассматриваются как параметры
рассматриваются как параметры
Аналогия:
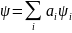 – разложение произвольной функции по
базису – отсюда название «вторичное
квантование»
– разложение произвольной функции по
базису – отсюда название «вторичное
квантование»
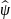 – уменьшает
число частиц на единицу в точке
– уменьшает
число частиц на единицу в точке
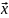
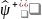 – увеличивает
число частиц на единицу в точке
– увеличивает
число частиц на единицу в точке
Гамильтониан перепишется в виде:

Далее:
Оператор
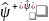 – оператор плотности числа частиц, так
как
– оператор плотности числа частиц, так
как
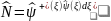
 – оператор
полного числа частиц.
– оператор
полного числа частиц.
Проверка:
подставив в
определение ,
получим
,
получим