
- •Лекция 1
- •Мир не линеен и поэтому сложен.
- •Основное свойство:
- •Линейное свойство:
- •Лекция 3
- •Лекция 4
- •Лекция 6 лекция 7
- •Лекция 8
- •Лекция 9
- •Лекция 10 лекция 11
- •Свойства подобных матриц.
- •Лекция 12
- •Лекция 13 лекция 14
- •Лекция 15
- •Лекция 16
- •Программа по линейной алгебре для студентов 1 курса физического факультета
- •I. Матрицы и определители
- •II. Линейные пространства
- •III. Системы линейных уравнений
- •IV. Евклидовы и унитарные пространства.
- •V. Линейные операторы в конечномерном пространстве.
- •VI. Билинейные и квадратичные формы. Функции от матриц.
- •Д.К.Фаддеев ”Лекции по алгебре” 2005г.
- •1. Проскуряков м.В.: - Сборник задач по линейной алгебре
- •2.Фаддеев д.К., Соминский и.С.: - Задачи по высшей алгебре
Лекция 4
Линейное (векторное) пространство. Примеры линейных пространств. Линейная зависимость. Теорема о линейной зависимости. Базис и размерность линейного пространства. Примеры базисов.
-
«Часто приходится встречаться с объектами, над которыми производятся операции сложения и умножения на числа»
Линейное (векторное) пространство.
Рассмотрим
некоторое множество
![]() ,
состоящее из элементов
,
состоящее из элементов
![]() произвольной природы. Пусть в
определены операции сложения двух
элементов
произвольной природы. Пусть в
определены операции сложения двух
элементов
![]() и умножения элемента
и умножения элемента
![]() на число α,
α
.
на число α,
α
.
Символическая форма записи этих операций:
Операция сложения
![]() ,
,
Операция умножения
![]() .
.
Символом
![]() обозначается декартово произведение
множества
на множество
,
а символом
обозначается декартово произведение
множества
на множество
,
а символом
![]() декартово произведение множества
на множество
,
где
-
множество вещественных чисел.
декартово произведение множества
на множество
,
где
-
множество вещественных чисел.
Примерами операций сложения и умножения являются хорошо знакомые операции сложения и умножения обычных вещественных чисел, операции сложения трехмерных векторов и умножения вектора на число, операции сложения матриц и умножения матрицы на число, сложения функций и умножения функции на число и т.п.
Эти операции можно задать различными способами, лишь бы они обладали определенным набором свойств или аксиом, которые мы определим ниже.
Дадим строгое определение линейного пространства.
ОПРЕДЕЛЕНИЕ. Множество называется линейным пространством, а его элементы векторами, если в нем определены следующие две операции:
а) операция
сложения
векторов (правило сложения или закон
сложения), по которому любым двум векторам
и
![]() из
сопоставляется некоторый вектор
из
сопоставляется некоторый вектор
![]() ,
называемый их суммой и обозначаемый
,
называемый их суммой и обозначаемый
![]()
б) операция
умножения вектора на число,
по которому каждому вектору
из
и числу α
сопоставляется
некоторый вектор
![]() из
,
называемый произведением вектора на
число и обозначаемый
из
,
называемый произведением вектора на
число и обозначаемый
![]() .
.
Для этих операций должны быть выполнены следующие 8 аксиом:
|
8.
|
Вектор в аксиоме 3 называется нулевым вектором.
Вектор в аксиоме 4 называется вектором противоположным к вектору .
Если в пункте б) определения мы рассматриваем вещественные числа, то в этом случае называется вещественным линейным пространством. Если же рассматриваем комплексные числа, то линейное пространство называется комплексным (или унитарным) линейным пространством.
Линейное пространство является также и группой (см. Теория групп).
Рассмотри различные числовые множества – множество вещественных чисел, комплексных чисел, множество строк из вещественных (или комплексных) чисел, множество матриц, множество полиномов, множество функций и т.д. В каждом из этих множеств можно ввести операции сложения и умножения на числа. В результате мы получим примеры линейных пространств.
Примеры линейных пространств:
 .
Множество вещественных чисел
.
Множество вещественных чисел
 является вещественным линейным
пространством по отношении к обычным
операциям сложения и умножения
вещественных чисел. Проверьте выполнимость
аксиом.
является вещественным линейным
пространством по отношении к обычным
операциям сложения и умножения
вещественных чисел. Проверьте выполнимость
аксиом.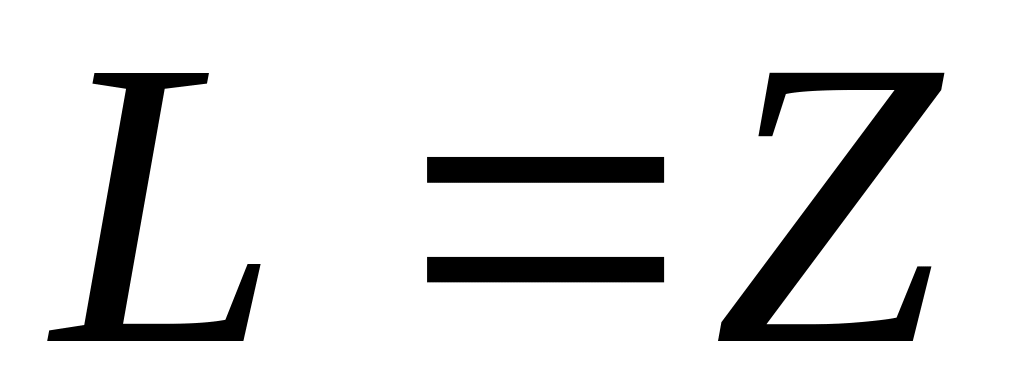 .
Множество комплексных чисел
.
Множество комплексных чисел
 является комплексным линейным
пространством по отношению к обычным
операциям сложения и умножения
комплексных чисел. Проверьте выполнимость
аксиом.
является комплексным линейным
пространством по отношению к обычным
операциям сложения и умножения
комплексных чисел. Проверьте выполнимость
аксиом.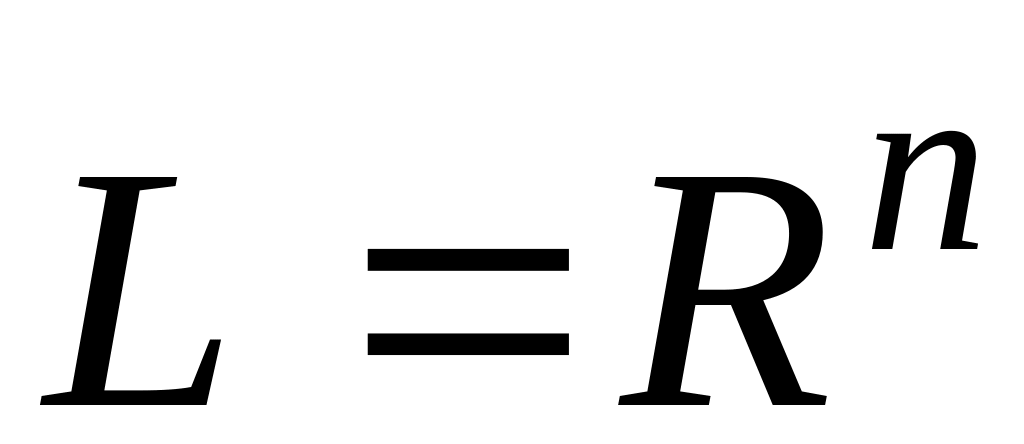 .
Множество строк
.
Множество строк
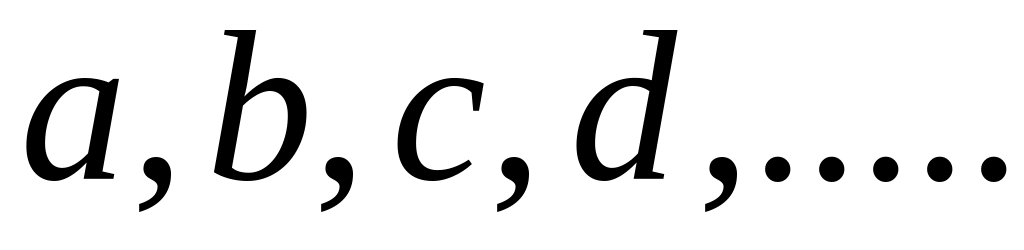 длиной
вида
длиной
вида
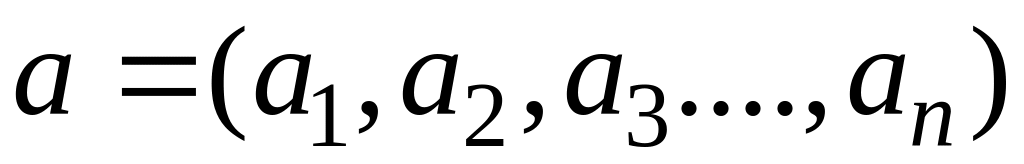 ,
где
,
где
 - вещественные числа является вещественным
линейным пространством. Это пространство
известно, как
-
мерное координатное пространство
- вещественные числа является вещественным
линейным пространством. Это пространство
известно, как
-
мерное координатное пространство
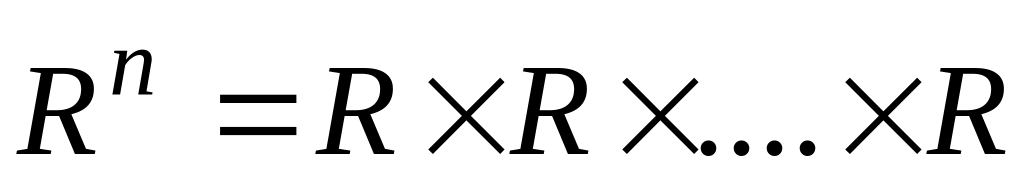 (см. математический
анализ, теоретическая физика).
(см. математический
анализ, теоретическая физика).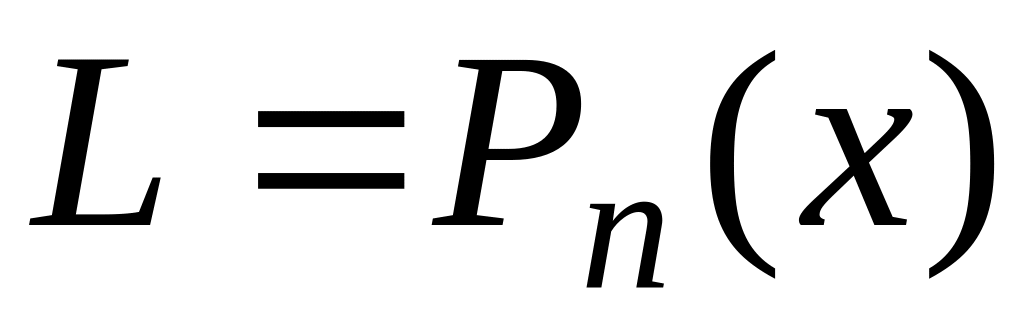 .
Множество
.
Множество
 образуют полиномы от одной переменной
,
степень которых не выше заданного
натурального числа
,
вида
образуют полиномы от одной переменной
,
степень которых не выше заданного
натурального числа
,
вида
![]() .
.
Это множество является вещественным линейным пространством. Действительно, сумма двух полиномов степени есть полином степени не выше , произведение полинома на вещественное число также является полиномом и принадлежит этому же множеству полиномов. Таким образом, всякий полином является вектором линейного пространства.
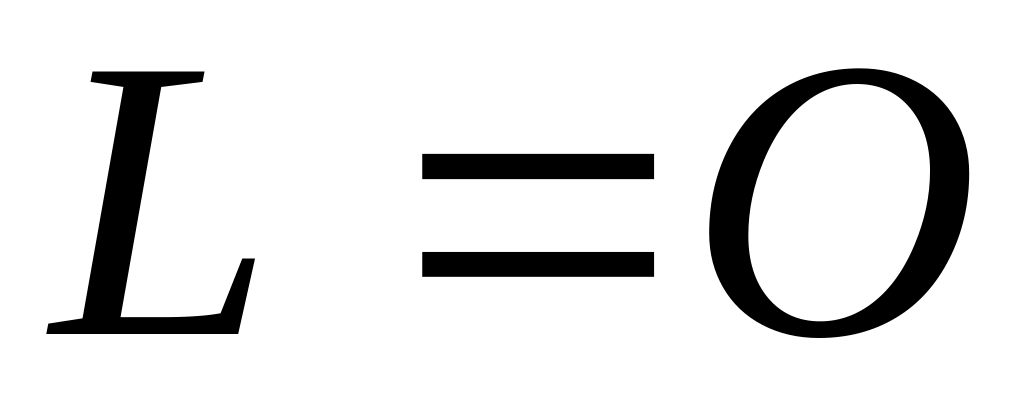 .
Существует линейное пространство
,
состоящее из одного вектора. Такое
пространство называется нулевым.
Единственный вектор этого пространства,
по необходимости, оказывается нулевым
вектором и самому себе противоположным.
.
Существует линейное пространство
,
состоящее из одного вектора. Такое
пространство называется нулевым.
Единственный вектор этого пространства,
по необходимости, оказывается нулевым
вектором и самому себе противоположным.
 .
Множество
.
Множество
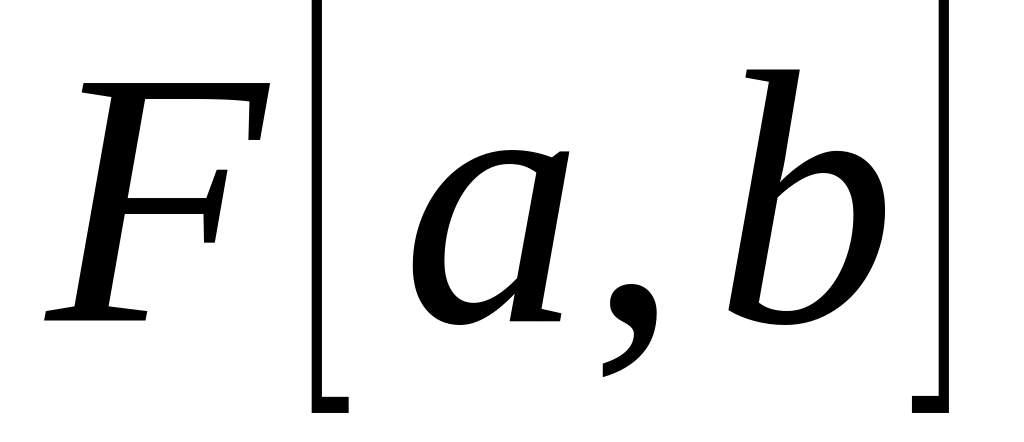 состоит из функций
состоит из функций
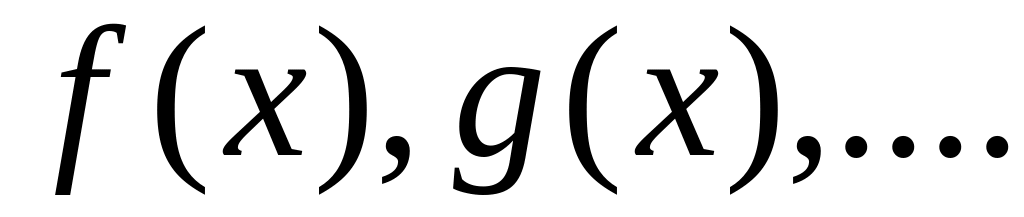 от одной независимой переменной
,
определенных и непрерывных на отрезке
от одной независимой переменной
,
определенных и непрерывных на отрезке
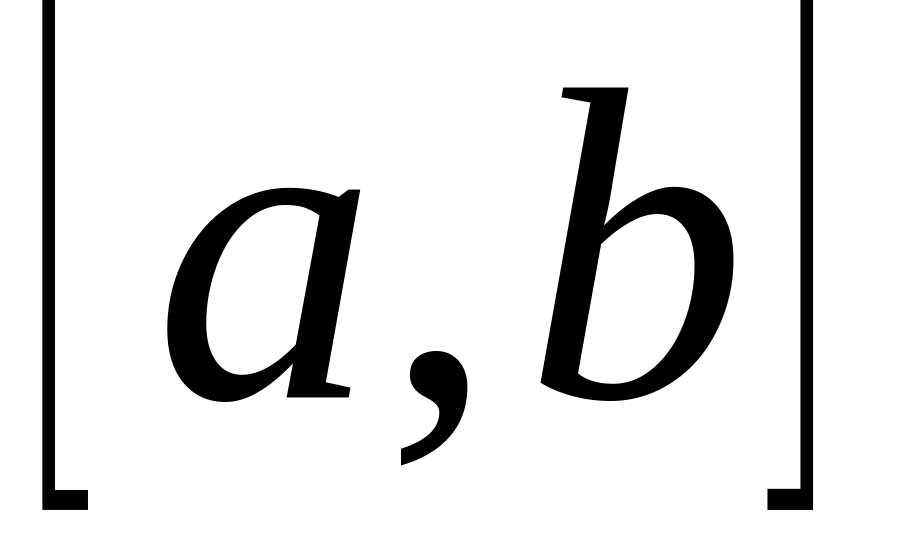 .
Оно образует линейное пространство.
Любым двум функциям
.
Оно образует линейное пространство.
Любым двум функциям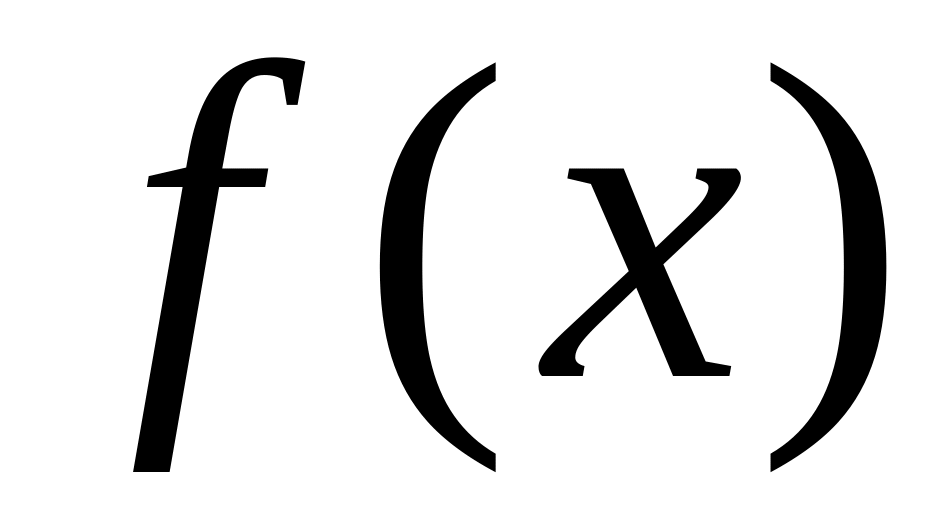 и
и
 и числу
и числу
 можно сопоставить их сумму и произведение
в обычном смысле слова
можно сопоставить их сумму и произведение
в обычном смысле слова
![]() ,
,
![]() .
.
Роль нулевого вектора играет нулевая функция. Можно без труда проверить, что все аксиомы выполнены.
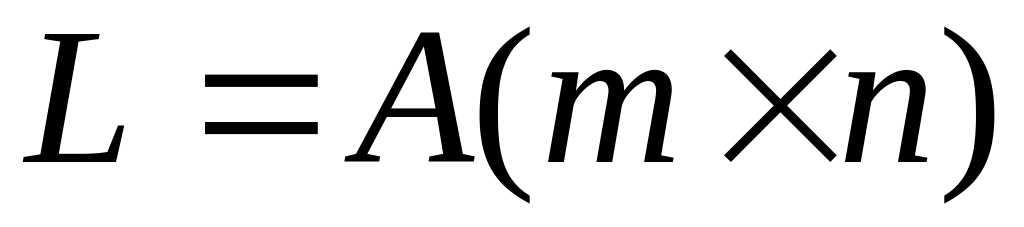 .
Множество
.
Множество
 матриц порядка
матриц порядка
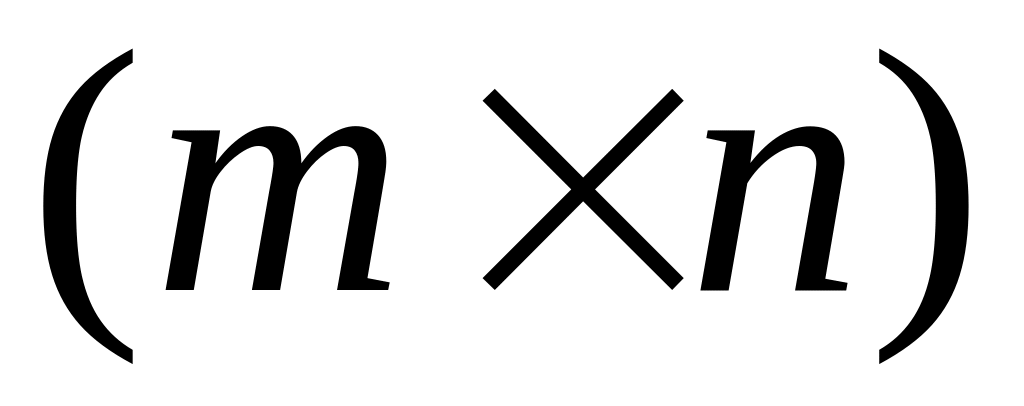 является линейным пространством.
Действительно, сумма двух матриц
и
равна некоторой третьей матрице
,
произведение матрицы на число есть
также некоторая матрица
:
является линейным пространством.
Действительно, сумма двух матриц
и
равна некоторой третьей матрице
,
произведение матрицы на число есть
также некоторая матрица
:
![]()
Линейная зависимость. Теорема о линейной зависимости.
Пусть – линейное пространство.
Рассмотрим в
некоторую конечную систему векторов
![]() .
.
Введем следующие понятия. Выражение:
![]()
называется линейной комбинацией этой системы векторов.
При этом:
Линейная комбинация называется тривиальной, если мы рассматриваем случай, когда коэффициенты равны нулю:
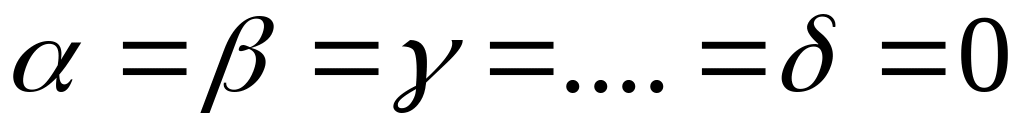 .
.Линейная комбинация называется нетривиальной, если мы рассматриваем случай, когда среди коэффициентов есть ненулевые, т.е. хотя бы один из коэффициентов не равен нулю.
При образовании линейной комбинации мы вправе выбирать произвольные наборы значений коэффициентов. Если мы выбираем набор нулевых коэффициентов, то линейная комбинация векторов является, очевидно, тривиальной, для ненулевых коэффициентов – очевидно, нетривиальная. Третьего исхода здесь не дано.
Дадим определение линейной зависимости системы векторов, которое является в Линейной алгебре основным или, как говорят, фундаментальным понятием.
ОПРЕДЕЛЕНИЕ. Система векторов называется линейно зависимой, если равная нулевому вектору линейная комбинация этих векторов
![]() (1)
(1)
является
нетривиальной,
в противном
случае возможна только тривиальная
линейная комбинация,
т.е когда все коэффициенты
![]() и система векторов в этом случае
называется
линейно независимой.
и система векторов в этом случае
называется
линейно независимой.
Соотношение (1),
фактически, является уравнением, в
котором неизвестными величинами являются
коэффициенты
![]() .
Отметим, что уравнение (1) всегда имеет
решение.
.
Отметим, что уравнение (1) всегда имеет
решение.
Свойство 1. Каждая подсистема линейно независимой системы векторов является, сама, линейно независимой.
Свойство 2. Если в систему векторов входит нулевой вектор, то она является линейно зависимой.
ТЕОРЕМА 6. Для того, чтобы система векторов была линейно зависимой, необходимо и достаточно, чтобы один из векторов линейно выражался через остальные (аналог Теоремы 4).
Доказательство.
Необходимость. Пусть система векторов является линейно зависимой. Тогда нулевая линейная комбинация этих векторов
является
нетривиальной, т.е. среди коэффициентов
есть не равные нулю. Пусть
![]() ,
тогда при делении на
мы получаем
,
тогда при делении на
мы получаем
![]() .
.
Следовательно, вектор линейно выражается через остальные, или является линейной комбинацией остальных векторов.
Достаточность. Пусть вектор является линейной комбинацией остальных векторов
![]() .
.
Перенесем вектор в правую часть уравнения
![]()
В
результате мы получили нетривиальную
линейную комбинацию, так как при векторе
коэффициент
![]() .
Следовательно, система векторов является
линейно зависимой.
.
Следовательно, система векторов является
линейно зависимой.
Доказательство теоремы завершено.
Базис и размерность линейного пространства.
При рассмотрении свойств линейного пространства возникает очевидный вопрос о существовании максимальной линейно независимой системы векторов.
Рассмотрим следующий вопрос: сколько векторов может насчитывать максимальная линейно независимая система векторов данного линейного пространства. Если такая система векторов существует (а она существует), то она имеет особое значение.
Следующие основные понятия:
базис линейного пространства,
размерность линейного пространства,
координаты вектора.
Эти понятия будут играть важную роль в дальнейшем.
ОПРЕДЕЛЕНИЕ. Базисом линейного пространства называется такая система векторов, которая удовлетворяет следующим двум условиям:
а) это линейно независимая система векторов;
б) каждый вектор из является линейной комбинацией этой линейно независимой системы векторов.
ОПРЕДЕЛЕНИЕ. Линейное пространство , в котором существует базис из векторов называется -мерным, а число называется размерностью пространства.
Для указания размерности пространства используется символическая запись:
![]() ,
,
(![]() dimension
= размерность).
dimension
= размерность).
В дальнейшем векторы базиса -мерного линейного пространства мы будем обозначать следующим образом:
![]() - базис линейного
пространства
.
Фактически мы упорядочили векторы
базиса, присвоив каждому из них номер.
Это будет весьма полезно для дальнейшего.
- базис линейного
пространства
.
Фактически мы упорядочили векторы
базиса, присвоив каждому из них номер.
Это будет весьма полезно для дальнейшего.
Известно меткое философское высказывание: форма существенна, сущность оформлена.
Согласно пункту б) ОПРЕДЕЛЕНИЯ любой вектор линейного пространства, например, вектор , всегда является линейной комбинацией базисных векторов:
![]() (2)
(2)
Это выражение можно записать в компактной форме
![]() (3)
(3)
Числа
![]() являются
компонентами или координатами вектора
по базису.
являются
компонентами или координатами вектора
по базису.
Таким образом, мы приходим к следующему определению:
ОПРЕДЕЛЕНИЕ. Числа в (2) называются координатами вектора в базисе .
Координаты вектора можно записать либо в виде строки
![]() ,
,
либо в виде столбца
![]() .
.
Таким образом, координаты вектора можно записать в виде матрицы, состоящей из одной строки и - столбцов, или - строк и одного столбца.
Эти записи равноправны, так как мы уже знакомы с операцией транспонирования матриц. А именно, при транспонировании строки получается столбец и, наоборот, при транспонировании столбца получается строка.
Примеры базисов:
 .
Множество вещественных чисел
является вещественным линейным
пространством по отношении к обычным
операциям сложения и умножения
вещественных чисел.
.
Множество вещественных чисел
является вещественным линейным
пространством по отношении к обычным
операциям сложения и умножения
вещественных чисел.
Размерность этого
пространства
![]() ,
следовательно, базис состоит из одного
вектора (в данном случае числа). В
качестве базисного вектора можно выбрать
число 1:
,
следовательно, базис состоит из одного
вектора (в данном случае числа). В
качестве базисного вектора можно выбрать
число 1:
![]()
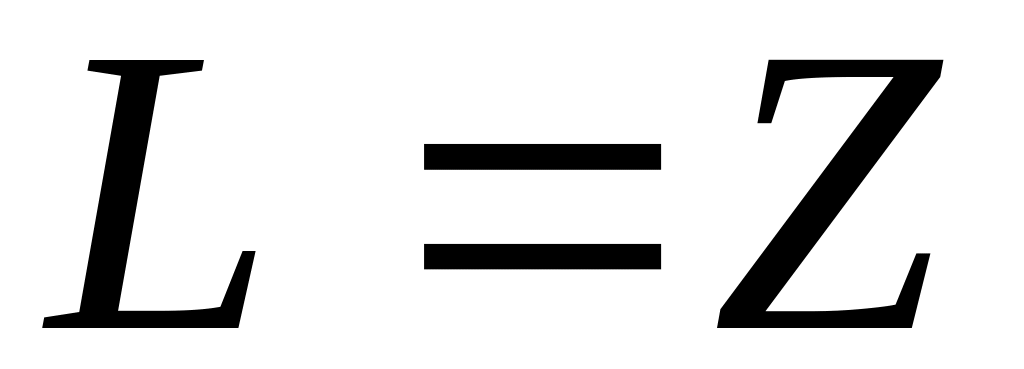 .
Множество комплексных чисел
является комплексным линейным
пространством по отношению к обычным
операциям сложения и умножения
комплексных чисел. Размерность этого
пространства
.
Множество комплексных чисел
является комплексным линейным
пространством по отношению к обычным
операциям сложения и умножения
комплексных чисел. Размерность этого
пространства
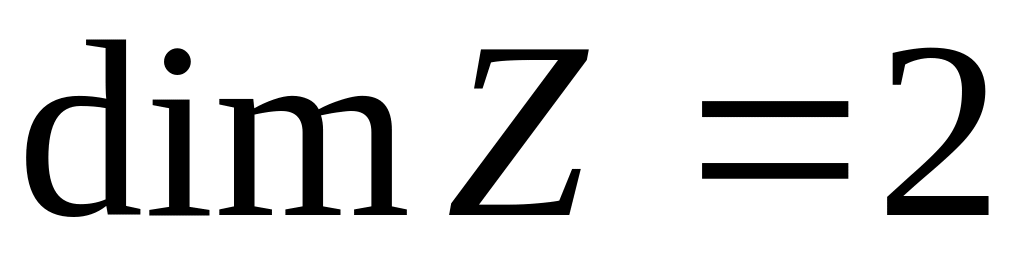 ,
следовательно, базис состоит из двух
векторов (в данном случае комплексных
чисел). В качестве базисных векторов
можно выбрать вещественное число 1 и
мнимую единицу
,
следовательно, базис состоит из двух
векторов (в данном случае комплексных
чисел). В качестве базисных векторов
можно выбрать вещественное число 1 и
мнимую единицу
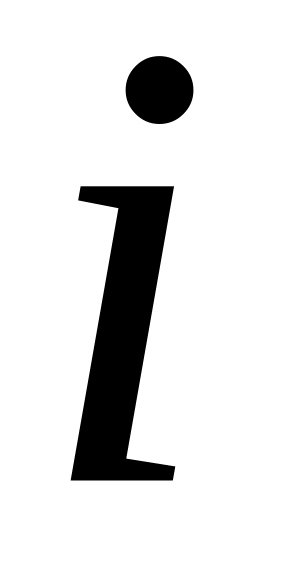 :
:
![]()
. Множество строк
 длиной
вида
,
где
- вещественные числа является вещественным
линейным пространством. Это пространство
известно, как
-
мерное координатное пространство.
длиной
вида
,
где
- вещественные числа является вещественным
линейным пространством. Это пространство
известно, как
-
мерное координатное пространство.
Размерность этого
пространства
![]() ,
следовательно, базис состоит из
векторов. В качестве базиса можно
выбрать следующие строки:
,
следовательно, базис состоит из
векторов. В качестве базиса можно
выбрать следующие строки:
![]()
![]()
![]()
……………………..
![]()
 .
Множество всех полиномов
.
Множество всех полиномов
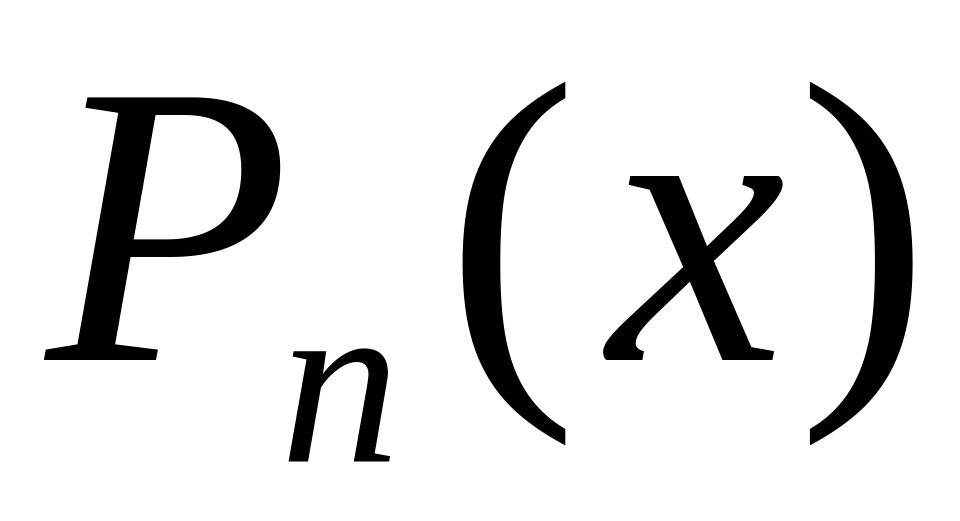 от
одной переменной, степень которых не
выше заданного числа
,
вида
от
одной переменной, степень которых не
выше заданного числа
,
вида
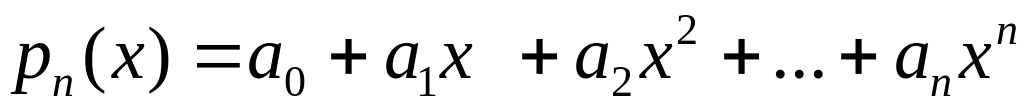 .
Размерность этого
пространства
.
Размерность этого
пространства
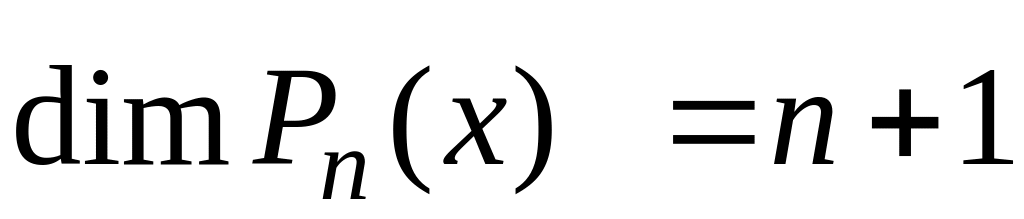 ,
следовательно, базис состоит из
,
следовательно, базис состоит из
 векторов. В качестве базисных векторов
можно выбрать степени переменной
:
векторов. В качестве базисных векторов
можно выбрать степени переменной
:
![]()
![]()
![]()
![]()
……………………..
![]()
 .
Множество
.
Множество
 всех функций
всех функций
 от одной независимой переменной
,
определенных и непрерывных на отрезке
от одной независимой переменной
,
определенных и непрерывных на отрезке
 .
.
Размерность этого
пространства
![]() ,
следовательно, базис состоит из
бесконечного (счетного) количества
векторов. В качестве базисных векторов
можно выбрать степени переменной
от нулевой степени до сколь угодно
большой:
,
следовательно, базис состоит из
бесконечного (счетного) количества
векторов. В качестве базисных векторов
можно выбрать степени переменной
от нулевой степени до сколь угодно
большой:
………..
……….
Примечание: Если в линейном пространстве могут существовать линейно независимые системы векторов с любым количеством векторов, то в этом случае его размерность считается бесконечной.
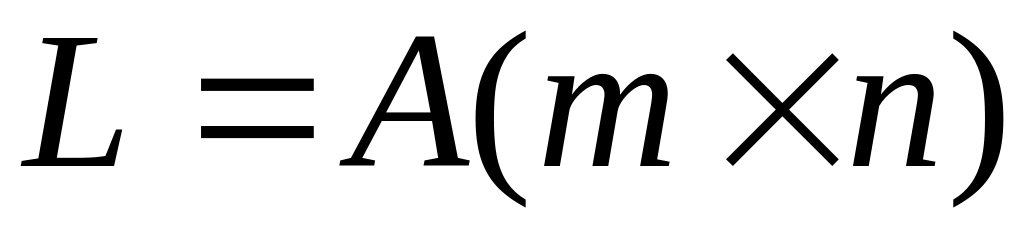 .
Множество
.
Множество
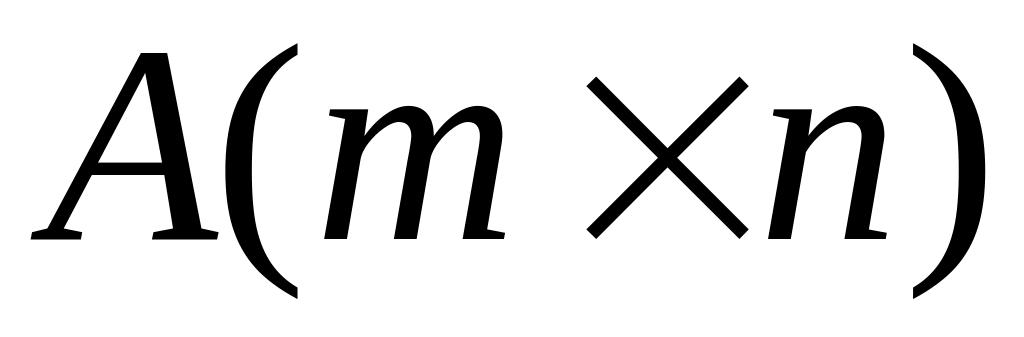 матриц порядка
матриц порядка
 является линейным пространством.
Размерность этого пространства
является линейным пространством.
Размерность этого пространства
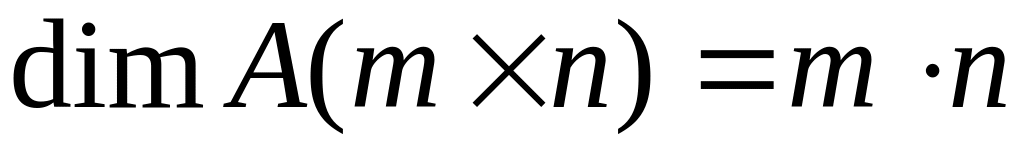 ,
,
Рассмотрим линейное
пространство квадратных матриц
![]() .
Его размерность
.
Его размерность
![]() .
В качестве четырех базисных векторов
можно выбрать базис Вейля, состоящий
из следующих матриц:
.
В качестве четырех базисных векторов
можно выбрать базис Вейля, состоящий
из следующих матриц:
![]() ,
,
![]() ,
,
![]() ,
,
![]() .
.
ЛЕКЦИЯ 5
Подпространство и линейная оболочка. Операции над линейными пространствами. Изоморфизм линейных пространств.
-
«Черепаху догонит только тот Ахилл, который ее уже догнал»
ТЕОРЕМА 7. В данном базисе координаты вектора определены однозначно.
Доказательство. (От обратного).
Предположим, что существует два набора координат вектора в данном базисе . Имеем следующие два разложения
(а)
![]() (б)
(б)
Вычитаем (б) из (а)
![]() .
.
Так как базис является линейно-независимой системой векторов, то их нулевая линейная комбинация является тривиальной, т.е.
![]()
Следовательно
наборы координат совпадают:
![]() ,
,
![]() .
.
Подпространство и линейная оболочка. Операции над линейными пространствами.
Рассмотрим в
множестве
некоторое его подмножество
![]() ,
,
![]() .
.
Пусть множество является линейным пространством. Установим условия при которых является линейным подпространством в пространстве .
ОПРЕДЕЛЕНИЕ. Подмножество является линейным подпространством в пространстве , если выполнены два условия:
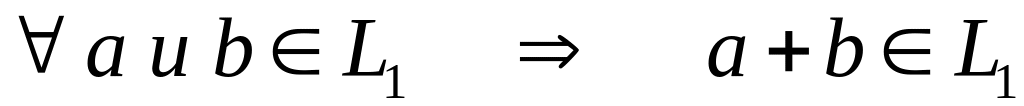 ;
;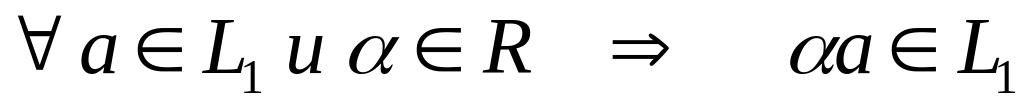 ;
;
Выполнение этих двух условий означает, что при сложении векторов из множества и умножения вектора на число получается вектор, который принадлежит подмножеству . Следовательно, подмножество будет подпространством.
Рассмотрим некоторую
систему векторов
![]() .
.
ОПРЕДЕЛЕНИЕ.
Линейной
оболочкой
системы векторов
![]() называется множество всевозможных
линейных комбинаций этих векторов:
называется множество всевозможных
линейных комбинаций этих векторов:
![]()
Введем обозначение
линейной оболочки
![]() :
:
=![]()
Всякая линейная оболочка является подпространством в .
О размерности линейной оболочки:
![]() числу линейно
независимых векторов системы
числу линейно
независимых векторов системы
векторов
Пример.
Рассмотрим систему из 5-ти векторов:
![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
,
![]() .
Найдем размерность линейной оболочки
системы векторов
.
Найдем размерность линейной оболочки
системы векторов
![]() Для этого рассмотрим матрицу, составленную
из координат данных векторов, и найдем
ее ранг:
Для этого рассмотрим матрицу, составленную
из координат данных векторов, и найдем
ее ранг:
![]() ,
,
![]()
Базисный минор матрицы составлен из первой, второй и пятой строк.
Следовательно,
![]()
Ответ: размерность линейной оболочки равна 3.
