Лекция 6 лекция 7

Преобразование вектора при преобразовании базиса. Системы линейных уравнений. Теорема Кронекера-Капелли. Формула Крамера. Фундаментальная система решений.

«…мышление строится таким образом, что даже если начала кажутся неверными, то следствия и выводы, полученные на основе этих начал будут всегда истинными» Р.Декарт, «Начала философии»

Преобразование вектора при преобразовании базиса

Рассмотрим линейное пространство , .

Выберем в два базиса:

базис , назовем его старым базисом;

базис , назовем этот базис новым;

Выполним разложение векторов старого базиса по новому базису

(1)

……………………………………………………….

или в компактной форме: ; (1а)

Соотношения (1) и (1а) определяют матрицу , которая называется матрицей преобразования базисов.

Рассмотрим некоторый вектор в старом и новом базисах:

(2)

(2а)

где - координаты вектора в старом базисе, - координаты вектора в новом базисе. Выполним преобразование – подставим (1а) в (2а)

Отсюда следует , или

…………………………………………

В итоге - преобразование базисов и координат.

Системы линейных уравнений

Рассмотрим систему из - уравнений, содержащую - неизвестных

Матричный вид записи системы уравнений:

.

Введем основную матрицу , расширенную матрицу ,

,

столбец неизвестных и столбец правой части уравнения

, .

Классификация уравнений:

- неоднородная система уравнений, если .

- однородная система уравнений, если .

Классификация решений:

• Система уравнений называется совместной, если имеет решение.

• Система уравнений несовместна, если не имеет решений.

ТЕОРЕМА 12. Кронекера-Капелли.

Для того, чтобы система уравнений была совместной (имела решение) необходимо и достаточно, чтобы совпадали ранги основной и расширенной матриц: .

Необходимость. Пусть совместна, т.е. имеет решение и

Рассмотрим столбцы матрицы . По теореме о базисном миноре любой столбец этой матрицы является линейной комбинацией ее базисных столбцов. Столбец является линейной комбинацией столбцов матрицы и ее базисных столбцов:

,

где - столбцы матрицы . Следовательно, .

Достаточность. Пусть . В этом случае система уравнений будет совместна. Докажем это. Очевидно, что базисных столбцов матрицы будут базисными и для матрицы . Следовательно, столбец не входит в число базисных столбцов и, согласно теореме о базисном миноре, будет некоторой линейной комбинацией базисных столбцов столбцов матрицы Это означает, что существуют некоторые числа , такие что

,

В результате набор чисел будет являться решением системы уравнений.

Формула Крамера

Рассмотрим квадратную систему уравнений: - уравнений с - неизвестными

Пусть . Тогда и система уравнений совместна. Кроме того, у матрицы существует обратная матрица. Решая матричное уравнение , получаем

Это и есть формула Крамера в матричном виде. Чаще формулу Крамера записывают в следующем виде

, где , - определитель матрицы , в которой столбец заменен на столбец .

Фундаментальная система решений.

Рассмотрим однородную систему уравнений: .

1. Однородная система уравнений всегда совместна: так как столбец , то .

2. Всегда существует нулевое решение 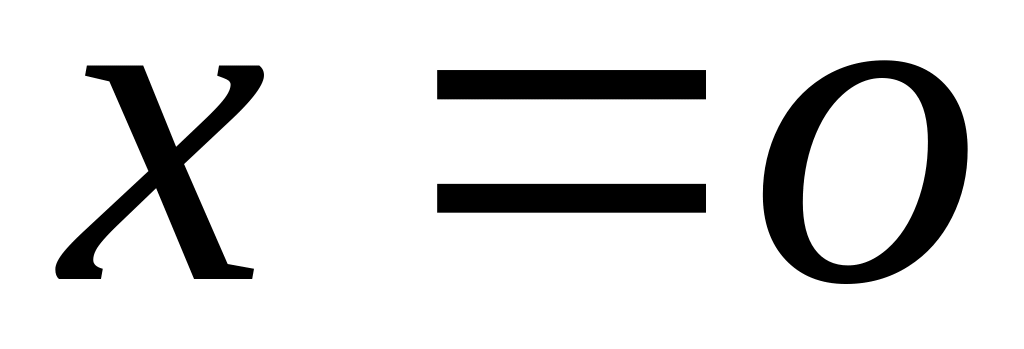, . Нулевое решение называется тривиальным решением.

3. Основная задача – найти условия, при которых однородная система уравнений будет иметь нетривиальное решение (ненулевое решение).

Столбец , составленный из неизвестных

мы будем рассматривать, как вектор -мерного линейного пространства. В этом случае систему уравнений можно интерпретировать следующим образом: матрица переводит вектор в нулевой вектор .

ТЕОРЕМА 13. Однородная система -уравнений с -неизвестными имеет нетривиальное решение тогда и только тогда, когда .

Доказательство. Рассмотрим однородную систему уравнений

Запишем систему уравнений в виде линейной комбинации столбцов матрицы :

Очевидно, если среди чисел найдутся ненулевые, то эти столбцы будут линейно-зависимыми (вспомним определение линейной зависимости системы векторов). Тогда, в силу теоремы о базисном миноре , т.е. из столбцов матрицы, только столбцов являются базисными. В результате мы получили условие существования нетривиального решения и доказали теорему.

Следствие. Для квадратной системы уравнений , нетривиальное решение будет при так как это условие эквивалентно условию .

Найдем нетривиальное решение .

Пусть и базисный минор расположен в правом верхнем углу матрицы . Следовательно, первые столбцов являются базисными.

По теореме о линейной зависимости, один из столбцов линейно выражается через остальные, а значит и через базисные столбцы (см. теорему о базисном миноре). Преобразуем систему уравнений, оставив в левой части уравнения базисные столбцы и перенеся остальные на право

Систему уравнений запишем в матричном виде , где матрица

является квадратной порядка , причем . Далее используем формулу Крамера и получаем решения.

где - произвольные.

Выберем следующие наборы произвольных

, комбинаций.

В результате мы получим частных решений , которые запишем в виде строк

Эти частные решения системы уравнений представляют собой линейно-независимую систему векторов линейного пространства.

Определение. Система частных линейно-независимых решений называется фундаментальной системой решений соответствующей однородной системы уравнений.

Определение. Общим решением однородной системы уравнений называется всякая линейная комбинация векторов фундаментальной системы решений

Общее решение записано, как линейная оболочка частных решений, или векторов.

Так как частные решения - линейно-независимая система векторов, то они образуют базис пространства решений. В результате, постановка задачи: решить однородную систему уравнений, проводит нас к понятию пространства решений однородной системы уравнений.