9. Метод случайного поиска. Алгоритм покоординатного обучения.

Особенность метода в том, что в процессе вычисления приближений x^k используются случайные вектора в качестве направления движения. Например,

x^{k + 1} = x^k + α_kξ, k=0,1,..., (1)

где α^k > 0 – длина шага, ξ = (ξ1,..., ξn) – реализация n-мерной случайной величины ξ с заданным распределением. Например, ξi – независимые случайные величины, равномерно распределенные на отрезке [-1, 1]. Т.о, любая реализация метода случайного поиска использует генератор случайных чисел, который по любому запросу выдает реализацию случайного вектора ξ с заданной функцией распределения.

Рассмотрим задачу f(x) → min_x∈Q, где Q⊆Rⁿ_. Пусть известно k-ое приближение x^k∈Q, k=0,1,… .

Пусть ξ(w) = (ξ₁(w),..., ξ_n(w)) – семейство случайных векторов, зависящих от параметров w = (w₁,..., w_n). Для каждого случайная величина ξi=1 с вероятностью pi и ξi= –1 с вероятностью (1-pi), где

Пусть x⁰ задано, x¹ вычисляется по формуле

x^{k + 1} = x^k + α_kξ_k, k=0 (1)

где берется какая-либо реализация случайного вектора ξ₀=ξ(0) для значений параметров w₀=(0,…,0). Приближение x² также вычисляется по этой формуле при k=1 с помощью вектора ξ₁=ξ(0)

Пусть известны приближения x⁰, x¹,…,x^k и значения параметров

w^k-1 = (w₁ ^k-1,..., w_n ^k-1), где k >= 1. Положим

(2)

где i=1,…,n, k=2,3,…

С помощью параметра управляют памятью алгоритма. Параметр управляет скоростью обучения, при этом предполагается, что величины и не могут быть равными нулю одновременно. Приближение x^k+1 определяется по формуле (1) для реализации случайного вектора ξ_k=ξ(w^k) для набора значений параметров w^k = (w₁ ^k,..., w_n ^k).

Из формул для вычисления вероятностей pi и параметров следует что, если , то вероятность выбора направления на следующем шаге увеличивается. В противном случае эта вероятность падает. Итак, с помощью формул (2) происходит обучение алгоритма.

Величина в (2) регулирует влияние предыдущих значений параметров на обучение; при 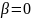влияние предыдущих состояний не учитывается. Величина в (2) регулирует скорость обучения; при бучения не происходит.

10. Градиентный метод. Метод с постоянным шагом.

Основная идея метода заключается в том, чтобы осуществлять оптимизацию в направлении наискорейшего спуска, а это направление задаётся антиградиентом :

где выбирается

• постоянной, в этом случае метод может расходиться;

• дробным шагом, т.е. длина шага в процессе спуска делится на некое число;

• наискорейшим спуском:

Сходимость градиентного спуска с постоянным шагом

Теорема 1 о сходимости метода градиентного спуска спуска с постоянным шагом.

Пусть , функция f дифференцируема, ограничена снизу. Пусть выполняется условие Липшица для градиента : : . Пусть .

Тогда при любом выборе начального приближения.

В условиях теоремы градиентный метод обеспечивает сходимость либо к точной нижней грани (если функция f(x) не имеет минимума) либо к значению Существуют примеры, когда в точке x* реализуется седло, а не минимум. Тем не менее, на практике методы градиентного спуска обычно обходят седловые точки и находят локальные минимумы целевой функции.

Определение. Дифференцируемая функция f называется сильно выпуклой (с константой ), если для любых x и y из Rⁿ справедливо

Теорема 2 о сходимости метода градиентного спуска спуска с постоянным шагом.

Пусть функция f дифференцируема, сильно выпукла с константой . Пусть выполняется условие Липшица для градиента : . Пусть .

Тогда при любом выборе начального приближения.