
- •Элементы выпуклого анализа.
- •Начальные сведения о численных методах оптимизации.
- •4.Сходимость методов оптимизации.
- •5.Метод покоординатного спуска.
- •6.Метод случайного поиска. Алгоритм с возвратом при неудачном шаге.
- •7. Метод случайного поиска. Алгоритм наилучшей пробы.
- •8. Метод случайного поиска. Алгоритм статистического градиента.
- •9. Метод случайного поиска. Алгоритм покоординатного обучения.
- •10. Градиентный метод. Метод с постоянным шагом.
- •11. Градиентный метод. Метод с дроблением шага.
- •12. Градиентный метод. Метод наискорейшего спуска.
- •13. Метод Ньютона
- •14. Численные методы решения задач линейного программирования. Прямой симплекс-метод. Базис и базисное решение.
- •15. Численные методы решения задач линейного программирования. Прямой симплекс-метод. Элементарные преобразования. Симплекс-таблицы.
- •16. Численные методы решения задач линейного программирования. Прямой симплекс-метод. Алгоритм симплекс-метода.
- •17. Численные методы решения задач линейного программирования. Модифицированный симплекс-метод.
- •18. Численные методы решения задач линейного программирования. Лексикографический прямой симплекс-метод
- •19. Численные методы решения задач линейного программирования. Двойственный симплекс-метод.
- •20. Численные методы решения задач линейного программирования. Двойственный симплекс-метод.
- •22. Численные методы решения задач линейного программирования. Геометрическая интерпретация задач линейного программирования
- •23. Численные методы решения задач линейного программирования. Геометрическая интерпретация прямого симплекс-метода.
- •24. Численные методы условной оптимизации. Метод возможных направлений.
- •25. Численные методы условной оптимизации. Метод Келли и метод секущих плоскостей.
- •26. Численные методы условной оптимизации. Первый (циклический) алгоритм Гомори.
- •27. Численные методы условной оптимизации. Метод ветвей и границ
- •28. Численные методы условной оптимизации. Метод ветвей и границ для решения задач нелинейного программирования
- •29. Численные методы условной оптимизации. Метод внешних штрафов
- •30.Численные методы условной оптимизации. Метод внутренних штрафов или метод барьерных функций
- •31.Муравьиный алгоритм.
- •32.Генетические алгоритмы.
- •33.Задачи классического вариационного исчисления. Постановка задачи классического вариационного исчисления
- •Сильный и слабый экстремум в задачах классического вариационного исчисления.
- •Допустимые управления и управляемые процессы в задачах оптимального управления. Оптимальные процессы
- •Элементарный вывод необходимых условий экстремума для простейших задач классического вариационного исчисления
- •Задачи оптимального управления. Постановка задачи оптимального управления
- •Формулировка принципа максимума для линейной задачи быстродействия
- •Доказательство принципа максимума для линейной задачи быстродействия.
- •Достаточность принципа максимума
Элементарный вывод необходимых условий экстремума для простейших задач классического вариационного исчисления
В этом параграфе дается вывод необходимых условий Эйлера. Дальнейшие рассуждения всюду основаны на непосредственном применении метода вариаций.
Начнем с простейшей задачи вариационного исчисления с закрепленными концами:
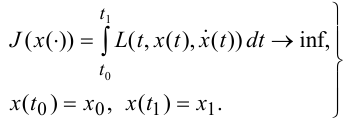 (11)
(11)
Предположим, что функция L(t,x,y) непрерывно дифференцируема в некоторой области U пространства R3. Задачу (11) будем исследовать на слабый экстремум, то есть в пространстве C1([t0,t1]) .
Вывод уравнения Эйлера состоит из трех этапов.
Первый этап состоит в доказательстве того, что функционал J обладает
первой вариацией
в любой точке x*(.) такой, что точки
![]() ,
,
![]() ,
принадлежат области U , и в получении
необходимого условия в
,
принадлежат области U , и в получении
необходимого условия в
терминах первой вариации. Рассмотрим функцию одной переменной
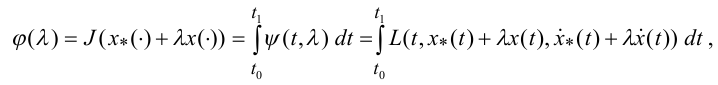 (12)
(12)
порожденную
вариацией
![]() точки
точки
![]() по
направлению
по
направлению
точки
![]() .
При наших допущениях относительно L,
и
функция
.
При наших допущениях относительно L,
и
функция
![]() является
дифференцируемой по
при достаточно малых
, и при этом производная
является
дифференцируемой по
при достаточно малых
, и при этом производная
![]() непрерывна, так как
непрерывна, так как
![]()
![]() Следовательно,
допустимо дифференцирование в (12) под
знаком интеграла и при этом
Следовательно,
допустимо дифференцирование в (12) под
знаком интеграла и при этом
![]() где
где
![]() Так
как исследуемая функция x*(t) допустима,
то для любой функции xt (), принадлежащей
подпространству
Так
как исследуемая функция x*(t) допустима,
то для любой функции xt (), принадлежащей
подпространству
![]() =0
}, функция
=0
}, функция
![]() будет проходить через те же граничные
точки, что и функция x*(t) . Следовательно,
если x*(t) есть решение задачи (11), то при
условии,
будет проходить через те же граничные
точки, что и функция x*(t) . Следовательно,
если x*(t) есть решение задачи (11), то при
условии,
![]() , функция, определяемая соотношением
(12), должна иметь минимум в точке нуль.
В итоге получаем необходимое условие
экстремума
, функция, определяемая соотношением
(12), должна иметь минимум в точке нуль.
В итоге получаем необходимое условие
экстремума
![]() (13). Первый этап вывода
закончен.
(13). Первый этап вывода
закончен.
Второй этап
состоит в преобразовании выражения для
первой вариации на пространстве L0
посредством интегрирования по частям.
Делают это двумя способами: следуя
Лагранжу, когда интегрируют по частям
второе слагаемое, и, следуя Дюбуа-Раймону,
когда интегрируют первое слагаемое.
Преобразование по Лагранжу предполагает
дополнительное условие гладкости, а
именно, допущение, что функция
![]() является
непрерывно дифференцируемой. При этом
дополнительном предположении
проинтегрируем по частям второе слагаемое
в выражении для первой вариации при
условии, что
является
непрерывно дифференцируемой. При этом
дополнительном предположении
проинтегрируем по частям второе слагаемое
в выражении для первой вариации при
условии, что
![]() .
Получим:
.
Получим:
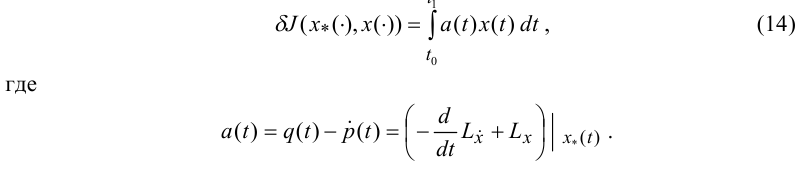 Приведем
теперь преобразование первой вариации
по Дюбуа-Раймону. Для этого проинтегрируем
по частям первое слагаемое на пространстве
L0:
Приведем
теперь преобразование первой вариации
по Дюбуа-Раймону. Для этого проинтегрируем
по частям первое слагаемое на пространстве
L0:
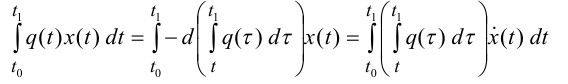
и получим, что выражение для первой вариации имеет следующий вид:
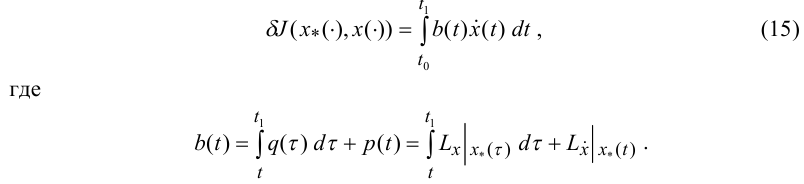
Переходим к третьему этапу вывода уравнения Эйлера.
Лемма 1 (Лагранжа). Пусть функция a(t) непрерывна на отрезке [t0,t1]. Предположим, что для любой непрерывно дифференцируемой функции x(t) ,обращающейся в нуль на концах отрезка [t0,t1] , выполнено равенство
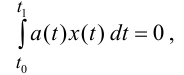 тогда
a(t)
= 0 .
тогда
a(t)
= 0 .
Лемма 2 (Дюбуа-Раймона). Пусть функция b(t) непрерывна на отрезке [t0,t1]. Предположим, что для любой непрерывной функции v(t), в среднем равной нулю, выполнено равенство
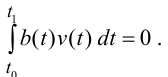 Тогда
b(t) = b0 = const .
Тогда
b(t) = b0 = const .
Следствие 1.
Пусть в задаче (11) лагранжиан L непрерывно
дифференцируем в некоторой области
![]() такой,
что ей принадлежат точки
такой,
что ей принадлежат точки
![]() .
Для того чтобы функция x*(t)
доставляла слабый локальный минимум в
задаче (11), необходимо, чтобы было
выполнено уравнение Эйлера в форме
Лагранжа:
.
Для того чтобы функция x*(t)
доставляла слабый локальный минимум в
задаче (11), необходимо, чтобы было
выполнено уравнение Эйлера в форме
Лагранжа:
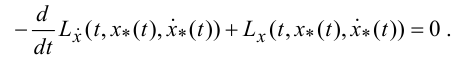 (16).
Функции x*(t) , вдоль которых выполнено
уравнение Эйлера, называются экстремалями.
Приведем несколько частных случаев,
когда у уравнения Эйлера имеются
интегралы.
(16).
Функции x*(t) , вдоль которых выполнено
уравнение Эйлера, называются экстремалями.
Приведем несколько частных случаев,
когда у уравнения Эйлера имеются
интегралы.
Следствие 2.
Если функция L не зависит от x, то для
экстремальности x*(t)
необходимо, чтобы было выполнено
соотношение
![]()
Следствие 3. Если функция L не зависит от x , то уравнение Эйлера допускает интеграл импульса:
![]()
Следствие 4. Если функция L не зависит от t, то уравнение Эйлера допускает интеграл энергии:
![]() Следствия
1 и 2 непосредственно вытекают из (16). Для
доказательства следствия 3 надо взять
производную
Следствия
1 и 2 непосредственно вытекают из (16). Для
доказательства следствия 3 надо взять
производную
![]() и, воспользовавшись (16), показать,
что она
равна нулю.
и, воспользовавшись (16), показать,
что она
равна нулю.
