
- •Элементы выпуклого анализа.
- •Начальные сведения о численных методах оптимизации.
- •4.Сходимость методов оптимизации.
- •5.Метод покоординатного спуска.
- •6.Метод случайного поиска. Алгоритм с возвратом при неудачном шаге.
- •7. Метод случайного поиска. Алгоритм наилучшей пробы.
- •8. Метод случайного поиска. Алгоритм статистического градиента.
- •9. Метод случайного поиска. Алгоритм покоординатного обучения.
- •10. Градиентный метод. Метод с постоянным шагом.
- •11. Градиентный метод. Метод с дроблением шага.
- •12. Градиентный метод. Метод наискорейшего спуска.
- •13. Метод Ньютона
- •14. Численные методы решения задач линейного программирования. Прямой симплекс-метод. Базис и базисное решение.
- •15. Численные методы решения задач линейного программирования. Прямой симплекс-метод. Элементарные преобразования. Симплекс-таблицы.
- •16. Численные методы решения задач линейного программирования. Прямой симплекс-метод. Алгоритм симплекс-метода.
- •17. Численные методы решения задач линейного программирования. Модифицированный симплекс-метод.
- •18. Численные методы решения задач линейного программирования. Лексикографический прямой симплекс-метод
- •19. Численные методы решения задач линейного программирования. Двойственный симплекс-метод.
- •20. Численные методы решения задач линейного программирования. Двойственный симплекс-метод.
- •22. Численные методы решения задач линейного программирования. Геометрическая интерпретация задач линейного программирования
- •23. Численные методы решения задач линейного программирования. Геометрическая интерпретация прямого симплекс-метода.
- •24. Численные методы условной оптимизации. Метод возможных направлений.
- •25. Численные методы условной оптимизации. Метод Келли и метод секущих плоскостей.
- •26. Численные методы условной оптимизации. Первый (циклический) алгоритм Гомори.
- •27. Численные методы условной оптимизации. Метод ветвей и границ
- •28. Численные методы условной оптимизации. Метод ветвей и границ для решения задач нелинейного программирования
- •29. Численные методы условной оптимизации. Метод внешних штрафов
- •30.Численные методы условной оптимизации. Метод внутренних штрафов или метод барьерных функций
- •31.Муравьиный алгоритм.
- •32.Генетические алгоритмы.
- •33.Задачи классического вариационного исчисления. Постановка задачи классического вариационного исчисления
- •Сильный и слабый экстремум в задачах классического вариационного исчисления.
- •Допустимые управления и управляемые процессы в задачах оптимального управления. Оптимальные процессы
- •Элементарный вывод необходимых условий экстремума для простейших задач классического вариационного исчисления
- •Задачи оптимального управления. Постановка задачи оптимального управления
- •Формулировка принципа максимума для линейной задачи быстродействия
- •Доказательство принципа максимума для линейной задачи быстродействия.
- •Достаточность принципа максимума
7. Метод случайного поиска. Алгоритм наилучшей пробы.
Особенность метода в том, что в процессе вычисления приближений xk используются случайные вектора в качестве направления движения. Например,
xk + 1 = xk + αkξ, k=0,1,..., (1)
где αk > 0 – длина шага, ξ = (ξ1,..., ξn) – реализация n-мерной случайной величины ξ с заданным распределением. Например, ξi – независимые случайные величины, равномерно распределенные на отрезке [-1, 1]. Т.о, любая реализация метода случайного поиска использует генератор случайных чисел, который по любому запросу выдает реализацию случайного вектора ξ с заданной функцией распределения.
Рассмотрим задачу f(x) → minx∈Q, где Q⊆Rn. Пусть известно k-ое приближение xk∈Q, k=0,1,… .
Решение по алгоритму наилучшей пробы.
Пусть ξ1,..., ξs – реализации случайного вектора ξ. Величины α и s > 1 являются параметрами алгоритма. Пусть i0 – индекс, определяемый условием

Далее
полагаем 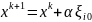
8. Метод случайного поиска. Алгоритм статистического градиента.
Особенность метода в том, что в процессе вычисления приближений xk используются случайные вектора в качестве направления движения. Например,
xk + 1 = xk + αkξ, k=0,1,..., (1)
где αk > 0 – длина шага, ξ = (ξ1,..., ξn) – реализация n-мерной случайной величины ξ с заданным распределением. Например, ξi – независимые случайные величины, равномерно распределенные на отрезке [-1, 1]. Т.о, любая реализация метода случайного поиска использует генератор случайных чисел, который по любому запросу выдает реализацию случайного вектора ξ с заданной функцией распределения.
Рассмотрим задачу f(x) → minx∈Q, где Q⊆Rn. Пусть известно k-ое приближение xk∈Q, k=0,1,… .
Решение по алгоритму статистического градиента.
Пусть ξ1,...,
ξs
– реализации случайного вектора ξ.
Вычислить разности
 для всех
для всех
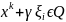 ,
,
 .
Пусть
.
Пусть

Если
 ,
то
,
то
 .
В противном случае выбрать новый набор
ξ’1,...,
ξ’s
реализаций случайного вектора ξ
и повторить действия.
.
В противном случае выбрать новый набор
ξ’1,...,
ξ’s
реализаций случайного вектора ξ
и повторить действия.
Величины s>1, a>0, g>0 – параметры алгоритма, γ – длина шага сетки. Вектор pk – статистический градиент. Если Q=Rn ,s=n и векторы ξi равны единичным векторам ei , i=1,…, s, то данный алгоритм оказывается разностным аналогом градиентного метода.
Так как функция распределения случайного вектора ξ не зависит от номера итерации, то предложенные выше варианты метода случайного поиска называют методами случайного поиска без обучения. Эти алгоритмы не обладают способностью учитывать результаты предыдущих итераций и, обнаруживать более перспективные направления убывания минимизируемой функции. Как результат, они медленно сходятся. Методы случайного поиска, которые обладают способностью приспосабливаться к конкретным особенностям минимизируемой функции, назовем методами случайного поиска с обучением. Так как в этом случае функция распределения вектора ξ пересчитывается в зависимости от номера итерации и предыдущих результатов, то итерационный процесс (1) записывается теперь в виде
xk + 1 = xk + αkξk, k=0,1,..., (2)
На нулевой итерации функция распределения вектора ξ выбирается с учетом априорной информации о целевой функции. Если такая информация недоступна, то нулевую итерацию начинают со случайного вектора
ξ0 = (ξ01,..., ξ0n), где ξ01,..., ξ0n – независимые случайные величины, равномерно распределенные на отрезке [- 1 , 1].
