1. Экстремальные задачи.

2. Элементы выпуклого анализа.

3. Начальные сведения о численных методах оптимизации.

4. Сходимость методов оптимизации.

5. Метод покоординатного спуска.

6. Метод случайного поиска. Алгоритм с возвратом при неудачном шаге.

7. Метод случайного поиска. Алгоритм наилучшей пробы.

8. Метод случайного поиска. Алгоритм статистического градиента.

9. Метод случайного поиска. Алгоритм покоординатного обучения.

10. Градиентный метод. Метод с постоянным шагом.

11. Градиентный метод. Метод с дроблением шага.

12. Градиентный метод. Метод наискорейшего спуска.

13. Метод Ньютона.

14. Численные методы решения задач линейного программирования. Прямой симплекс-метод. Базис и базисное решение.

15. Численные методы решения задач линейного программирования. Прямой симплекс-метод. Элементарные преобразования. Симплекс-таблицы.

16. Численные методы решения задач линейного программирования. Прямой симплекс-метод. Алгоритм симплекс-метода.

17. Численные методы решения задач линейного программирования. Модифицированный симплекс-метод.

18. Численные методы решения задач линейного программирования. Лексикографический прямой симплекс-метод

19. Численные методы решения задач линейного программирования. Метод искусственного базиса

20. Численные методы решения задач линейного программирования. Двойственный симплекс-метод.

21. Численные методы решения задач линейного программирования. Лексикографический двойственный симплекс-метод

22. Численные методы решения задач линейного программирования. Геометрическая интерпретация задач линейного программирования

23. Численные методы решения задач линейного программирования. Геометрическая интерпретация прямого симплекс-метода

24. Численные методы условной оптимизации. Метод возможных направлений.

25. Численные методы условной оптимизации. Метод Келли и метод секущих плоскостей.

26. Численные методы условной оптимизации. Первый (циклический) алгоритм Гомори.

27. Численные методы условной оптимизации. Метод ветвей и границ

28. Численные методы условной оптимизации. Метод ветвей и границ для решения задач нелинейного программирования

29. Численные методы условной оптимизации. Метод внешних штрафов

30. Численные методы условной оптимизации. Метод внутренних штрафов или метод барьерных функций

31. Муравьиный алгоритм.

32. Генетические алгоритмы.

33. Задачи классического вариационного исчисления. Постановка задачи классического вариационного исчисления

34. Сильный и слабый экстремум в задачах классического вариационного исчисления

35. Допустимые управления и управляемые процессы в задачах оптимального управления. Оптимальные процессы

36. Элементарный вывод необходимых условий экстремума для простейших задач классического вариационного исчисления

37. Задачи оптимального управления. Постановка задачи оптимального управления

38. Формулировка принципа максимума для линейной задачи быстродействия

39. Доказательство принципа максимума для линейной задачи быстродействия.

40. Достаточность принципа максимума.

1. Экспериментальный задачи

Задачи отыскания наибольших или наименьших величин часто возникают в науке, технике и экономике. Чтобы применять математические методы для их решения и анализа, необходимо уметь переходить от содержательной к математической постановке задачи. Для этого нужно определить целевую функцию f , множество допустимых решений Q для функции f и критерий оптимизации extr ϵ {min, max} . Таким образом, тройка вида ( f ,Q, extr) задает экстремальную или оптимизационную задачу. Формально математическая постановка выглядит следующим образом: 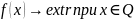. Учитывая равенство min f (x) = - max( -f (x)) при , в дальнейшем ограничимся рассмотрением только задач минимизации. Будем говорить, что задача минимизации решена, если

1. либо найдено ее оптимальное решение, то есть точка 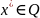такая, что f (x*) ≤ f (x) для всех . Символически это записывается в виде равенства при

2. либо найден конечный инфинум при целевой функции на множестве Q в случае, когда оптимального решения не существует;

3. либо доказано, что целевая функция неограниченна снизу на множестве допустимых решений;

4. либо установлено, что множество допустимых решений пусто.

Далее будем рассматривать экстремальные задачи, в которых допустимое множество задается в следующем виде: Q = {x ϵ S | φ_i (x) ≤ 0, i = 1,…,m} , где S является либо подмножеством пространства Rⁿ , либо подмножеством Zⁿ ,либо – Bⁿ . Функции φ_i(x), i = 1, …,m, – скалярные функции со значениями в R . Выражения x ϵ S, φ_i(x) ≤ 0, i = 1, …,m – называются ограничениями оптимизационной задачи. Ограничения вида φ_i(x) ≤ 0, i = 1, …,m, называются функциональными, а ограничение x ϵ S называется ограничением типа включения. Различие между функциональными и нефункциональными ограничениями условно, так как каждое включение можно записать как функциональное ограничение и, наоборот. Одновременное использование этих ограничений делает постановку задачи более структурированной и, следовательно, более наглядной. Формально экстремальная задача в этом случае записывается в следующем виде: 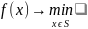, φ_i(x) ≤ 0, i = 1, …,m

В зависимости от природы множества S экстремальные задачи классифицируются как:

· дискретные или комбинаторные, если множество S конечно или счетно;

· целочисленные, если S 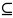Z ⁿ ;

· булевы, если S Bⁿ ;

· вещественные, если S Rⁿ ;

· бесконечномерные, если S – подмножество гильбертова пространства.

Если S = Rⁿ , или S = Z ⁿ , или S = Bⁿ и отсутствуют ограничения φ_i(x) ≤ 0, i = 1, …,m, то есть m = 0 , тогда экстремальная задача называется задачей безусловной оптимизации. В противном случае говорят о задаче условной оптимизации.

Если принять во внимание свойства целевой функции f и ограничений φ_i(x) ≤ 0, i = 1,…,m, то возникает более тонкое деление конечномерных экстремальных задач на классы:

· непрерывное (математическое) программирование (f , φ_i(x), i = 1,…,m, – непрерывные, произвольные, нелинейные функции, S – связное, компактное подмножество Rn );

· дискретное (математическое) программирование (f, φ_i(x), i = 1,…,m, – нелинейные функции, S – дискретное множество);

· нелинейное целочисленное программирование (f, φ_i(x), i = 1,…,m, – нелинейные функции, S Z ⁿ);

· непрерывная нелинейная оптимизация без ограничений (f – непрерывная, произвольная, нелинейная функция, m = 0 , S = Rⁿ);

· целочисленная нелинейная оптимизация без ограничений (f – произвольная, нелинейная функция, m = 0 , S = Z ⁿ);

· выпуклое программирование (f, φ_i(x), i = 1,…,m, – произвольные, выпуклые функции, S – выпуклое подмножество Rⁿ );

· линейное программирование (f, φ_i(x), i = 1,…,m, – произвольные, линейные функции, S = Rⁿ );

· целочисленное линейное программирование (f, φ_i(x), i = 1,…,m, – произвольные, линейные функции, S Z ⁿ).

При решении каждой оптимизационной задачи возникает три проблемы. Первая из них связана с существованием оптимальных решений задачи. При анализе этой проблемы в ряде случаев может оказаться полезной следующая теорема, с помощью которой можно иногда определить, достигает ли функция своего глобального минимума и максимума.

Теорема 1 (Вейерштрасса). Если функция f(x) определена и непрерывна на замкнутом ограниченном множестве X , то она достигает на этом множестве своих точных верхней и нижней границ.

Условие компактности множества X , использованное в теореме, является довольно жестким. И неприменимо для таких часто встречающихся множеств, как S = Rⁿ или S = 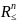. Однако, ослабляя ограничения на множество X и накладывая дополнительные требования на функцию f, из теоремы Вейерштрасса можно получить следующие два следствия.

Следствие 1. Если функция f(x) определена и непрерывна на непустом замкнутом множестве X и для некоторой фиксированной точки v из X множество Лебега M(v) = {x ϵ X | f (x) ≤ f (v)} ограничено, то функция достигает на множестве X своей точной нижней границы.

Следствие 2. Если функция f(x) определена и непрерывна на непустом замкнутом множестве X и для любой последовательности точек 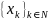из X , для которой 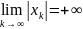, имеет место соотношение 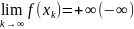, то функция достигает на множестве X своей точной нижней (верхней) границы.

Вторая проблема связана с поиском условий, которым должно удовлетворять оптимальное решение задачи. Третья проблема состоит в том, как найти хотя бы одно такое решение.

Данные проблемы соответствуют разделам теории экстремальных задач, где исследуются вопросы существования оптимальных решений, необходимые и достаточные условия экстремума и численные методы нахождения решений.

2. Элементы выпуклого анализа.

Множество xϵRⁿ называется выпуклым, если λx₁ + (1 - λ)x₂ ϵ X при всех x1, x2 ϵ X ,λ ϵ [0,1] . Иными словами, множество X выпукло, если оно вместе с любыми своими двумя точками x1 и x2 содержит соединяющий их отрезок [x1, x2 ] = {xϵRⁿ | x = x2 +λ (x1 - x2 ), 0 ≤ λ ≤ 1} .

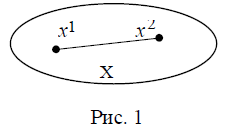(выпуклое) 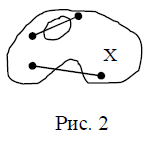(невыпуклое)

На числовой прямой R выпуклыми множествами являются всевозможные промежутки, то есть одноточечные множества, интервалы, полуинтервалы, отрезки, полупрямые, а также сама прямая. Примерами выпуклых множеств в пространстве Rn служат само пространство, любое его линейное подпространство, одноточечное множество, шар, отрезок, а также прямая, проходящая через точку x0 в направлении вектора h , луч, выходящий из точки x0 в направлении вектора h , гиперплоскость с нормалью p и порождаемые ею полупространства. Пустое множество по определению выпуклое. Нетрудно понять, что все перечисленные множества, кроме шара, являются частными случаями выпуклого множества вида

X = {x ϵ Rⁿ | Ax ≤ b} = {x ϵ Rⁿ | ≤ b_i, i = 1,…,m} (1)

где A – некоторая матрица размера m x n со строками a₁,…,a_m , b = (b₁,…,b_m)^T ϵ R^m, m = 1,2,… . Множества вида (1) принято называть полиэдральными или просто полиэдрами. Таким образом, полиэдр – это множество решений некоторой системы конечного числа линейных неравенств. Или, другими словами, пересечение конечного числа полупространств.

Выпуклой комбинацией точек x1,…, xm называется точка

z =a₁x₁ +a₂ x₂ +…+a_mx_m , где a_i ≥ 0 , i = 1,…,m , и a₁ +a₂ +…+ a_m = 1 .

Теорема 2. Выпуклое множество X содержит выпуклые комбинации всех своих точек. Функция f (x) , определенная на выпуклом множестве X ϵ Rⁿ , называется выпуклой на X , если f(λx₁ + (1 - λ)x₂) ≤ λf (x₁) + (1 - λ) f(x₂) (2).

при всех x1, x2 ϵ X , λ ϵ [0,1]. Если при всех x1, x2 ϵ X, x1≠ x2 и λ ϵ (0,1) неравенство (2) выполняется как строгое, то f называется строго выпуклой на X . Функция f называется (строго) вогнутой, если функция (- f ) (строго) выпукла.

Геометрически выпуклость функции f означает, что любая точка произвольной хорды графика f располагается не ниже соответствующей точки самого графика.

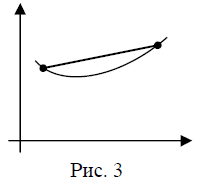
Для вогнутой функции взаимное расположение хорды и графика обратно.

Функцию вида f (x) = 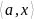+ b , где aϵRⁿ , bϵR будем называть линейной. Ясно, что для линейной функции неравенство (2) выполняется как равенство. Поэтому она одновременно выпукла и вогнута на Rⁿ , но не строго.

Приведем еще несколько полезных свойств выпуклых функций.

Теорема 3. Выпуклая функция f (x) , определенная на выпуклом множестве X , непрерывна в каждой внутренней точке этого множества.

Теорема 4. Функция f(x), дифференцируемая на выпуклом множестве X, выпукла тогда и только тогда, когда для любых x, yϵ X справедливо 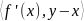≤ f(y) - f(x) .

Теорема 5. Функция f(x) , определенная и дважды непрерывно дифференцируемая на выпуклом множестве X, (строго) выпукла тогда и только тогда, когда матрица 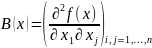(положительно) неотрицательно определена для любого x ϵ X .

Для исследования матрицы B(x) на знакоопределенность используют, как правило, критерий Сильвестра.

Теорема 6. Для любой выпуклой функции f (x) , определенной на выпуклом множестве X , и любого числа λ множество {x ϵ X | f (x) ≤ l} выпукло.

Теорема 7 (неравенство Йенсена). Если функция f (x) выпукла на выпуклом множестве X , то , где x_i ϵ x, a_i ≥ 0, i = 1,…,m , и a1 +a2 +…+am = 1 .

Экстремальная задача , φ_i(x) ≤ 0, i = 1 называется выпуклой, если S – выпуклое множество, f , φ_i(x) ≤ 0, i = 1,…,m, – выпуклые функции на S .

Сформулируем несколько простых утверждений, объясняющих интерес к данному типу задач оптимизации.

Теорема 8. Если экстремальная задача выпукла, то любое ее локальное решение

является также глобальным.

Следующее свойство выпуклых задач можно сформулировать в виде следующего общего принципа: необходимые условия оптимальности в том или ином классе задач оптимизации при соответствующих предположениях выпуклости оказываются и достаточными. Приведем обоснование данного свойства применительно к задаче безусловной оптимизации.

Теорема 9. Пусть функция f выпукла на Rⁿ и дифференцируема в точке x* ϵ Rⁿ. Если f '(x*) = 0 , то x* – точка минимума f на Rⁿ .

Теоремы 8, 9 говорят о том, что для выпуклой задачи отыскание стационарной точки автоматически означает отыскание решения, причем глобального.

Укажем еще одно полезное свойство выпуклых задач.

Теорема 10. Пусть экстремальная задача выпукла и имеет решение. Тогда множество ее решений Q* = Arg min f (x) xϵQ выпукло. Если при этом функция f строго выпукла на множестве Q , то решение задачи единственно.

Большинство теорем о сходимости методов оптимизации доказывается в предположении выпуклости функции, оценки скорости сходимости часто устанавливаются при еще более жестком предположении сильной выпуклости.

Определение 1. Дифференцируемая функция f называется сильно выпуклой (с константой l > 0 ), если для любых x и y из Rⁿ справедливо

f (x + y) ≥ f (x) + 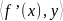+ l

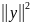
Лемма 1. Если функция f является сильно выпуклой (с константой l > 0 ), то она имеет глобальный минимум на Rⁿ .

Лемма 2. Если функция является сильно выпуклой (с константой l > 0 ) и x* – ее глобальный минимум, то для любого xϵRⁿ выполняется неравенство

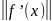≥ 2l( f (x) - f (x*)) .

Лемма 3. Пусть f – дважды непрерывно дифференцируемая функция. Если

f – сильно выпуклая функция с константой l , то выполняется неравенство

|| [ f ’’(x)]^-1 ||≤ l^-1 .