28. Численные методы условной оптимизации. Метод ветвей и границ для решения задач нелинейного программирования

Рассмотрим задачу минимизации нелинейной ф-ции на параллелепипеде где Считаем , что целевая функция f удволетворяет условию Липшица с константой L = const > 0: Из этого следует, что f – непрерывная функция, следовательно, достигает своего минимального значения f* на параллелепипеде. Выберем на отрезке оси j следующие точки где h =2ε /L – шаг сетки, mj – нат. Число, удовлетворяющее неравенству На параллелепипеде Q введем сетку где j координата точки принимает одно из следующих зхначений . Пусть . Теорема: Для любой функции f(x) удовлетворящей уловию Липшица справедлива оценка

Множество является гиперкубом, рассмотрим произвольный гиперкуб из теоремы следует, что для любого верно Функцию выбора наилучшего решения определим на гиперкубах, которые являются атомарными множествами со стороной . Подмножества решений будем задавать в виде набора гиперкубов. На первом шаге имеем , где рекорд -- является центром гиперкуба со стороной .Пусть к следующему шагу есть разбиение и рекорд , проверяем элементы разбиения на наличие решения со значением лучше рекорда. Он считается проверенным и отбрасывается если выполнено одно из сл. условий

1. 2. Стороны гиперкуба Hl не превосходят величины 2ε/L. Если отброшены все элементы разбиения, то алгоритм закончил работу, если не все отброшены то выбираем следующее подмножество и проверяем и т. Д.

29. Численные методы условной оптимизации. Метод внешних штрафов

Общая идея которых заключается в замене решения исходной задачи на решение последовательности экстремальных задач без ограничений. Эти методы интересны тем, что они просты при обосновании сходимости и оказываются практически эффективными при решении оптимизационных задач.

Для функции введем функцию штрафов , очевидно что Следовательно решение задачи равнозначно решению задачи без ограничений.

Метод внешних штрафов.

Функция является штрафной функцией множества Q если и Решение задачи сводится к решению последовательности задач минимизации вида 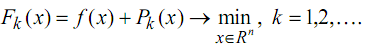Предположим что имеется метод решения херни написанной в последней формуле. Тогда на шаге l+1 найти ее решение с коэфициентом штрафа , если то алгоритм завершен, иначе перейти на следующий шаг.

30.Численные методы условной оптимизации. Метод внутренних штрафов или метод барьерных функций

Представленный ниже алгоритм предназначается для поиска экстремума при наличии ограничений только типа неравенств. Рассмотрим задачу

Опишем в общем виде идею метода штрафов, используемого для решения следующей задачи (1)-(3). Рассмотрим функцию h : R ->R вида:

Определим функцию штрафа Очевидно, что

Следовательно, решение задачи (1)-(3) эквивалентно решению следующей задачи без ограничений

Основной недостаток этого подхода связан с разрывностью функции штрафа H , так как минимизация функции g в этом случае является весьма непростой задачей.

Основной недостаток метода внешних штрафов заключается в том, что оптимум x* аппроксимируется снаружи, то есть приближения x₁ , x₂ ,…, x_l , полученные при коэффициентах штрафа k₁ , k₂ ,…, k_l , не принадлежат множеству допустимых решений задачи, что и послужило причиной создания других методов штрафа, в которых оптимум аппроксимируется изнутри. Этим обосновывается их название – методы внутренних штрафов.

Определение 2. Функция B(x) называется барьерной функцией для Q , если B(x) определена и конечна на Int Q, B(x)>=0 и .

Примеры барьерных функций:

Определим штрафную функцию P_k (x) = a_kB(x) , где a_k – коэффициент штрафа или барьерный коэффициент. Тогда решение задачи (1)-(3) сводится к решению последовательности задач минимизации вида

(24)

Предполагается, что a_k ->0 при k ->∞ . Как и выше, считаем, что существует метод нахождения оптимального решения задачи (24). Пусть x_k = x(k) – оптимальное решение задачи (24) со значением барьерного коэффициента a_k .На практике для решения задачи (24) можно использовать метод градиентов. При этом, если Int Q ≠ и начальное приближение x⁰ Int Q , то можно гарантировать, что все последующие приближения будут принадлежать Int Q. Действительно, рассмотрим итерационную формулу 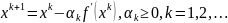. Если в ней текущее приближение x_k Int Q , то при достаточно малой длине шага a_k новое приближение x^{k +1} Int Q.

Рассмотрим итерационный алгоритм. Пусть x^k Int Q – решение задачи (24) на шаге k .

Шаг k + 1 . Находим решение задачи (24) со значением барьерного коэффициента a_{k +1} < a_k . Текущее решение x^k используется в качестве начального приближения. Если , то алгоритм завершает работу. Иначе перейти на следующий шаг.

С практической точки зрения важно, чтобы приближения, которые генерируются в процессе работы алгоритма, сходились к оптимальному решению задачи. Как и в предыдущем случае, возьмем = 0 . Тогда алгоритм порождает бесконечную последовательность приближений. Оказывается, что при достаточно простых предположениях можно гарантировать сходимость этой последовательности к оптимуму.

Предположим, что задача (24) при любом k N достигает минимума на Q и для его вычисления используется один из итерационных методов безусловной оптимизации. Тогда, если начальное приближение x⁰ Int Q , то из свойств барьерной функции следует, что данный алгоритм будет сходится к некоторому значению из множества IntQ . При доказательстве теоремы 6 предполагаем, что множество допустимых решений замкнуто, Int Q ≠ , f C⁰(Rⁿ ) , B C⁰ (IntQ) , B(x) >= 0 , x Int Q и, наконец, для любого элемента x Q существует последовательность {y_k}_{k N} , y_k Int Q, такая, что .

Теорема 6. Пусть выполняется одно из условий:

a) f (x_k) при k для любой последовательности такой, что || x_k || при k ,

б) множество Q ограничено.

Тогда

1) последовательность имеет хотя бы одну предельную точку и любая предельная точка этой последовательности является оптимальным решением,

2) при k .