1. Установление соответствия данной модели

реальным задачам.

Данную модель обычно используют как для анализа задач оценки эффективности решений в условиях неопределенности, так и для антагонистических задач.

• Отличие этих задач заключается в том, что в 1-м случае (неопределенность) У представляет собой неуправляемые (например, природные) факторы.

Во 2-м случае Х и У представляют собой реальных Участников процесса, например, конкурентов.

2) В данной модели предполагается строгий

антагонизм участников.

• Это означает, что интересы участников прямо противоположны.

• При этом считается, что выигрыш 1-го участника в точности равен проигрышу 2-го.

• В реальных задачах в большинстве случаев интересы участников являются несовпадающими, но не антагонистическими. Поэтому применение данной модели становится невозможным.

3) В данной модели для выбора наиболее эффективных решений каждого участника

формируется матрица эффективности Е (Х,У). Т.е. в данном случае используется

однокритериальный подход к решению задач. При решении реальных экономических

задач оценка эффективности принимаемых решений производится с учетом совокупности

показателей.

• Понятие седловой точки

Применение принципа гарантированного результа

• Принцип гарантированного результата является основным принципом принятия

оптимальных решений в условиях антагонизма. В данном случае каждый из участников

р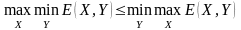 ассчитывает на наихудшие для себя действия другого участника. При этом свои стратегии выбирает оптимальным образом. При использовании данного принципа каждый участник получает гарантированный выигрыш независимо от действий 2-го.

В теории игр доказывается, что

Нижняя граница верхняя граница

Для того, чтобы антагонистические игры были устойчивыми, необходимо, чтобы эти игры

и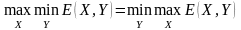 мели седловые точки.

Условие наличия седловой точки:

Наличие седловых точек говорит об устойчивости анализируемых ситуаций для каждого участника. Если седловые точки отсутствуют, то процесс принятия решений становится неустойчивым. При наличии седловых точек (точки) каждому из участников невыгодно от них (нее) отклоняться, т.к. он при этом может только проиграть (не выиграть).

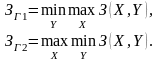В конфликтных ситуациях при использовании теории игр анализируется не матрицы эффективности, а матрицы затрат. Гарантированные затраты каждого изучастников определяются в виде:

У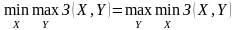 словие наличия седловой точки:

Применение смешанных стратегий в конфликтных ситуациях

Важнейшим условием взаимодействия участников в конфликтных ситуациях является обеспечение устойчивой ситуации равновесия. Эти ситуации называются седловыми точками. При наличии седловых точек выполняется условие:

В этом случае: Цн ≤ Цв

В общем случае данное условие не выполняется. При этом игры участников становятся неустойчивыми и требуется найти способы обеспечения седловых точек. Нейман доказал, что для получения седловых точек в конфликтных ситуациях необходимо применение смешанных стратегий. В отличии от чистых стратегий, при использовании смешанных стратегий, участники применяют не единственную стратегию, а весь набор рассматриваемых стратегий с определенными вероятностями.

Понятие смешанных стратегий

х1, х2, . . . , хn — чистые стратегии

х1, х2, . . . , хn

р1, р2, . . . , рn - смешанные стратегии

П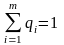 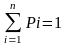ри этом выполняются условия

(стратегии 1-го и 2-го участника):

Особенностью смешанных стратегий является то, что вероятности с которыми применяются чистые стратегии определяются не природными внешними факторами, а самими участниками.

В данном случае функция эффективности участников будет зависеть от вероятностей p и q:

E= f(P,Q) = E(P,Q)

В случае чистых стратегий:  E= φ(X;Y) = E(X;Y)

  В данном случае определяется математическое ожидание функции эффективности:

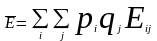
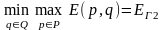Гарантированный выигрыш 1-го участника определяется в виде:

Гарантированный выигрыш 2-го участника:

Н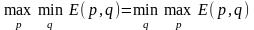 ейман доказал, что путем оптимального подбора смешанных стратегий (вероятностных законов распределения) можно обеспечить наличие седловых точек, при этом всегда будет выполняться условие:

З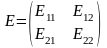 адача 1:

Анализируется матрица:

• Определить смешанную стратегию 1-го участника.

• Будем считать, что 2-ой участник принимает чистую стратегию:

p1*E11+(1-p1)*E21=V

 V – цена игры

p1*E12+(1-p1)*E22=V

p1*E11+(1-p1)*E21=V

p1*E12+(1-p1)*E22=V

p1 = 0

р₂ = 1

Задача 2:

• Будем считать, что 2-ой участник применяет смешанную стратегию, 1-ый — чистую.

q1*E11+(1-q1)*E12=V

q1*E21+(1-q1)*E22=V

Применение смешанных стратегий в экономике

Основное назначение смешанных стратегий заключается в том, чтобы обеспечить наличия седловых точек. Необходимость получения седловых точек обусловлено требованиям получения равновесных ситуаций.При наличии ситуации равновесия, ни одному из участников не целесообразно отклоняться от этих ситуаций, т.к. при этом они обеспечат меньший выигрыш. Основная теорема Неймана заключается в доказательстве того, что при использовании смешанных стратегий, верхняя цена игры равна нижней, т.е. Соблюдается условие наличия с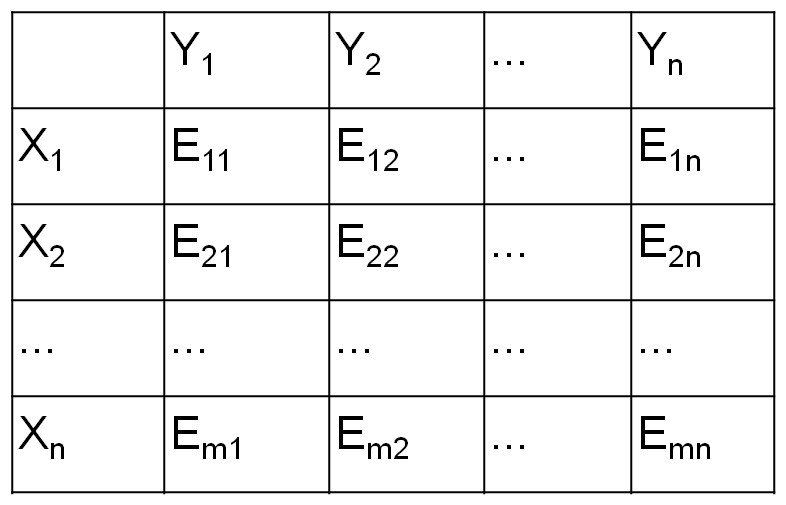 едловой точки.

Применение смешанных стратегий первым участником осуществляется следующим образом: Этот участник ставит задачу определения выигрыша (эффективности) не меньше цены игры V при любой стратегии второго участника.

P1E11 + P2E21 +...+ Em1Pm ≥ V

P1E12 + P2E22 +...+Em2Pm ≥ V (1)

P1E1n + P2E2n +...+EmnPm ≥ V

 

X1E11 + X2E21 +...+ Em1Xm ≥ 1

X1E12 + X2E22 +...+Em2Xm ≥ 1

X 1E1n + X2E2n +...+EmnXm ≥ 1

• Формула (2) представляет собой целевую функцию оптимальной задачи.

• Формула (1) — уравнение ограничения данной задачи.

• Из (1) и (2) следует, что данная задача является линейной задачей оптимизации.

Для решения этой задачи могут быть использованы методы линейного программирования. Вывод:

• Любую задачу, которая описывает конфликтные ситуации и рассматривается в теории игр при использовании смешанных стратегий можно свести к задаче линейного программирования. Решение этой задачи не представляет трудности.

Определение смешанных стратегий с позиции 2-ого участника

q1E11 + q2E12 +...+ qnE1m ≤ V

q1E21 + q2E22 +...+qnE2m ≤ V

q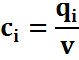 1E1n + q2E2n +...+qnEnm ≤ V

 

С1E11 + C2E12 +...+ CnE1m ≤ 1

C1E21 + C2E22 +...+ CnE2m ≤ 1

C1E1n + C2E2n +...+ CnEmn ≤ 1

Задание:

Сформулировать конфликтную задачу решаемую с помощью теории игр.

Составить матрицу 2х2. Пусть матрица не имеет седловой точки. Применить смешанные стратегии 1-ым участником. Сформулировать задачу линейного программирования.

Дать содержательную трактовку смешанных стратегий.

В реальных экономических задачах возникают сложности, как трактовки смешанных стратегий, так и их применения.

Допустим, что рассматривается известная в литературе задача охраны того или иного объекта от воздушного нападения.

В качестве стратегии противника рассматривают высоколетящих, среднелетящих и низколетящих.

Стратегиями обороняющегося объекта является использование 3-х видов зенитно-ракетных комплексов:

•  низколетящих — ЗРК 1

• среднелетящих — ЗРК 2

• высоколетящих — ЗРК 3

• В качестве функции эффективности может выступать ущерб, в частности экономический.

• Для 1-го участника (обороняющегося) — это будет предотвращенный ущерб.

• Для 2-го — наносимый ущерб.

• Данная задача может быть сведена к задаче линейного программирования.

В результате решения этой задачи находим оптимальные значения смешанных стратегий

• для 1-го участника р⁰₁, р⁰₂, р⁰₃;

• для 2-го q⁰₁, q⁰₂, q⁰₃.

В данном случае возникает вопрос: каким образом реализовать эти смешанные стратегии, т.е. что означает использование ЗРК1, ЗРК2, ЗРК3 с вероятностями р⁰₁, р⁰₂, р⁰_3.

Для устранения трудностей, связанных с применением смешанных стратегий в теории игр, рекомендуется во многих случаях применять так называемые «физические смеси стратегий».

• Задача использования земельных ресурсов

Предположим, что осуществляется конкурс на продажу или сдачи в аренду земельных угодий площадью S. В конкурсе принимают участие 2 конкурсанта. Каждый из участников предлагает конкурсной комиссии несколько вариантов (стратегий) использования этого земельного участка. Тоже самое делает и 2-ой участник, но стратегия отличается.

В качестве стратегии участников могут быть: различные виды выращивания с/х продукции.

Данную задачу можно решить с помощью метода линейного программирования.

При этом определяются вероятности:

р⁰₁, р⁰₂, р⁰₃— для 1-ого

q⁰₁, q⁰₂, q⁰₃— для 2-ого

В данной задаче вместо смешанных стратегий можно применить физическую смесь стратегий каждого участника.

При этом вместо вероятностей p и q использовать площади, отводимые под каждые культуры.

P⁰_i → S⁰_i

q⁰_j → S⁰_j

В данной задаче вместо смешанных стратегий можно применить физическую смесь стратегий каждого участника.

При этом вместо вероятностей p и q использовать площади, отводимые под каждые культуры.

P⁰_i → S⁰_i

q⁰_j → S⁰_j

Применение теории «n» лиц при принятии оптимальных решений

Основные типы взаимоотношений экономических субъектов, базирующихся на теории игр

1. Антагонистические отношения описываются с помощью теории антагонистических игр

2. Отношение 2-х участников с несовпадающими, но не антагонистическими интересами. Эти отношения описываются с помощью биматричных игр.

3. Взаимоотношения «n»-участников, не участвующих в коалициях. Эти отношения описываются с помощью теории «n» лиц (бескоалиционные игры).

4. Взаимоотношения «n»-участников при возможном создании коалиции, описываются с помощью теории коалиционных игр.

Введение в теорию игр «n»-лиц с нулевой суммой

E₁(x,y) = -Е₂(x,у) = E(x,у)

E₁(x,у) + (-Е₂(x,у)) = 0 — отсюда название теории игр с нулевой суммой.

•   Рассматривается игра «n» лиц, где число игроков Y:

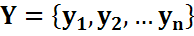
• В качестве участников могут выступать:

• промышленные предприятия

• инвесторов

• кредиторы

• гос. органы

В частности в качестве участников «n» могут выступать различные бизнес-единиц предприятий, которые могут представлять собой центры ответственности прибыли, затрат, инвестиций или их комбинирования.

 Все множество участников У разбивается на 2 подмножества: S и -S.

Участники, принадлежащие «S» представляют одну коалицию, а участники, включенные в «-S» - вторую.

Формально, располагая двумя составными участниками могут рассматривать игру двух лиц с 0-ой суммой.

Пусть V(S) — значения игры для всех участников, принадлежащих S.

V(S) – характеристическая функция игры

Данное разделение на две коалиции позволяет применить теорию 2-х лиц с 0-ой суммой для принятия решений каждой коалицией.

В данном случае выполняются следующие условия:

1. Интересы участников, принадлежащих к той или иной коалиции совпадают.

2. Интересы коалиции являются прямо противоположными, т.е. антагонистическими.

Свойства характеристической функции:

1. V (Ø) = 0

Означает, что коалиция S не имеет участников, выигрыш равен 0.

2. V(-S) = -V(S)

V(S) + V(-S) = 0

3. V(S υ T) ≥ V(S) + V(T) (эффект синергии)

Эффект от объединения больше суммы эффектов, полученных в отдельности.

4. S∩T = Ø

Ø – пустое множество

1. V (Ø) = 0

Означает, что коалиция S не имеет участников, выигрыш равен 0.

2. V(-S) = -V(S)

V(S) + V(-S) = 0

3. V(S υ T) ≥ V(S) + V(T) (эффект синергии)

Эффект от объединения больше суммы эффектов, полученных в отдельности.

4. S∩T = Ø

Ø – пустое множество

Применение теории биматричных игр при условии несовпадения интересов

До сих пор рассматривались ситуации, в которых интересы субъектов экономики, соприкасающихся друг с другом, противоречили.

При этом выигрыш одной стороны автоматически оборачивается проигрышем другой.

Подобные ситуации называются конфликтными, и принятие решения в них основывается на теории игр с нулевой суммой.

Однако на практике подобного рода конфликтные ситуации встречаются довольно редко.

Модель антагонистических игр, изначально создававшаяся для описания конкуренции, для этих целей не подходит.

Конкуренты в большинстве своем стараются не столько навредить сопернику, сколько максимизировать собственную прибыль, которая не равна по модулю с противоположным знаком прибыли конкурента.

Это заставляет для каждого из конкурентов составлять свою матрицу. Отсюда и название математического аппарата: Теория биматричных игр.

Рассмотрим ситуацию:

Пусть имеются два участника, принимающих решения независимо друг от друга.

Первый из них располагает набором стратегий , и оценивает эффективность принимаемых решений по критерию «Э».

Второй располагает набором стратегий , и оценивает эффективность принимаемых решений по критерию «Е».

Рассмотрим ситуацию:

Пусть имеются два участника, принимающих решения независимо друг от друга.

Первый из них располагает набором стратегий , и оценивает эффективность принимаемых решений по критерию «Э».

Второй располагает набором стратегий , и оценивает эффективность принимаемых решений по критерию «Е».

Причем выполняются условия:

Э = ƒ (х, y)

Е = φ (х, y),

Т.е. Э и Е зависят не только от решения, которое принимает участник, использующий данный критерий, но и от решения, которое принимает его противник.

В результате имеем две матрицы:

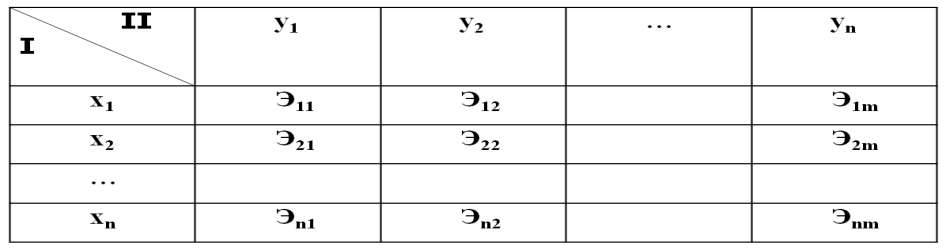
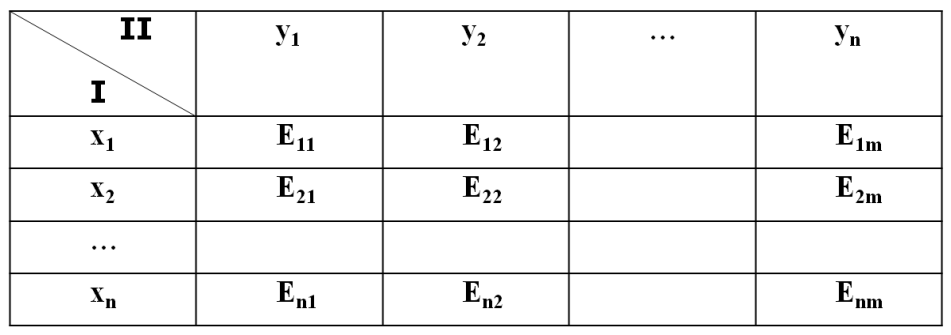
П равилом выбора оптимальных решений в биматричных играх (как и в антагонистических) остается Принцип гарантированного результата. Будем полагать, что обеим сторонам их критерии необходимо максимизировать, тогда:

Как видно, правила отбора для обеих сторон становятся одними и теми же.

Рассмотрим случай, когда первый из субъектов с несовпадающими интересами начинает действовать прежде, чем другой примет решение.

Пусть для определенности первый ничего не знает о стратегии второго, поэтому действовать они будут в условиях неопределенности.

Пусть x_opt=x₂

Второй участник знает, что первый реализует стратегию x₂ и неопределенности уже нет, а есть строка детерминированных значений E₂₁, E₂₂,… E_2m, из которых нужно выбрать максимум, и этот максимум будет соответствовать оптимально стратегии второго участника - y_opt. Однако, между «Э» и «Е» математическая связь неоднозначна и неочевидна. Значит, максимуму E_2j совсем не обязательно соответствует минимум Э_2j – гарантированный результат первого участника. Значит, в отличие от антагонистических игр, в биматричных играх участник, начавший действовать раньше другого, не всегда проигрывает по сравнению со случаем одновременного и независимого принятия решения. Ситуация равновесия в биматричной игре – такая пара смешанных стратегий и , для которой справедливы неравенства:

При любых Означает, что первому участнику биматричной игры не выгодно отклоняться от равновесной стратегии.

При любых q (с вектором)

Означает, что второму участнику биматричной игры не выгодно отклоняться от равновесной стратегии. Сохраняет свою силу в биматричных играх и теория Неймана, т.е. равновесные и смешанные стратегии есть всегда, и они определяются по принципу гарантированного результата. Иногда ситуация равновесия бывает и в чистых стратегиях, но она идеально вписывается в данное выше определение, т.к. чистые стратегии – частный случай смешанных.

Возможности применения теории игр при выборе эффективных решений в экономике

Основные игровые подходы, которые используются при решении экономических задач

В качестве основных теорий находят применение следующие типы игр:

1. Антагонистические игры двух лиц с нулевой суммой

2. Антагонистические игры n-лиц с нулевой суммой

3. Биматричные игры двух лиц с нулевой суммой

4. Кооперативные игры n-лиц.