2.2. Процедура построения разностной схемы

Отметим также, что свести решение ДУ в частных производных к решению систем алгебраических уравнений удается не всегда, а только в случае стационарных процессов (установившихся во времени). При моделировании нестационарных процессов в ДУ появляются члены, зависящие от времени. Методы решения таких задач будут рассмотрены далее.

Рассмотрим процедуру построения разностной схемы на примере следующего уравнения:

д2F	+	д2F	+ e - x	дF	- F = f(x,y)	(1)
дХ2		дY2		дX

в квадрате Р = {0х1; 0 y1} с краевым условием:

(^x, ^y) = exp(^x-^y) (2)

То есть функция F в точках периметра квадрата Р, или, что то же, - в точках краевой линии S, - изменяется по закону (2).

Последовательно находим:

1. Условие (2) позволяет определить функцию f (x,y) во всех точках линии S. Действительно, как бы не изменялась функция F внутри области Р она в точках периметра должна принимать значения, определенные функцией (15), поэтому, подставляя (2) в (1) и проводя дифференцирование, мы получим вид функции f (x,y) в точках на линии S:

f(^x, ^y) = e^{-^y} (e^{^x}+1) (3)

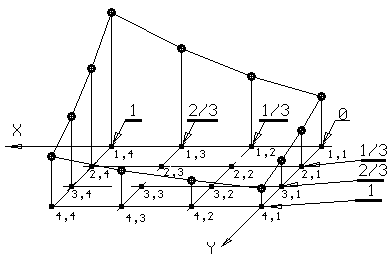
2. Выбираем шаг h=1/3. Перенумеровываем узлы области Р так, как показано на рисунке 2.2.1, и в точках периметра последовательно вычисляем:

Рис.2.2.1

F _1,1 = 1; F _1,2 = exp (1/3) 1,4; F _1,3 = exp (2/3)  1,95;

F _1,4 = exp (1)  2,7; F _2,1 = exp (-1/3) 0,72; F_3,1 = exp (-2/3) 0,51;

F _4,1 = exp (-1)  0,36; F _4,2 = exp (-2/3) 0,51; F _4,3 = exp (-1/3) 0,72;

F _4,4 = 1; F _3,4 = exp (1/3) 1,4; F _2,4 = exp (2/3)  1,95; `

3. Для значений во внутренних узлах согласно (15) составляем систему из 4-х уравнений с четырьмя неизвестными:

F23 – 2F22 + F21	+	F32 – 2F22 + F12	+ e – 1/3	F23– F21	- F22 = e – 1/3 (e 1/3 + 1)
(1/3)2		(1/3)2		(2/3)
F24 – 2F23 + F23	+	F33 – 2F23 + F13	+ e – 2/3	F24– F22	- F23 = e – 1/3 (e 2/3 + 1)
(1/3)2		(1/3)2		(2/3)
F34 – 2F33 + F32	+	F43 – 2F33 + F23	+ e – 2/3	F34– F32	- F33 = e – 2/3 (e 2/3 + 1)
(1/3)2		(1/3)2		(2/3)
F33 – 2F32 + F31	+	F42 – 2F32 + F22	+ e – 1/3	F33– F31	- F32 = e – 2/3 (e 2/3 + 1)
(1/3)2		(1/3)2		(2/3)

Введем для краткости обозначения: F_2,2  x, F_2,3  y, F_3,2  z, F_3,3  u. Подставляя их в полученную систему и проводя предварительные вычисления, получим следующую систему линейных уравнений:

–37x + 10,1y +9z = –16,5

+8,2x –37y +9u = –35,45

+9y +8,2z – 37u = –18,7

+9x – 37z + 10,1u = –7,42

Программа вычисления корней данной системы приведена ниже:

uses crt; const n=4;

type qw=array[1..n,1..n] of real; Linia=array[1..n]of real;

const MotL:qw= ((-37,10.1,9,0),(8.2,-37,0,9),

(0,9,8.2,-37),(9,0,-37,10.1));

BotL:Linia= (-16.5,-35.45,-18.7,-7.42);

var m1,m2:qw; x,b1,b2:Linia; aa,ss,zz:real;i,j,k,q,tt:integer;

Procedure CoeFA(i,j,k:byte);

begin m2[i,j]:=m1[i,j] - m1[i,k]*m1[k,j]/m1[k,k] End;

Procedure FreeB(i,k:byte);begin b2[i]:=b1[i]-b1[k]*m1[i,k]/m1[k,k] End;

BEGIN

clrscr; For i:=1 To n Do x[i]:=0; For i:=1 to n Do b1[i]:=BotL[i];

For i:=1 to n Do For j:=1 To n Do m1[i,j]:=MotL[i,j];

For i:=1 to n Do For j:=1 to n Do m2[i,j]:=0;

For j:=1 to n Do m2[1,j]:=m1[1,j]; b2[1]:=b1[1];

For tt:=2 To n Do

Begin For i:=tt to n Do m2[i,tt]:=0;

For i:=tt To n Do For j:=2 to n Do CoeFA(i,j,tt-1);

For i:=tt to n Do FreeB(i,tt-1);

For i:=1 to n Do For j:=1 To n Do m1[i,j]:=m2[i,j];

For i:=1 to n Do b1[i]:=b2[i];

End;

zz:=0; X[n]:=b2[n]/m2[n,n];

For i:=n-1 DownTo 1 Do

Begin zz:=b2[i]; q:=n;

For j:=i To n-1 Do Begin zz:=zz-m2[i,q]*x[q]; dec(q); End;

x[i]:=zz/m2[i,i]; End;

For i:=1 to n Do WriteLn('X',i,'=',X[i]:6:4); Repeat Until KeyPressed;

END.

Система имеет следующее решение:

F_2,2  x=1.0119; F_2,3  y=1,4288; F_3,2  z=0,7233; F_3,3  u=1,0133.

Пример. Рассчитать собственные частоты колебаний балки с шарнирно-закрепленными концами, показанной на рис.2.2.2.

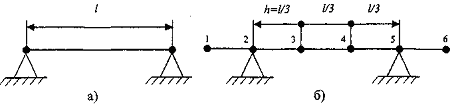
Рис.2.2.2. балка (а) и ее расчетная модель (б)

Уравнение свободных колебаний балки имеет вид

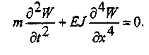
Примем массу балки сосредоточенной в узлах 3,4 - и напишем уравнения их движения в конечных разностях. Считая, что свободные колебания балки происходят по гармоническому закону , общее уравнение преобразуем к виду

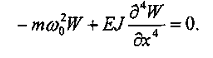
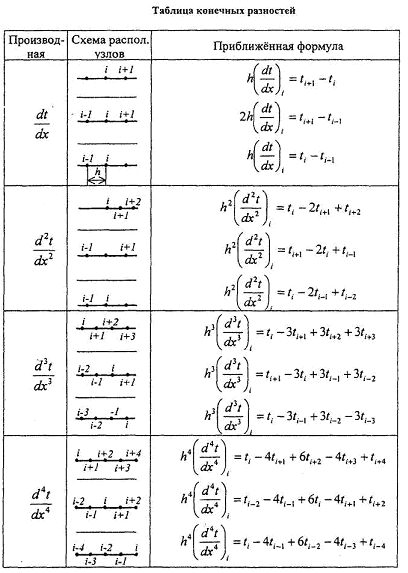
Подставляя в него вместо частной производной выражение в конечных разностях, для точки 3 получим:

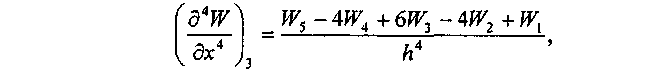
где h=l/3, или после подставления

где

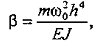
У рассматриваемой балки прогибы в точках 2 и 5 равны 0, т.е. W₂=Ws=0. Отсюда получим

Рассуждая аналогично, для точки 4 получим

В данных уравнениях присутствуют прогибы в условных точках 1 и 6. Они могут быть найдены на основе разложения функции в этих точках в ряд Тейлора

Пренебрегая всеми членами разложения, начиная с третьего члена, ввиду их малости, для точки 1 получим

Так как Wi = 0, окончательно получим W\ — - W-$ Для точки 6 запишем

Далее получаем систему уравнений:

Для решения этой системы составим определитель

Раскрывая его, получим уравнение (5- β)² -16=0. Откуда найдем (β1=1 и (β1⁼9). Преобразуем выражение (4.4) к виду

найдем

Для сравнения точный расчет аналитическим методом дает вместо 9 и 27 значения 9,86 и 39,4. Такое большое расхождение, особенно по второй частоте, можно объяснить разбиением балки всего на три участка. Обычно' рекомендуется не меньше десяти.

Составление конечно - разностных уравнений конструкций типа плат. Уравнение свободных колебаний пластины имеет вид:

Представляя решение в виде W=W(x,y,t)=W(x,y)<F* и используя данные таблицы (приведенной выше), слагаемые уравнения для некоторой точки г на рис.2.2.3 представим в виде :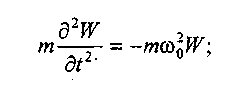

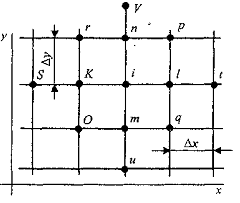
Рис.2.2.3 Фрагмент сетки.

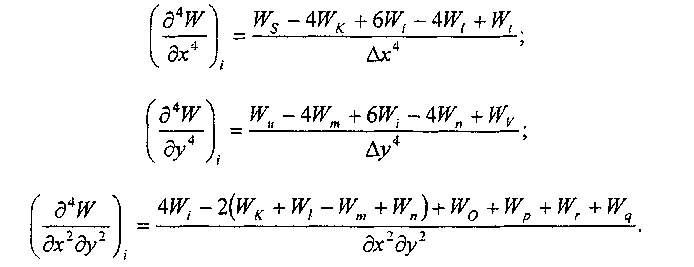
Подставляя найденные выражения в уравнение свободных колебаний и считая Ах = Ду, получим уравнение:

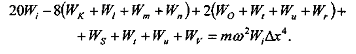
Для прямоугольной пластины, жестко защемленной по контуру, уравнение справедливо для точек 17,18,19,24 - 36,31 - 33 на рис.2.2.2.

В остальных точках появляются известные контурные значения прогиба (они равны нулю) и законтурные неизвестные значения.

Применяя разложение функции в ряд Тейлора, для точки О получим:

Используя разностные представления

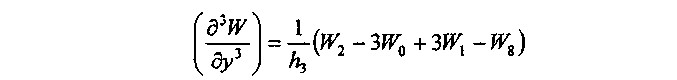
и замечая, что для пластины, жестко закрепленной по контуру, граничные условия равны нулю, из уравнения (4.9) получим

Отсюда Полученную зависимость можно использовать для исключения лишних неизвестных при записи разностных уравнений.

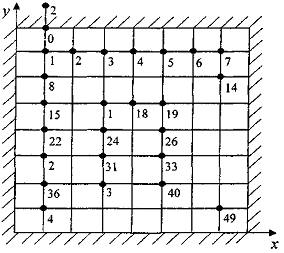
Рис.2.2.4. Плата, защемленная по контуру.

Например, для узла 15 получим

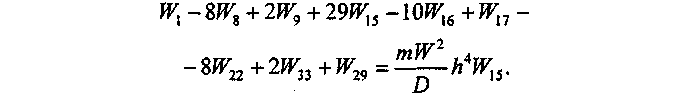
Таким образом, получим систему из 49 алгебраических уравнений, которая может быть решена различными методами. Наиболее часто применяется метод Гаусса, называемый также методом последовательного исключения переменных.

Рассмотренная схема решения является неявной. Может применяться и явная схема, когда частная производная заменяется также конечными разностями, а затем решение идет на каждом шаге с интервалом.