2.4.3. Моделирование на эвм тепловых процессов контактных соединений

Поставим задачу исследования на ЭВМ нестационарного процесса нагрева электрорадиоэлементов (ЭРЭ) при пайке выводов методом конечных разностей. Данная задача имеет практический смысл, поскольку современные ЭРЭ и особенно интегральные полупроводниковые микросхемы весьма чувствительны к воздействию высоких температур, причем ЭРЭ могут подвергаться нагреву многократно (пайка). Последнее обстоятельство приводит к необратимым изменениям электрических параметров и характеристик изделий. Таким образом, возникает следующая задача учета температурных режимов ЭРЭ при изготовлении и эксплуатации: обеспечить температурный режим нагрева ЭРЭ, при котором температурное поле не превышало предельно допустимых норм по ТЗ.

Исследования показывают, что воздействие t⁰ при пайке аналогично термоудару на ЭРЭ, последствия которого (отслаивание подложки, нарушение герметичности корпуса и др.) не проявляются сразу при монтаже аппаратуры, а являются причиной ее отказа при эксплуатации. Отсюда следует, что обеспечение нормального теплового режима пайки имеет важное значения для обеспечения надежности всей аппаратуры.

Основными параметрами пайки является температура пайки Т_П, время пайки t_П, температура нагрева прибора Т_Н и расстояние от корпуса прибора до места пайки L.

Нагрев ЭРЭ в результате пайки представляет сложный процесс передачи тепловой энергии от места пайки к корпусу ЭРЭ, в котором участвуют все виды передачи тепла: кондуктивный теплообмен по выводу, излучение и конвективный теплообмен поверхностей ЭРЭ и выводов с окружающей средой. Сам процесс является нестационарным, так как за время пайки происходят изменения температуры в различных точках изделия. Подобные задачи на практике решаются с использованием различных допущений и идеализаций.

Электронный прибор представляют в виде стержня, на одном конце которого расположен источник постоянной температуры (место пайки), а на другом - конструктивно связанная со стержнем фиктивная масса (ФМ). Эта ФМ представляет собой математическую модель реального электронного прибора, обладающую адекватными прибору теплофизическими параметрами: теплоемкостью и теплоотдачей в окружающую среду. Геометрически ФМ можно представить в виде тонкого диска, размещенного на торце внешнего вывода. Теплопроводность ФМ (массивного элемента МЭМС) считается бесконечно большой, то есть температура ФМ во всех ее точках одинакова.

Нагрев ФМ аналогичен нагреву элемента МЭМС в интересующей точке (например, в месте крепления полупроводникового кристалла в корпусе). Сказанное позволяет свести задачу математического моделирования процесса нагревания элемента МЭМС при пайке к задаче определения температуры ФМ, если сделать следующие предположения:

Рис.2.4.1.

• нагрев ФМ равномерен в каждый момент времени;

• конец вывода в месте пайки мгновенно достигаем температуры пайки и сохраняет его в течении всего процесса;

• тепловые коэффициенты не зависят от температуры;

• конвективный обмен вывода с окружающей средой пренебрежимо мал.

При таких допущениях тепловой процесс пайки представим с помощью двух ДУ:

S	дТ	- АТ = Е		дТ
	дХ			дt
	д2Т	= C	дТ		1
	дХ2		дt

где: S – площадь сечения вывода ЭРЭ (S = 10^–6м² –далее в скобках приводятся типичные значения параметров, используемые далее в примере расчета температурного поля вывода при его пайке);

 – коэффициент теплопроводности материала вывода радиоэлемента (=400 Дж/мс^оК);

T – температура ФМ;6

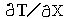
– изменение температуры на границе вывода и корпуса ЭРЭ;

А – суммарный коэффициент теплоотдачи ЭРЭ в окружающую среду (А=0,5 Дж/(с^оК) );

Е – теплоемкость фиктивной массы (Е=0,05 Дж/^оК);

С– удельная теплоемкость материала вывода (С=410⁶ Дж/(м³^оК);

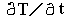
– скорость изменения температуры ФМ;

X – расстояние от места пайки;

t – время пайки.

Нагрев ФМ в различные моменты времени получается решением уравнения 1. В нем уменьшаемое и вычитаемое в левой части характеризует подвод тепла к ЭРЭ через вывод и теплоотдачу ЭРЭ в окружающую среду, а правая часть – описывает нагрев ЭРЭ в процессе пайки.

Уравнение (8.2) определяет передачу тепла через вывод ЭРЭ. В нем левая часть задает тепловой поток через вывод, а правая – нагрев вывода.

Начальным условием обоих уравнений является температура вывода и ЭРЭ в нулевой момент времени начала пайки:

T(X,0) = 293^OK (20^OC)

Граничным условием на (левом) конце вывода является температура пайки:

T(0,t) = Т_П

Для решения уравнений (8.1) и (8.2), относящихся к классу линейных ДУ (1- уравнение первого рода и 2- параболическое уравнение) разделим вывод элемента поперечными сечениями с шагом h (рисунок 2.4.2) и на временной оси отметим моменты времени Тj=j где: – интервал времени, j – индекс ( j=0 в начальный момент пайки).

,

Рис. 2.4.2.

Температура вывода в i–м сечении в j-й интервал времени от начала пайки:

T_ij = T ( ih, j )

Можно записать следующие выражения перехода от частных производных к конечным разностям в соответствии с принятыми обозначениями:

дТij		Тij- Тi-1,j	;	дТij		Тij- Тi-1,j
дХ		h		дt		

Аналогичный переход от второй производной к конечным разностям даст:

д2Тij		Тi+1,j- 2Т1j + Тi-1,j
дХ2		h2

Заменим в уравнении (8.1) производные конечными разностями, получим:

S	Тn,j- Тn-1,j	- AТn,j = СФМ	Тn,j+1 - Тn,j
	h		

Отсюда следует, что в момент времени t=(j+1) температура ФМ составит:

Тn,j+1 = {	S	-	A	+1} -	СФМ 	Тn-1,j
	hСФМ		СФМ		hСФМ

Заменим вторые производные конечными разностями:

	Тi+1,j–2Тi,j+Тi-1,j	= C	Тi+1,j–Тi,j
	hСФМ		

Пусть  =(/h²C). Можно показать, что условие устойчивости решения, то есть возможность получения точных решений за определенное количество шагов, примет вид:

	h2C	=	1	 
	2		2

Далее примем =0.2/. Тогда значение рабочей температуры в момент времени t=(j+1) в i –м сечении стержня примет вид:

Ti,j+1 = 0.2Ti+1,j +(1-0,4)Ti,j+ 0.2Ti-1,j

По приведенным формулам можно рассчитать температуру ФМ в сечениях вывода последовательно в моменты времени t_j = 0, t_j+1 = , t_j+2 = 2, … . В общем случае, в произвольный k-й момент времени t_k = (t_k-1 + ). Программа на языке Паскаль вычисления температурного поля в стержне методом конечных разностей (МКР), может иметь следующий вид:

Uses crt;

Const n=15;

Type mass=array[1..n]of word;

Var Md,Mt:mass; i,t:integer; b:boolean;

Begin

Clrscr; t:=0; b:=false;

For i:=1 to n Do Mt[i]:=293; Mt[1]:=600;

For i:=1 to n Do MD[i]:=0;

Repeat

For i:=2 to n-1 Do

Md[i]:=Round(0.2*(Mt[i+1]+Mt[i-1])+0.6*Mt[i]);

If Md[2]=Mt[2] then b:=true;

t:=t+1;

For i:=2 to n-1 Do Mt[i]:=Md[i];

Until b;

For i:=1 to n Do Write(Mt[i],’ ’);

End.

Аналогичным образом может быть составлена программа, реализующая вычисление значений температуры в дискретные моменты времени в последнем n-м сечении стержня, к которому подсоединена фиктивная масса.

Ошибки ограничения уменьшаются при h  0 и   0, то есть решение разностных уравнений асимптотически приближается или сходится к решению ДУ. Следовательно, с точки зрения повышения точности решений следует уменьшать шаг дискретизации по длине и по времени, что, в свою очередь, ведет к возрастанию количества основных циклов в алгоритме вычислений (пропорционально m x n), то есть – к увеличению времени счета.

Другим важным свойством МКР является устойчивость решений. Устойчивость метода означает, что любые ошибки (округления или ограничения) не возрастают в ходе вычисления решения. Доказано, что указанный процесс сходится и устойчив, если (<0.5) или (<1/[2]). Тем самым накладываются ограничения на выбор шага  по времени при выбранном шаге h разбиения вывода сечениями.

Преимущества метода: (а) метод универсален и пригоден для области любой формы, причем источники тепла могут располагаться произвольно; (б) в задаче можно задавать любые граничные и начальные условия – алгоритм решения от этого не меняется; (в) в процессе решения получается полная картина распределения температуры внутри области на каждом шаге по времени, то есть возможен контроль допустимых температур; (г) возможно совершенствование и усложнение модели для получения более точной картины тепловых явлений.

Практическое задание:

Исследовать процесс нагрева элемента при пайке его выводов

1. Составить программу вычисления значений температуры в дискретные моменты времени в последнем n-м сечении стержня.

2. Построить график изменения температуры вдоль стержня в момент достижения фиктивной массой температуры 400^ОС

3. Принять параметры модели пайки:

N п/п	Параметр	Значение
1	Темпеатура паяльника (ТП)	550оК
2	Число дискрет (n)	15
3	Площадь сечения вывода (S)	10–6м2
4	Коэффициент теплоотдачи (А)	0,5 Дж/(соК)
5	Коэффициент теплопроводности вывода ()	400 Дж/мсоК
6	Теплоемкость фиктивной массы (CФМ)	0,05 Дж/оК
7	Удельная теплоемкость материала вывода (С)	4106 Дж/(м3оК)