2.4.2. Уравнение теплопроводности Фурье для дискретной модели блока

Выразим плотности потоков J [Дж/м²с] через температуру в узлах сетки. С этой целью воспользуемся гипотезой о линейности свойств среды – законом Фурье. Этот закон говорит о том, что плотность теплового потока между двумя узлами пропорциональна разности температур между этими узлами и обратно пропорциональна расстоянию между ними, например:

JX+ = K	ti+1,j,k – ti,j,k	(17)
	hX

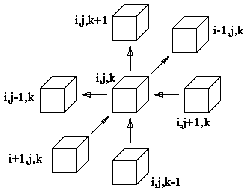
Коэффициентом пропорциональности здесь служит коэффициент теплопроводности К [Дж/мс^ОK]. Рассмотрим элемент разбиения блока с номером (i, j, k) и все элементы, имеющие общие с ним грани (рисунок 2.4.1). На рисунке 2.4.1. стрелками показаны направления передачи тепла между элементами. Запишем уравнения для плотности всех шести потоков, входящих в уравнение теплового баланса:

Рис.2.4.1.

JX+ = K	ti+1,j,k – ti,j,k	;	JX- = K	ti1,j,k – ti+1,j,k
	hX			hX
JY+ = K	ti,j+1,k – ti,j,k	;	JX- = K	ti1,j,k – ti,j+1,k
	hY			hY
JZ+ = K	ti,j,k+1 – ti,j,k	;	JX- = K	ti1,j,k – ti,j,k+1
	hZ			hZ

Если теперь подставить значения плотности потоков в уравнение (16), то получим известное уравнение теплопроводности Фурье. Используя соотношения, полученные ранее и переходя к дифференциальной форме можно записать:

K(	д2	+	д2	+	д2	) + Q = CУД	д
	дX		дY		дZ		дt

где: С_УД – удельная теплоемкость элемента [Дж/м^{3 О}К]. Отсюда уравнение Фурье в дифференциальной форме мы получим заменой типа:

ti+1,j,k - ti,j,k		-	ti,j,k - ti+1,j,k		
hX			hX			д2
	hX					дX2

Уравнение в конечных разностях составляется для всех элементов блока. Плотность потока на поверхности определяется из предположения, что потоки на границах блока пропорциональны перепаду температур на некотором расстоянии (равном h_X) и, что температура за пределами блока =const.Это может быть при охлаждении блока путем принудительного обдува воздухом постоянной температуры. Итак, плотность потока на границе с нормалью к Х равна:

J⁺_X = K_T(^t_H – ^t_(lx/hx),j,k)/h_X

Величина К_Т здесь имеет смысл коэффициента теплопроводности, представляющего среднюю теплопроводность интервала, в который входит граница блока. Шаг h_X введен в выражение (18) искусственно для того, чтобы определеить положение точки за контурами, в которой температура считается известной. Этот шаг можно взять таким же, как и внутри блока. При экспериментальном изучении теплопроводящих свойств границы раздела определяют отношение К_Т/h_X, которое называется коэффициентом теплообмена

Разделим уравнение на c, умножим на  и введем новые обозначения:

J	+		= I	+	;	J	-		= I	-
	x	chX		x			x	chX		x
J	+		= I	+	;	J	-		= I	-
	y	chY		y			y	chY		y
J	+		= I	+	;	J	-		= I	-
	z	chZ		z			z	chZ		z

Введем также новое обозначение для удельного тепловыделения:

Q = g	
	c

В новых обозначениях уравнение (16) примет вид:

I X+ – I X+ + I Y+ – I Y+ + I Z+ – I Z+ + Q = t+1 – t

Таким образом, и плотности потоков и удельное тепловыделение имеют одну размерность – температуры и будут величинами одного порядка. Введя коэффициенты:

AX = g	K	; AY = g	K	; AZ = g	K
	chX		chY		chZ

Мы можем записать:

I_X⁺ = A_X [ ^t_i+1,j,k – ^t_i,j,k] ; I_X^– = A_X [  ^t_i,j,k–  ^t_i-1,j,k] ;

I_Y⁺ = A_Y [ ^t_i,j+1,k – ^t_i,j,k] ; I_Y^– = A_Y [  ^t_i,j,k–  ^t_i,j-1,k] ;

I_Z⁺ = A_Z [ ^t_i,j,k+1 – ^t_i,j,k] ; I_Z^– = A_Z [  ^t_i,j,k–  ^t_i,j,k-1] .

Решение системы уравнений можно находить следующим образом:

1. Определяем температуру в узле через один шаг  по времени:

   t+1i,j,k = I X+ – I X– + I Y+ – I Y– + I Z+ – I Z– + Q +  ti,j,k

2. Вычисление по (21) выполняем для всех узлов.

3. Определяем температуру в узлах в момент 2 и так далее.

Если в результате такого расчета разность ^t+1 – ^t будет постепенно уменьшаться и температура стабилизироваться, то решение считается устойчивым. Если же разность ^t+1 – ^t во всех или некоторых узлах не будет уменьшаться по времени, то решение – не устойчиво.